Поля. Алгебраические операции для элементов поля. Комплексное число. Алгебраическая форма записи комплексного числа, страница 3

6.  Если некоторый столбец определителя состоит из нулей Dj(θ)=θ.

7.  Инвариантность определителя к линейной комбинации столбцов. Определитель не изменится, если к элементам одного из его столбцов прибавить соответственно элементы другого столбца, умножив на фиксированное число.

8.  det (λA)= λⁿdet(A)

Алгебраические дополнения и миноры. Рассмотрим произвольный (например j-ый) столбец определителя D.

. Соберем в правой части суммы все слагаемые, содержащие α_1j,α_2j,…,α_nj, и вынесем эти элементы за скобку

= 

(*) A_ij – некоторая сумма (алгебраическое дополнение элемента ij из D).

det

det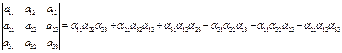 

Аналогично выводится формула разложения определителя по элементам строки.

D= α_i1A_i1+…+α_inA_in (**)

Таким образом мы доказали следующую теорему 1.

Теорема 1. Сумма всех произведений элементов какого-либо столбца (строки) определителя D на соответствующее алгебраическое дополнение равна самому определителю D.

Теорема2.  Сумма всех произведений элементов какого-либо столбца (строки) определителя D на соответствующее алгебраическое дополнения элементов другого столбца (строки) равно нулю.

Def: Если в матрице n порядка удалить i строку и j столбец, то оставшиеся элементы образуют некую матрицу (n-1) порядка, определитель которой называется минором и обозначается M_ij

Теорема 3. A_ij=(-1)^i+j * M_ij

Разложение по строке:

Разложение по столбцу:

Выберем в матрице n-го порядка произвольно к строк и к столбцов. Элементы, которые стоят на пересечении этих строк и столбцов, образуют квадратную матрицу к-ого порядка. Её определитель назовем минором к-ого порядка и обозначим , где i₁…i_k – номера выделенных строк. Если зачеркнуть в исходной матрице выбранные строки и столбцы, то получим квадратную матрицу (n-k) порядка. Берем определитель , назовем его дополнительным минором m и обозначим его (индексы соответствующих зачеркнутых строк / столбцов).

Теорема Лапласа.

(1≤j₁≤j₂≤…≤j_k<n), где i=i₁+…+i_k. j= j₁+…+j_k

Используя теорему Лапласа можно доказать мультипликативное свойство определителя. Если надо найти определитель AB, то  det(AB)=detA*debt

(1)Σ произведений эл. к.-л. столбца(стр.)на алгебраическое дополнение зл. др. столбца(стр.) =0.

(1)Д-во: заменим правой и левой частям рав-ва(*)(см. выше) эл. α_1j, α_2j…α_nj, на соответствующ. эл. к.-л. др., например, k – того столбца, тогда опред-ель слева соотнош. (*) будет иметь 2 одинак. столбца и по св-ву 3 будет=0, т.е. при k≠j, α_1kA_1j+α_2kA_2j+…+α_nkA_nj=0.

(2)Алгебраическое дополнение A_ij элемента α_ik связано с минором M_ij соотношением A_ij=(-1)^i+j * M_ij

(2)Док-во: пусть i=j=1 , соберем в правой части рав-ва, все члены с α₁₁ и вынесем α_1j за скобку и получим ; запишем опред. матриц, получ. из исходной, после вычеркивания перв. стр. и перв. столбца ; N(1, i₂…i_n)=N(i₂…i_n); если i и j произвольны, переведем путем последов. перестановки соседних строк и столбцов эл. α_ij в лев. верхн. угол матрицы; (i+1)+(j+1)=i+j-2; A_ij=(-1)^i+j-2*M_ij=(-1)^i+j*M_ij;

Формулы Крамера.

Пусть имеется однородная система уравнений Ax=b, b≠0, detA≠0.

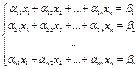 Домножим систему на А, где А – матрица с элементами α. X- неизвестная матрица. 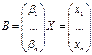. Получаем (α₁₁A₁₁+α₂₁A­₂₁+…+α_n1A_n1)x₁+… +(α_1nA₁₁+α_2nA₂₁+…+α_nnA_n1)x_n=β₁A₁₁+…+β_nA_n1

Таким образом по теоремам 1,2 имеем detA*x₁ + 0*x₂+…+0*x_n=detA_1­­, где А1 – матрица полученная из исходной заменой 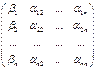Значит . Следовательно j=1..n

Обратные матрицы

Пусть А – произвольная матрица размером mxn. С некоторым detA≠0. Тогда А-невырожденная или неособенная (в случае detA=0 матрица называется вырожденной или особенной), составляет присоединенную или союзную матрицу В к матрице А.

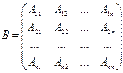. В i-той строке матрицы B находятся алгебраические дополнения к элементам i-ого столбца матрицы А.

Вычислим АВ..

Воспользуемся мультипликативным свойством. det(AB) = detA*detB=(detA)ⁿ=BA. Т.к. матрица А невырождена, то detB=(detA)^n-1.

Def: A^-1 называется обратной матрице А, если она удовлетворяет условию А*А^-1=А^-1*А=I