Математика \ Геометрия и алгебра

Поля. Алгебраические операции для элементов поля. Комплексное число. Алгебраическая форма записи комплексного числа, страница 4

Подчеркнём, что обратная матрица $ для невырожденных матриц и находится по формуле 

Не существует матрицы, обладающей свойством: det(ΑA-1)=detA det(A-1)= =detI=1

 

(A-1)-1=A; (AB)-1=B-1A-1; (AB)(B-1A-1)A(BB-1)A-1/I= AA-1=I;

Используя обратную матрицу можно находить решение СЛАУ Ax=b с невырожденной матрицей. x=(A-1)b

Степени матрицы

1.  A1=A; A0=I

2.  A2=Α

3.  A-m=A-1…A-1

4.  A-m=(A-1)m=(Am)-1

5.  Ap+q=ApAq

Def: Матрица А и В называются перестановочными, если АВ=ВА. Степени одной и той же матрицы перестановочны.

Def: Матрица АТ размера nxm называется транспонированной по отношению к матрице А, размером mxn. [AT]ij=[A]ji

Свойства транспонированных матриц:

1.  Если две матрицы А и В размера mxn, то (αA+βB)T=αAT+βBT

2.  Если Аmxn, Bnxk (AB)T=BTAT

3.  Если А – квадратная матрица, то (A-1)T=(AT)-1

Def: Если А = АТ, то матрица А называется симметрической (симметричной), если А=-АТ, то матрица А называется кососимметрической.

Свойства

1)  Если А и В симметричные матрицы, то матрица А+В тоже симметричная

2)  АВ может не быть симметричной матрицей

3)  Полиномы от симметричных матриц есть симметричные матрицы.

Ортогональные матрицы

Матрица А называется ортогональной, если ААТ=АТА=I

Для любой ортогональной матрицы определитель равен +1.

Свойства:

1)  Если А- ортогональная матрица, то А-1 – ортогональная матрица.

2)  Произведение ортогональных матриц есть ортогональная матрица.

Def: Заменим все элементы матрицы А сопряженными, получим матрицу , называемую комплексно-сопряженной с А.

Свойства:

1)

2)

3)

4)

Def: Матрицы А и называются эрмитово-сопряженными

Def: Если А= (А=А*), то матрица А называется эрмитовой матрицей.

Def: Если А=-А*, то А называется эрмитовокососимметричной.

Def: Если ΑA*=A*A=I, то А-унитарная матрица.

Свойства унитарных матриц:

1)  Матрица обратная к унитарной является унитарной.

2)  Произведение унитарных матриц – унитарная матрица

3)  Модуль определителя унитарной матрицы равен 1

Клеточные матрицы

Матрица вида 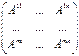 называется клеточной матрицей (разбитой на клетки/блоки)

Операции над клеточными матрицами выполняются формально по тем же правилам, что и над обычными.

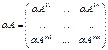
1)  Пусть 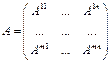 и 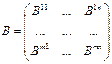, размеры которых одинаковы, то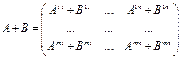

2)  Умножение аналогично стандартному, с учетом того, что соответствующие клетки можно перемножать.

Def: Клеточная матрица вида 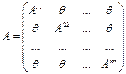называется квазидиагональной или клеточнодиагональной. Сумма и произведение квазидиагональных матриц также является квазидиагональной матрицей

Определение линейного пространства. Свойства линейных пространств и примеры линейных пространств

Линейным (или векторным) пространством на поле F называется множество элементов (векторов), которые удовлетворяют следующим аксиомам:

L={x; y; z}

A) Каждой (x,y)ÎL ставится в соответствие элемент этого множества, называемый суммой элементов x и y (x+y) и обозначается z

1. x+y=y+x=z

2. (x+y)+z=x+(y+z)

3. $ qÎL: "xÎL: x+q = x

4. "xÎL: $ (-x)ÎL   x + (-x) = q

B) Каждой паре aÎF, xÎL отвечает единственный элемент этого множества, называемый произведением числа a*x и обозначается a=ax

1. δ(jx) =(δj)x   "δ,jÎF, "xÎL

2. 1*x = x   "xÎL

C) Операции сложения и умножения связаны между собой отношениями:

1. a(x+y) = ax+ay   "aÎF, "x,yÎL

2. (a+λ)x = ax+λx   "λ,aÎF, "xÎL

Из аксиом 1-8 можно вывести следующие свойства линейных пространств:

1)  В линейном пространстве $ единственный нулевой элемент

2)  В линейном пространстве для каждого элемента x $ единственный противоположный элемент (-x)

3)  Для всякого xÎL справедливо равенство q x = q

4)  Для всякого xÎL в любом линейном пространстве противоположным элементом служит: y=(-1)*x

Замечание:

Наличие противоположного элемента позволяет ввести операцию вычитания

x-y = x+(-y)

5)  -a*x = (-a)*x = a*(-x)

Скачать файл