баллах. Максимальное расчетное землетрясение (МРЗ) - землетрясение со средней повторяемостью до 10000 лет. Проектное землетрясение (ПЗ) – со средней повторяемостью до 100 лет.
Расчет на сейсмическое воздействие проводится для площадок с сейсмичностью
более 4 баллов. При сейсмичности в 4 балла – согласно решению проектной (конструкторской) организации. Исходными данными являются воздействия от землетрясений (МРЗ и ПЗ), задаваемые в виде акселерограмм и спектров ответа для трех направлений (вертикального и двух горизонтальных).
Относительное демпфирование принимается равным 0,02. При наличии экспериментального обоснования допускается использование других значений.
Если доминирающая частота (n1) более 20гц, расчет допускается проводить в статической постановке с умножением ускорений, полученных по спектру ответа, на 1,3 для n1 = 20…33гц, и на 1,0 для n1 > 33гц.
Определение напряжений и деформаций допускается проводить в предположении статического воздействия найденных расчетом амплитудных значений сейсмических нагрузок.
8.1. Математическое моделирование динамического отклика сложных конструкций на произвольное возмущение.
Достоинство МКЭ заключается прежде всего в том, что этот метод позволяет достаточно детально учесть жесткостные, массовые и кинематические особенности рассчитываемой системы, что обеспечивается соответствующим формированием матриц жесткости [K], массы [M] и диссипации [H]. Особенности формирования этих матриц описаны в [3].
Расчет отклика сложной системы на произвольное воздействие заключается в решении системы дифференциальных уравнений движения, порядок которой определяется числом степеней свободы. Матричная запись такой системы для момента времени t+dt имеет вид
[M]![]() , (8.1.1)
, (8.1.1)
где: [H] – матрица диссипации – определяется через экспериментальные коэффициенты a и b как
[H] = a![]() b
b![]() .
.
В случае отсутствия опытных данных она может быть приближенно определена по формуле [7]
[H]
= (0,1…0,2)![]() n
n![]()
в которой n - низшая собственная частота системы;
{P![]() } – столбец
обобщенных внешних сил, закон изменения которых может быть произвольным.
} – столбец
обобщенных внешних сил, закон изменения которых может быть произвольным.
Принимая линейный закон изменения ускорения в течение малого промежутка
времени dt (dt![]() , где Т – период собственных
колебаний на той частоте, влияние которой и всех предыдущих необходимо учесть),
запишем (см. рис.19):
, где Т – период собственных
колебаний на той частоте, влияние которой и всех предыдущих необходимо учесть),
запишем (см. рис.19):
{![]()
![]() }
= {
}
= {![]() } +
} + 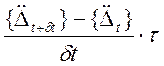 (8.1.2)
(8.1.2)
Перепишем выражение (8.1.2) в виде
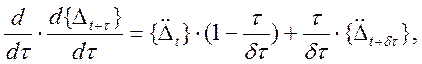
интегрируя которое с учетом граничных условий (С1ô![]() = {
= {![]() }), получим
}), получим
{![]() } = {
} = {![]() }
}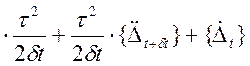 .
.
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
t t+![]() t
t
Рис.20
Вновь интегрируя последнее соотношение и учитывая, что С![]() ô
ô![]() ={
={![]() }, получим
}, получим
{![]() } = {
} = {![]() }+{
}+{![]() }
}![]() +{
+{![]() }
}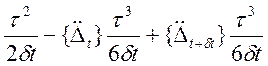 .
.
Окончательно
для момента времени ![]() , имеем:
, имеем:
{![]() } = {
} = {![]() }+{
}+{![]() }
}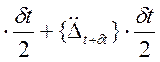 (8.1.3)
(8.1.3)
{![]() } = {
} = {![]() }+{
}+{![]() }
}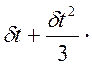 ({
({![]() }+{
}+{![]() }) (8.1.4)
}) (8.1.4)
Из (1.11) столбец ускорений в конце временного интервала будет
{![]() } =
} = 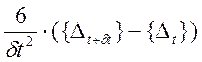 -
- 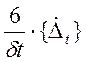 - 2{
- 2{![]() } (8.1.5)
} (8.1.5)
После подстановки (8.1.5) и (8.1.3) в (8.1.1), разрешающая система будет иметь вид:
[(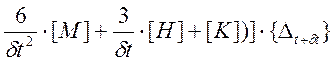 = {{P
= {{P![]() }+[M]
}+[M]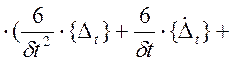
+2{![]() })
+ [H]
})
+ [H]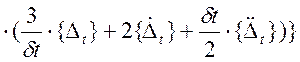 ,
,
или [![]() ]
]![]() = {
= {![]() } (8.1.6)
} (8.1.6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.