Системи звичайних диференціальних рівнянь. Теорія лінійних систем, страница 3

у якому точка, що рухається, у заданий момент  часу перебувала б у заданій точці фазового  простору , тобто задовольняла б початковим умовам (1.14).

Питання існування й одиничності розв'язання задачі Коші для нормальної системи (1.4) вирішує наступна теорема:

Нехай дана нормальна система:

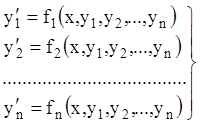                                                     (1.16)

і поставлені початкові умови:

, , ..., .                                 (1.17)

Припустимо, що функції  , що стоять у правих частинах системи (1.16) визначені в деякій замкнутій обмеженій області :

,   

з точкою  усередині області  й задовольняють у цій області наступним умовам:

1) неперервні по всіх своїх аргументах й, отже, обмежені в , тобто:

,

де , ;

2) задовольняють умові Ліпшица по аргументах , тобто:

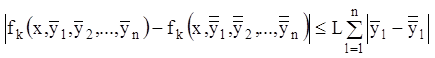,                           (1.18)

де  – постійна Ліпшица , а  й  – дві будь-які крапки області .

При цих припущеннях система (1.16) має єдине розв'язання

, , ..., ,

задовольняюче початковим умовам (1.17). Це розв'язання свідомо визначене й неперервне диференційоване в інтервалі:

,                                                            (1.19)

де

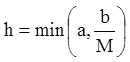.                                                          (1.20)

Зауваження: з теореми витікає, що якщо праві частини системи (1.16), наприклад, поліноми від своїх аргументів, то для будь-яких початкових умов (1.17) існує єдиний розв'язок системи (1.16).

1.4 Розв’язання системи диференціальних рівнянь.

Інтеграл нормальної системи. Число незалежних інтегралів

Означення: Сукупність  функцій

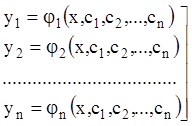,                                                        (1.21)

визначених у деякій області зміни змінних , що мають неперервні часткові похідні по , будемо називати загальним розв'язанням системи (1.16) в області , якщо:

1) система (1.21) розв'язна щодо довільних постійних  в області , тобто для будь-якої точки  системою (1.21) визначаються значення :

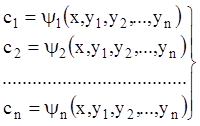;                                                        (1.22)

2) сукупність (1.21) є розв'язанням системи (1.16) при будь-яких значеннях , одержуваних з формул (1.22), коли точка  пробігає область .

Формула загального розв'язання (1.21) дає можливість вирішити будь-яку задачу Коші для системи (1.16) при будь-яких початкових умовах (1.17), аби тільки точка  належала області . Справді, підставляючи (1.17) в (1.21), одержимо систему:

, ,                                                (1.23)

яка завжди розв'язна відносно , тому що (1.21) – загальне розв'язання системи (1.16). Після підстановки знайдених значень  в (1.21) одержимо шукане розв'язання задачі Коші:

, .                                               (1.24)

Іноді у формулі загального розв'язання (1.21) роль довільних постійних  грають початкові значення  шуканих функцій. Тоді формули (1.21) мають вигляд:

, ,                                       (1.25)

і така форма загального розв'язання системи (1.16) називається загальним розв'язанням у формі Коші.

Розв'язання системи (1.16), що складається тільки із точок одиничності розв'язання задачі Коші для цієї системи, називається частинним розв'язанням системи. Очевидно, що розв'язання, отримане по формулах загального розв'язання (1.21) при заданих значеннях довільних постійних  (включаючи й невласні значення ), є приватним розв'язанням системи (1.16).

Розв'язання системи (1.16) у кожній точці якого порушується умова одиничності розв'язання задачі Коші для цієї системи, називається особим розв'язанням системи.

Приклад. Знайти особі розв'язання системи:

,

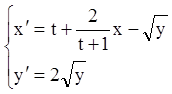де , .

Розв'язання. Праві частини цієї системи неперервні в розглянутій області. Частинні похідні 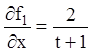; ; 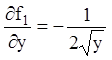 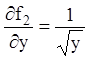є необмеженими при . Тому не виключена можливість існування особих розв'язань цієї системи. Знайдемо їх. Із другого рівняння при  знаходимо 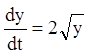; ; 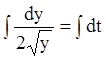 . Тому що , те . Але, мабуть, є розв'язанням другого рівняння, і це його особе розв'язання.

Підставивши знайдене значення  в перше рівняння системи, одержимо:

I.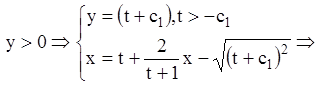

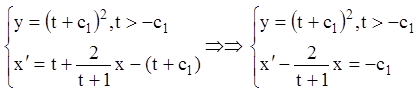;                                 (1.26)