Системи звичайних диференціальних рівнянь. Теорія лінійних систем, страница 5

Припускається, що  – неперервна функція своїх аргументів з неперервними частинними похідними, причому – це істотно – не залежить явно від . Якщо ж ні в області , ні в якійсь її частині залежність (1.38) не має місця, то функції  називають незалежнимив  (жодна з функцій  не виражається через інші). Для незалежності функцій  у  необхідно й досить, щоб функціональний визначник (визначник Остроградського) не звертався в нуль в області , тобто:

.

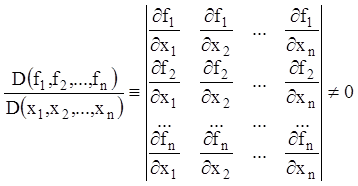Доведення.Припустимо, що ми маємо  незалежних інтегралів системи (1.16): , , ..., , тобто таких, що функціональний визначник:

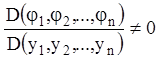.                                                       (1.39)

Ще припустимо, що нам удалося знайти ще один інтеграл  цієї системи. Тоді, з визначення інтеграла системи, маємо тотожності:

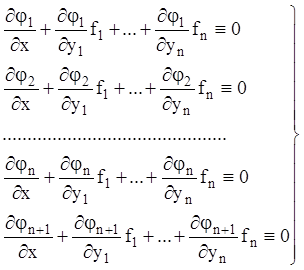.                                         (1.40)

Спільне існування тотожностей (1.40), у які входять не рівні нулю величини , можливо тоді, і тільки тоді, коли визначник цієї системи (визначник Остроградського) тотожно дорівнює нулю, тобто:

.

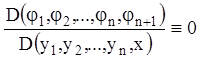Але за умовою теореми 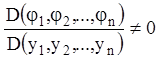, тому що функції  — незалежні між собою відносно . Тоді по теоремі про залежності функцій , тобто -й інтеграл є функцією  незалежних інтегралів і не є новим інтегралом системи, що й було потрібно довести.

Зауваження. З теореми Коші про існування й одиничність розв'язання системи (1.16) треба, що вона завжди має  незалежних інтегралів, Тому, якщо яким-небудь способом удалося знайти  незалежних інтегралів , , ...,  системи (1.16), задача її інтегрування закінчена. Сукупність

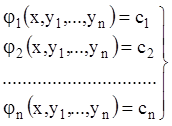                                                     (1.41)

називають загальним інтегралом системи (1.16), а кожна рівність – першим інтегралом. З попередніх міркувань треба, що існує нескінченна множина перших інтегралів системи. Їх ми можемо знаходити, роблячи ті або інші перетворення нормальної системи.

1.5 Симетрична форма системи диференціальних рівнянь

Розглянемо систему диференціальних рівнянь виду:

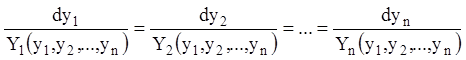.                     (1.42)

Всі змінні, вхідні в (1.42) рівноправні, у той час як у нормальній системі

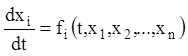
                                        (1.43)

 – незалежна змінна, а  – шукані функції, тобто змінні не рівноправні.

Систему (1.42) називають системою звичайних диференціальних рівнянь у симетричній формі.

Нормальну систему (1.43) завжди можна привести до симетричної форми. Для цього досить її записати у вигляді:

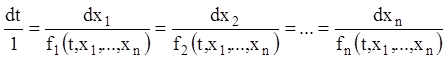.                       (1.44)

Цю систему називають системою диференціальних рівнянь першого порядку в симетричній формі, що відповідає нормальній системі (1.43). Всі змінні , входять в (1.44) уже рівноправно.

Якщо всі функції  системи (1.44) є дробами з тим самим знаменником , то після множення на нього всіх знаменників у системі (1.44), одержимо:

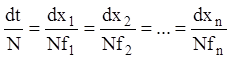.                                             (1.45)

Якщо в цьому випадку ввести позначення для всіх змінних 

, , , ...,                                     (1.46)

і симетричні позначення для всіх знаменників

, , ..., ,

то система (1.45) запишеться:

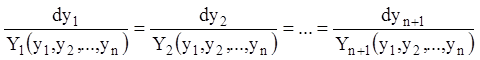.                        (1.47)

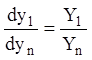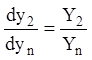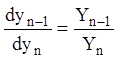; ; ...; .                                (1.48)

Розв'язання, інтеграл, перший інтеграл, загальне розв'язання й загальний інтеграл системи (1.48) називають відповідно рішенням, інтегралом, першим інтегралом, загальним розв'язанням і загальним інтегралом системи (1.42).

1.6 Методи розв'язання систем

1.6.1. Послідовне інтегрування

Якщо кожне рівняння нормальної системи диференціальних рівнянь містить тільки одну невідому функцію, тобто:

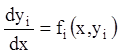
  ,                                             (1.49)

то її інтегрування зводиться до інтегрування кожного з рівнянь окремо.

Якщо нормальна система має вигляд:

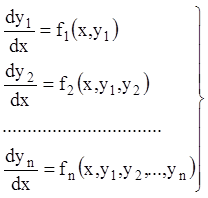,                                                    (1.50)

її інтегрування виконується послідовно: потрібно проінтегрувати перше рівняння й знайдене значення загального розв'язку підставити в друге рівняння, проінтегрувати, і так далі.

Зокрема, таким шляхом може бути проінтегрована у квадратурах лінійна система виду: