Системи звичайних диференціальних рівнянь. Теорія лінійних систем, страница 11

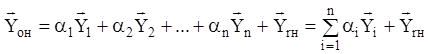
можна так підібрати довільні постійні , щоб виконувалися довільно задані початкові умови:

,

тобто треба довести, що векторне рівняння:

або еквівалентна система рівнянь:

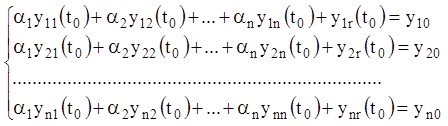                              (1.91)

завжди має розв'язання , які б не були праві частини. Це твердження очевидно, тому що визначник системи (1.91) є визначником Вронського в точці  для фундаментальної системи розв'язань  відповідної однорідної системи й по теоремі 4 відмінний від нуля. Отже, система (1.91) має розв'язання  при будь-яких правих частинах. Значить .

Теорема 10 (принцип суперпозиції). Розв'язанням системи лінійних рівнянь 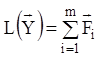, де  є сума  розв'язань  рівнянь  .

Доведення. Дано  . Треба довести, що 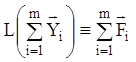. Використовуючи властивість 2 оператори , одержимо .

1.8. Метод варіації довільних постійних, розв'язання лінійних неоднорідних систем (метод Лагранжа)

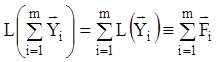Нехай дана лінійна неоднорідна система

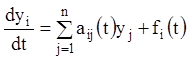
 ,                                       (1.92)

загальне розв'язання якої потрібно знайти, причому відомо, що відповідна однорідна система

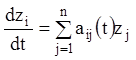
                                               (1.93)

має загальне розв'язання

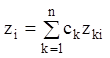
 ,                                                (1.94)

де  – деяка фундаментальна система розв'язань однорідної системи (1.93), а  – довільні постійні. Будемо шукати загальне розв'язання неоднорідної системи (1.92) у вигляді

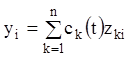
 ,                                            (1.95)

де  – деяка фундаментальна система розв'язань відповідної однорідної системи, а  – деякі безупинно диференційовані функції від .Виберемо ці функції так, щоб (1.95) давала розв'язання системи (1.92). Для цього підставляємо (1.95) в (1.92) і одержуємо:

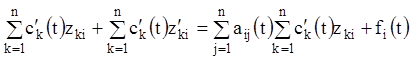
                (1.96)

або

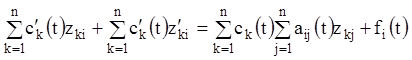
                (1.97)

Переписавши рівності (1.97) у вигляді:

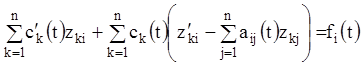
                  (1.98)

і з огляду на те що  – фундаментальна система розв'язань відповідної однорідної системи (1.93), одержуємо наступну систему  рівнянь для визначення  :

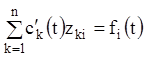
  .                                      (1.99)

Тому що визначник цієї системи, будучи вронськіаном фундаментальної системи розв'язань, відмінний від нуля ( ), то розв'язавши її відносно , знаходимо:

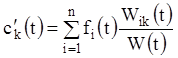
  ,                                   (1.100)

де  є алгебраїчне доповнення елемента  вронськіана . Інтегруючи (1.100), знаходимо :

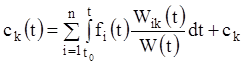
  .                            (1.101)

Підставляючи знайдені значення  у формулу (1.95), одержуємо:

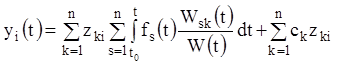
  .                 (1.102)

Розв'язання (1.102) є загальним розв'язанням системи (1.92).

Приклад. Розв’язати систему методом Лагранжа

.

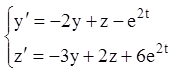Розв'язання. Легко перевірити, що загальним розв'язанням відповідної однорідної системи

,

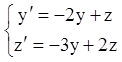буде система функцій:

;

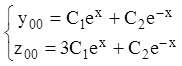Шукаємо частинне розв'язання неоднорідної системи у вигляді

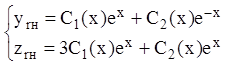                                                (1. 103)

У нашому випадку система (1.95) має вигляд

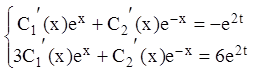
звідки ,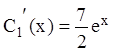

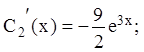
Отже, , .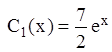

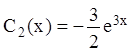Підставляючи ці значення в систему (1.103), одержимо частинне розв'язання даної системи:

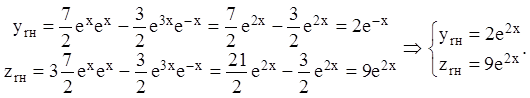
Тоді по теоремі 9 загальне розв'язання неоднорідної системи запишеться:

.

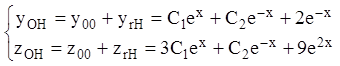Розглянемо варіант методу варіації довільних постійні розв'язання задачі Коші для векторного рівняння:

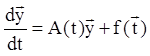; .                                          (1.104)

Припустимо, що нам відома матриця  яка є розв'язанням однорідної задачі

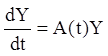;     ,                                           (1.105)

яка називається нормальною інтегральною матрицею. Будемо шукати розв'язання задачі (1.104) у вигляді

                                                     (1. 106)

де  шуканий безупинно диференційований вектор.

Після підстановки (1.106) у рівняння (1.104) одержимо:

звідки, з огляду на тотожність  одержуємо:

Отже,

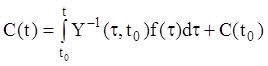.                                            (1.107)

У силу початкових умов (1.104), (1.105) і формули (1.106), знаходимо:

.

Після підстановки (1.107) в (1.106) знаходимо

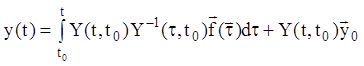.                                (1.108)

Ця формула дає розв'язання задачі (1.104) і називається формулою Коші.