(причому необов'язково, щоб
всі співвідношення брали участь у цій комбінації). При цьому множники ![]() підбирають так, щоб знаменник дорівнював
нулю, а чисельник був повним диференціалом або ж знаменником не дорівнює нулю,
але чисельник був диференціалом тієї комбінації змінних, котрої виражається
знаменник.
підбирають так, щоб знаменник дорівнював
нулю, а чисельник був повним диференціалом або ж знаменником не дорівнює нулю,
але чисельник був диференціалом тієї комбінації змінних, котрої виражається
знаменник.
Приклад.Проінтегрувати систему:
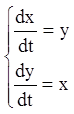 .
.
Розв'язання. Складаючи рівняння й віднімаючи з першого рівняння друге, одержимо відповідно:
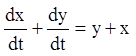
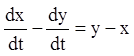
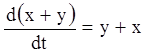
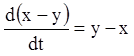
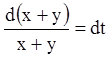
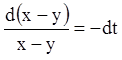
![]()
![]()
![]()
![]()
Тобто одержали розв'язання системи:
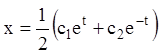 ,
, 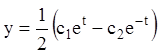 .
.
Приклад.Проінтегрувати систему:
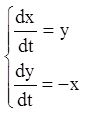 .
.
Розв'язання. Помножимо рівняння заданої системи на ![]() й
й ![]() відповідно.
Тоді
відповідно.
Тоді
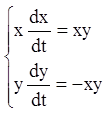 .
.
Складаючи рівняння, одержуємо 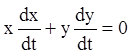 , або
, або ![]() , або
, або 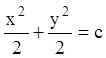 , або
, або ![]() , або
, або ![]() , або
, або ![]() й підставляємо в перше рівняння системи,
одержуємо:
й підставляємо в перше рівняння системи,
одержуємо:
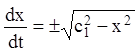 ;
; 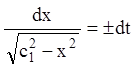 ;
;
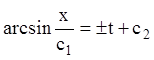 ;
; 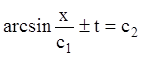 ;
; 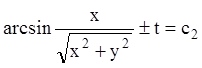 .
.
Перші інтеграли системи:
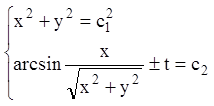 .
.
Приклад. Проінтегрувати систему в симетричній формі:
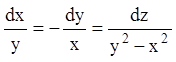 .
.
Розв'язання. Тaк як 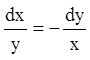 , то
, то ![]() або
або ![]() –
перший інтеграл. Із другого рівняння:
–
перший інтеграл. Із другого рівняння:
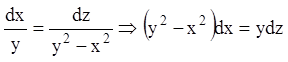 ;
; ![]() .
.
Ділимо на ![]() :
:
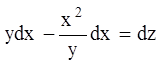 (1.72).
(1.72).
Тому що 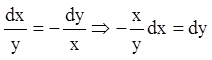 . Тоді (1.72) запишеться:
. Тоді (1.72) запишеться:
![]() .
.
Перші інтеграли системи:
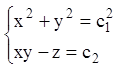 .
.
Приклад. Знайти загальний інтеграл системи:
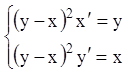 .
.
Розв'язання. Запишемо систему в симетричній формі 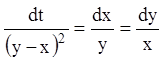
![]()
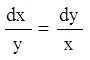
![]()
![]()
![]()
![]() – перший інтеграл. Використовуючи
властивість ряду рівних співвідношень, одержуємо
– перший інтеграл. Використовуючи
властивість ряду рівних співвідношень, одержуємо 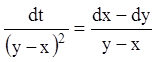 або
або ![]() або
або ![]() або
або 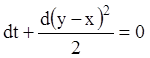 або
або ![]() –
перший інтеграл системи.
–
перший інтеграл системи.
Відповідь: 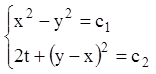 .
.
Приклад. Розв’язати систему:
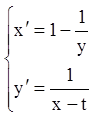 .
.
Розв'язання. Записуємо систему в симетричній формі:
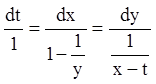 або
або 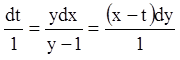 .
.
Використовуючи властивість ряду рівних співвідношень одержуємо:
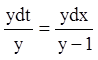
![]()
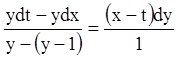
![]()
![]()
![]()
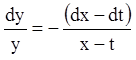
![]()
![]()
![]()
![]() (1.73)
(1.73)
– перший інтеграл.
Звідси 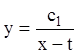 . Підставляючи в перше рівняння
системи, знаходимо:
. Підставляючи в перше рівняння
системи, знаходимо:
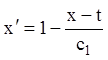
або:
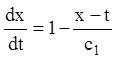
![]()
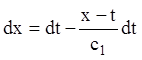
![]()
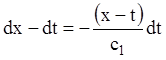
![]()
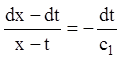
![]()
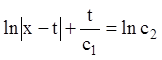
![]()
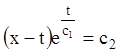
або з огляду на (1.73),
одержуємо 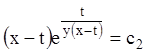 – інтеграл системи.
– інтеграл системи.
Загальний інтеграл:
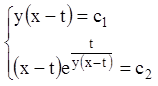 .
.
Приклад.Розв’язати
систему: 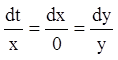 .
.
Розв'язання. З перших двох співвідношень ![]()
![]()
![]()
![]() –
перший інтеграл системи. Із другого рівняння
–
перший інтеграл системи. Із другого рівняння 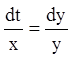 й з
огляду на, що
й з
огляду на, що ![]() , одержуємо
, одержуємо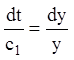
![]()
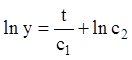
![]()
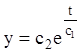
![]()
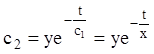 , тобто
, тобто![]() –
перший інтеграл. Загальний інтеграл:
–
перший інтеграл. Загальний інтеграл:
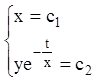 .
.
Як було указане вище, система диференціальних рівнянь називається лінійної, якщо вона лінійна щодо всіх невідомих функцій й їхніх похідних. Система лінійних диференціальних рівнянь (1.5) у скалярній формі має вигляд
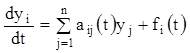
![]() ,
(1.74)
,
(1.74)
де ![]() й
й
![]() – задані неперервні функції в інтервалі
– задані неперервні функції в інтервалі ![]() . Якщо увести матрицю
. Якщо увести матрицю ![]() порядку
порядку ![]() й
й ![]() - мірні вектори
- мірні вектори ![]() й
й
![]() , а саме:
, а саме:
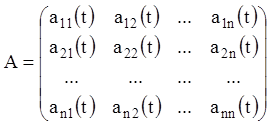 ,
,
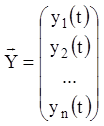 ,
, 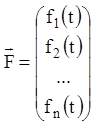 ,
, 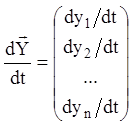 ,
,
то система (1.74) запишеться у векторній формі
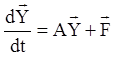 .
(1.75)
.
(1.75)
Відповідно до дій над матрицями й рівності матриць маємо
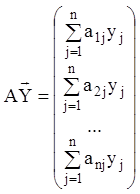 ,
, 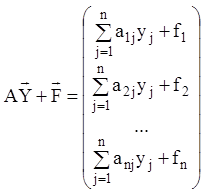 ,
, 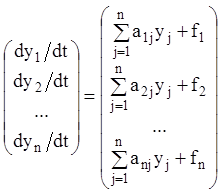 ,
,
звідки витікає, що векторне
рівняння (1.75) еквівалентно системі (1.74). Система (1.75) є неоднорідною
лінійною системою. Якщо всі ![]()
![]() ,
система є однорідною лінійною системою. Однорідна система у векторній
формі має вигляд
,
система є однорідною лінійною системою. Однорідна система у векторній
формі має вигляд
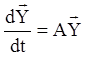 . (1.76)
. (1.76)
Задача Коші для векторного рівняння (1.75) ставиться так: знайти розв'язання рівняння (1.75), якщо
![]() ,
(1.77)
,
(1.77)
де ![]() –
будь-яка точка інтервалу
–
будь-яка точка інтервалу ![]() , а
, а ![]() – будь-який заданий
– будь-який заданий ![]() - мірний вектор
- мірний вектор ![]() .
Розв'язанням задачі (1.75) - (1.77) називається такий диференційований вектор
.
Розв'язанням задачі (1.75) - (1.77) називається такий диференційований вектор
![]() ,
,
який задовольняє на ![]() рівнянню (1.75) і початковій умові (1.77).
рівнянню (1.75) і початковій умові (1.77).
Якщо всі функції ![]() й
й ![]() в (1.75) неперервні на інтервалі
в (1.75) неперервні на інтервалі ![]() , то в досить малій околиці кожної точки
, то в досить малій околиці кожної точки ![]() , де
, де ![]() ,
виконані умови теореми існування й одиничності розв'язання задачі Коші й, отже,
через кожну таку точку проходить єдина інтегральна крива системи (1.75).
Дійсно, у цьому випадку праві частини системи (1.75) неперервні, і їхні
частинні похідні по кожному
,
виконані умови теореми існування й одиничності розв'язання задачі Коші й, отже,
через кожну таку точку проходить єдина інтегральна крива системи (1.75).
Дійсно, у цьому випадку праві частини системи (1.75) неперервні, і їхні
частинні похідні по кожному ![]() обмежені, тому що ці
частинні похідні рівні неперервними на інтервалі
обмежені, тому що ці
частинні похідні рівні неперервними на інтервалі ![]() коефіцієнтам
коефіцієнтам
![]() .
.
Введемо в розгляд лінійний оператор ![]() рівністю
рівністю
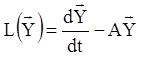 , тоді неоднорідне рівняння (1.75) запишеться
у вигляді:
, тоді неоднорідне рівняння (1.75) запишеться
у вигляді:
![]() ,
(1.78)
,
(1.78)
а однорідне (1.76) у вигляді:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.