Системи звичайних диференціальних рівнянь. Теорія лінійних систем, страница 9

.                                                           (1.79)

Цей оператор має дві основні властивості:

1) , де  – довільна постійна.

2) , де  й  — вектори.

Доведення.Дійсно,

,

.

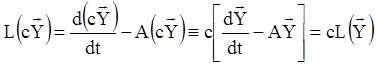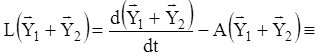
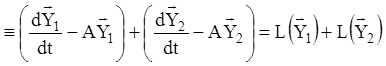Наслідком властивостей 1 й 2 є 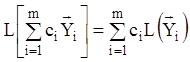, де  – довільна постійна.

Теорема 1. Якщо  є розв'язанням лінійної однорідної системи , то , де  – довільна постійна, теж буде розв'язанням тієї ж системи.

Доведення.Дано , доведемо що . Використаємо властивість 1 оператора :   , що й було потрібно довести.

Теорема 2. Якщо  і  є розв'язаннями однорідної лінійної системи , то сума  теж є розв'язанням тієї ж системи.

Доведення.Дано , . Потрібно довести, що .Використовуючи властивість 2 оператори , одержуємо , що й було потрібно довести.

Наслідок теорем 1 й 2. Якщо , розв'язання однорідної лінійної системи , то лінійна комбінація 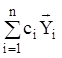, де  – довільні постійні, теж є розв'язанням тієї ж системи.

Теорема 3. Якщо лінійна однорідна система  з дійсними коефіцієнтами  має комплексне розв'язання , то дійсна й мнима частини окремо і  є розв'язаннями тієї ж системи.

Доведення.Дано . Треба довести, що  й . Користуючись властивостями 1 й 2 оператори , одержуємо . Отже,  і , що й було потрібно довести.

Система векторів (розв'язань рівняння (1.71)) , де  називається лінійно залежною на відрізку , якщо існують такі не рівні нулю одночасно постійні , що:

, при .                                 (1.80)

Якщо ж тотожність (1.80) справедлива лише при , то вектори  називаються лінійно незалежними на .

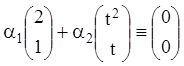Наприклад, два вектори  й  очевидно є лінійно незалежними на довільному інтервалі , тому що тотожність  виконується лише при .

  .

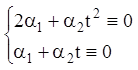
Відзначимо, що одна векторна тотожність (1.80) еквівалентно  тотожностям:

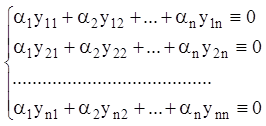                                             (1.81)

Якщо вектори   лінійно залежні, то це значить, що існує нетривіальна система , що задовольняє системі (1.81) лінійних однорідних по відношенню  рівнянь, а її визначник

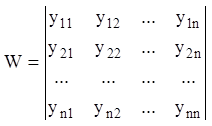
повинен дорівнювати нулю для всіх значень . Цей визначник системи називають визначником Вронського для системи векторів .

Теорема 4.Якщо визначник Вронського  розв'язань  лінійної однорідної системи  з неперервними на  коефіцієнтами  дорівнює нулю хоча б в одній точці , то розв'язання  лінійно залежні на  й на розглянутому відрізку .

Доведення Тому що визначник Вронського системи розв'язань  , отже існує набір , для якого:

.                                      (1.82)

Покладемо

,                                       (1.83)

де   ті ж самі, що й у рівності (1.82). Вектор-функція (1.83) задовольняє рівнянню  й, крім того, у силу (1.82) – початковій умові .

На підставі теореми існування й одиничності ( неперервні) укладаємо, що вектор-функція

.                                  (1.84)

Тому що не всі   дорівнюють нулю, то з (1.84) треба лінійна залежність векторів   на , а звідси треба, що , .

Означення.Систему  лінійно незалежних розв'язань  лінійної однорідної системи  називають фундаментальною системою розв'язань (скорочено ф.с. р.) або базисом однорідної системи.

Тотожним поняттям поняттю ф.с. р. є поняття інтегральної матриці системи

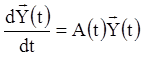.                                                 (1.76)

Інтегральною матрицею системи (1.76) називають квадратичну матрицю , стовпцями якої є  лінійно незалежних розв'язань системи. Тому що кожен стовпець матриці  задовольняє рівнянню (1.76), те й інтегральна матриця  задовольняє рівнянню

.

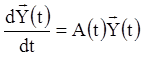Теорема 5.Якщо коефіцієнти  ЛОС неперервні в інтервалі , то існує фундаментальна система розв'язань, визначених і неперервних у цьому інтервалі (тобто існує інтегральна матриця системи).

З теореми про існування й одиничність розв'язання системи ЛДР треба, що інтегральна матриця  однозначно визначається, якщо задано значення цієї матриці при якомусь («початковому ») значенні , . Як матриця  можна взяти будь-яку невироджену квадратну матрицю -го порядку. В окремому випадку, якщо , інтегральну матрицю  називають нормованою.