Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 7

6.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції).

6.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 408-420.

6.6. На практичному занятті використовуються формули, таблиці, теореми.

          1). Комплексна форма запису ряду Фур’є.

Використаємо формули Єйлера:

      .

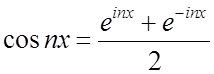
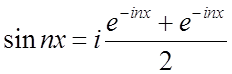Введемо  позначення:

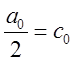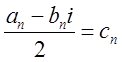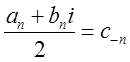 ,  ,  .                                                (6.1)

Тоді     =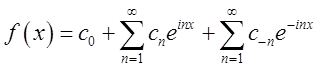

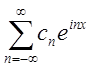
Таким чином, ми одержали розвинення функції  у функціональний ряд з комплексними членами. Він називається  рядом Фур'є в комплексній формі.                                                (6.4)

2). Представлення функції інтегралом Фур’є.

Представлення функції  в сегменті  рядом Фур'є (5.2)

                                                      

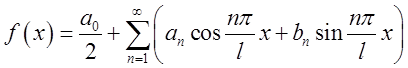
можна витлумачити в такий спосіб. Якщо функція  в сегменті є «досить гарної» (саме, якщо вона в цьому проміжку задовольняє умовам Дирихле), то для того, щоб її в цьому сегменті цілком описати, досить указати деякий, цілком визначений набір її характеристик, коефіцієнтів Фур'є (див. (5.3)):

,      ,     

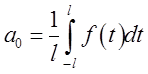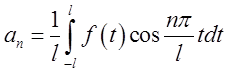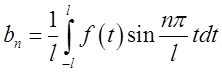
Таким чином, коефіцієнти Фур'є несуть у собі досить інформації про поводження функції у відповідному кінечному сегменті, як би великий він ні був.

3). Комплексна форма інтегралу Фур’є:

Повернемося до інтегральної формули Фур'є

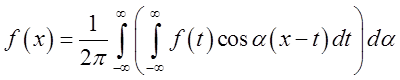                                                     (6.5)

і застосуємо до наявного в цій формулі косинусу формулу Эйлера:

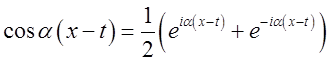 . Ми одержимо

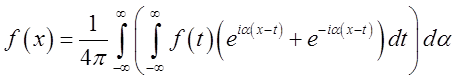 , чи  .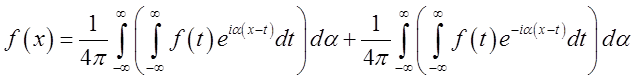

Тут, як неважко переконатися підстановкою  , інтеграли, що стоять у правій частині, рівні один одному. Тому

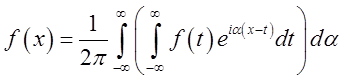                                                             (6.7)

Отримана формула називається розкладанням функції в інтеграл Фур'є в комплексній формі.

          4). Поняття про перетворення Фур’є.

Перепишемо формулу (6.7), заміняючи a на , у наступному виді:

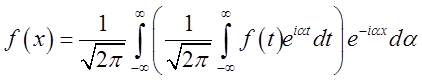 , і покладемо 

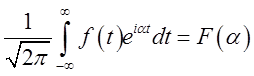                                                                          (6.8)

Тоді, очвидно, буде 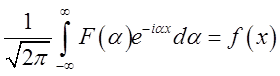                                    (6.9)

Визначення. Перехід від функції   до функції  , описуваний формулою (6.8), називається перетворенням Фур'є функції . Часто перетворенням Фур'є функції  називається сама функція . Зворотний перехід від функції  до функції , описується формулою (6.9), називається зворотним перетворенням Фур'є. Також зворотним перетворенням Фур'є функції  називається функція .

6.7. Вправи на засвоєння матеріалу.

1).  Розв’яжемо декілька прикладів:

 ПРИКЛАД 1.

 Знайдемо інтеграл Фур'є в комплексній формі для функції

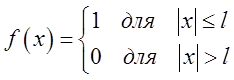
Розв’язок:

У цьому випадку обчислення внутрішнього інтеграла в правій частині формули (6.7) дає нам

 .

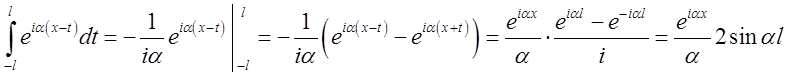Тому формула (6.7) набуває в даному випадку такого виду:   .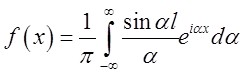

Відповідь: .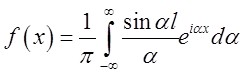

ПРИКЛАД 2.

Розвинемо в інтеграл Фур'є в комплексній формі функцію 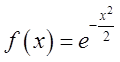     Ми маємо

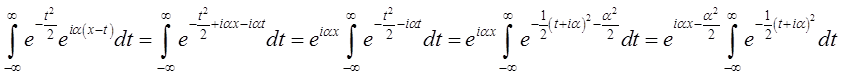 Останній інтеграл є функцією від a. Позначимо його через  і обчислимо його. Ми маємо       

 ,

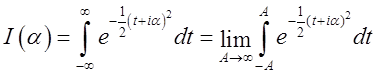 роблячи підстановку , ми одержимо .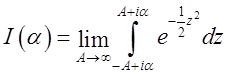

Продиференцюємо ця тотожність по a. Через те, що збіжність до границі по a є рівномірною в  будь-якому кінцевому проміжку, диференціювання під знаком границі законно. Ми маємо 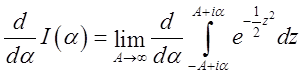. Виконуючи диференціювання інтеграла по верхній і нижній границях, ми одержуємо

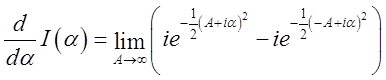 , а згадуючи формулу (6.5) і переходячи до границі, будемо мати 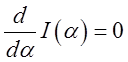. Отже, первісна функція повинна бути постійної:   . Зокрема, повинне бути . Обчислимо інтеграл . Запишемо його для цього двічі:

 , і перемножимо почленно ці рівності. Ми одержимо    .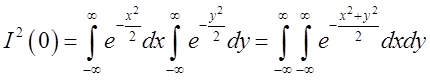

Переходячи в подвійному інтегралі до полярних координат, ми маємо

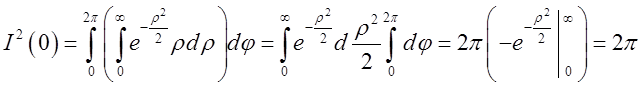 , відкіля . Таким чином,

                                                                            

і шуканим розвиненням в інтеграл Фур'є є         .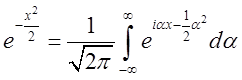

Практичне заняття 7.

План:

7.1.Тема. Дослідження подвійних інтегралів, їх властивостей. Обчислення в декартових координатах. Заміна змінних у подвійних інтегралах.