Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 19

Розв’язок:

Згідно формули (*) маємо:    .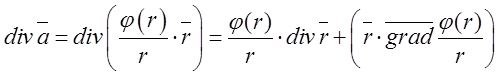

З попереднього  прикладу 1   а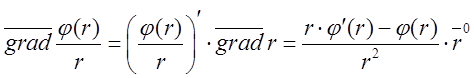 

А тому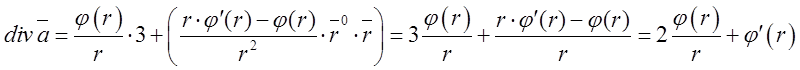

Відповідь: .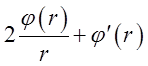

ПРИКЛАД 5

Обчислити циркуляцію поля  вздовж еліпса .

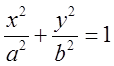Розв’язок:

Скористаємось формулою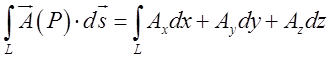                                                                                 

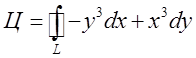 . Зводячи цей інтеграл до звичайного, рівняння контура запишемо в параметричному виді 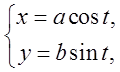 при .

Підставимо 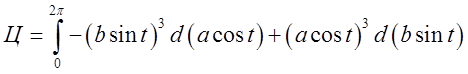 = =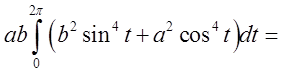 = =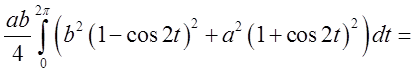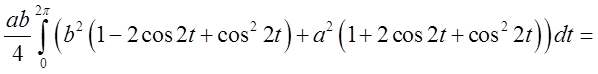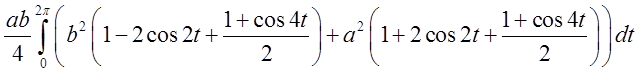.  Очевидно, що 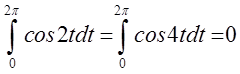, а тому 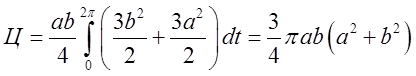. Це і є відповідь.

ПРИКЛАД 6.

 Обчислимо циркуляцію вектора поля лінійних швидкостей тіла, яке  обертається з швидкістю  вздовж контура L , розташованого повністю в площині П.

Розв’язок:

 З вигляду векторного поля бачимо, що  – кутова швидкість, Оz – вісь обертання (рис.12.1)

Рис.12.1.                 

 Нормаль  до площини П утворює з осями координат кути . Напрямок обходу контуру L і напрямок нормалі  погоджені між собою так, як у теоремі Стокса.Відповідно до визначення циркуляція дорівнює

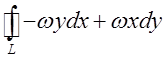. Застосуємо для обчислення цього інтегралу теорему Стокса: 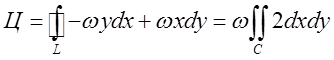, де С – область, обмежена контуром L. Інтегрування ведеться по верхній строні площини П і тому . У нас . Так як С частина площини П то циркуляция дорівнює 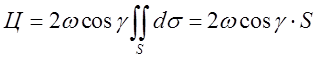, де S – площа області С, обмеженої контуром L. Зауважимо, що  – проекція вектора  на напрямок вектора . Тому остаточно вираз для циркуляції прийме вигляд

ПРИКЛАД 7.

 Обчислити ротор векторного поля:  

Розв’язок:

 Використаємо формулу  .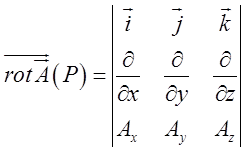                                                              

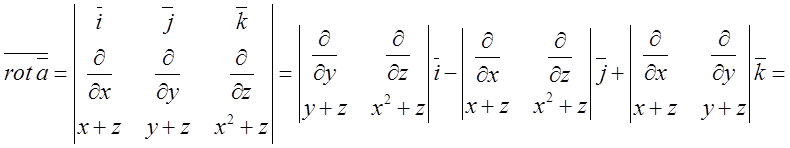
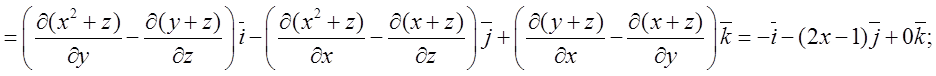
Відповідь: .

ПРИКЛАД 8.

Знайти ротор вектора напруженості магнітного поля нескінченно довгого провідника по якому тече струм силою І.

Розв’язок

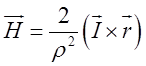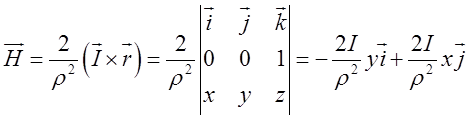
 Введемо систему координат, спрямувавши вісь провідника вздовж вісі Оz. Як відомо з фізики, вектор напруженості магнітного поля, створеного струмом, дорівнює . Завдяки обраній системі координат ми можемо, знаючи величину струму І, знайти . Так як напрямним одиничним вектором для напрямку провідника є орт  (вісь провідника співпадає з віссю Оz), то .   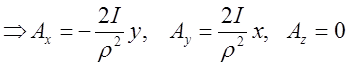 , де . Знаходимо ротор вектора напруженості, застосовуючи (12.5).

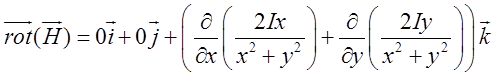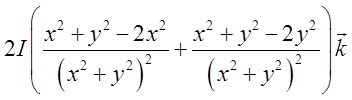==0.

Звідси бачимо, що=0 всюди крім вісі Оz, де він не визначений (при х=у=0 знаменник обертається в нуль). А це значить, що магнітне поле вектора  всюди є безвихрове крім точок , які знаходяться на вісі провідника струму.

ПРИКЛАД 9.

Знайти поток вектора r(M) через замкнуту поверхню, задану рівняннями  (мал. 2)

Розв’язок:

В цьому виподку замкнута поверхня складається з бокової поверхні і двох основаній циліндра.

Поток запишеться у вигляді слідуючій суми:

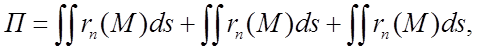
де -проекція радіуса вектора r(M) на зовнышню нормаль до поверхны.

На боковій поверхні циліндра зовнішня нормаль паралельна плоскості xoy і проєкція  дорівнює а.

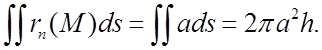
На нижній основі радіус-вектор r(M) перпендикулярний зовнішній нормалі. Тому маємо:

На верхній основі зовнішня нормаль направляє позитивному напрямку до вісі oz, тому

З цього слідує,

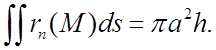
получаємо:

Відповідь:

2) Розв’язати самостійно:

14.1. Знайти дивергенцію векторного поля , де  – постійний вектор.

          Відп. 0.

14.2. Знайти дивергенцію векторного поля , де  – постійний

         вектор.    Відп. 0.

14.3. При якій функції  дивергенція поля  буде дорівнювати z?

                   Відп. .

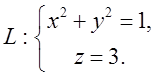14.4. Обчислити циркуляцію Ц вектора  вздовж  лінії    Відп. .

14.5. Обчислити циркуляцію Ц вектора вздовж  лінії 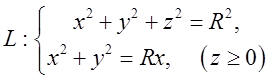. Відп..

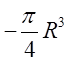14.6. Знайти ротор слідуючих векторних полів:

         а) .  Відп..

        б)    . Відп..

         в) 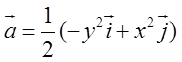  . Відп..

14.7. Яка повинна бути функція , щоб ?

         Відп..

14.8. Застосовуючи теорему Стокса, обчислити циркуляцію вектора  по контуру 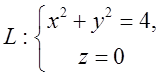. Відп..

14.9. Застосовуючи теорему Стокса, обчислити циркуляцію вектора  по контуру 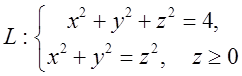. Відп.–.

14.10. Застосовуючи теорему Стокса, обчислити циркуляцію вектора  по контуру утвореному перетином площини  з координатними площинами. Відп.4/3.