Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 18

9. Обчислити потік векторного поля  через повну поверхню піраміди, обмеженої площинами . Відп.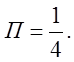

10. Обчислити потік векторного поля  через сферу . Відп.

Практичне заняття 14.

План:

14.1Тема. Дослідження теорії поля. Дивергенція векторного поля.  Циркуляція і ротор векторного поля. Оператори Гамільтона і Лапласа.

14.2Ціль:

1). Засвоїти дивергенцію векторного поля.

2). Засвоїти ціркуляцію і ротор векторного поля.

3). Засвоїти оператори Гамільтона і Лапласа.

14.3. Теоретичний матеріал подано в лекції номер 1.

14.4. Опитування студентів з теоретичного курсу (запитання подані в кінці лекції) .

14.5. Додаткову літературу можна використати таку:Бермант А. Ф., Араманович И. Г. Краткий курс математического аналмза (издание любое стереотипное) стор. 511-522.

14.6. На практичному занятті використовуються формули, таблиці, теореми, означення.

          1)Дивергенція векторного поля.

Означення. Дивергенцією або розбіжністю векторного поля  у точці Р називається границя відношення потоку вектора через поверхню, що оточує точку Р до  об’єму, обмеженому цією поверхнею, за умови, що уся поверхня стягується в точку Р.

Дивергенцію поля позначають символом . Таким чином

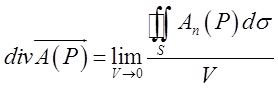
векторного поля є величина скалярна.

Теорема. Дивергенція  векторного поля виражається формулою        ,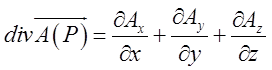                      

де значення частинних похідних беруться в точці Р.

Потік вектора зсередини замкнутої поверхні дорівнює потрійному інтегралу по об’єму, обмеженому цією поверхнею, від  дивергенції  поля.

                                                                    

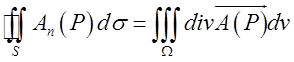
2) Циркуляція і ротор векторного поля.

Означення. Циркуляцією вектора  уздовж замкнутого контуру L називається криволінійний інтеграл по цьому контурі від скалярного добутку вектора  на вектор дотичної до контуру L. Позначатимемо циркуляцію через  Ц.

.

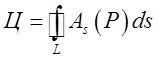Означення. Ротором векторного поля      називається вектор             

 
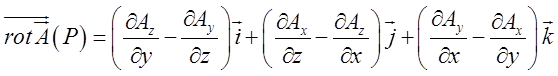
За допомогою визначення ротора теорему Стокса можна подати у векторній формі:

                                                  

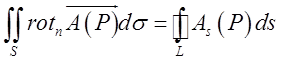
Потік ротора поля через поверхню S дорівнює циркуляції вектора по границі цієї поверхні.

Наведемо дві властивості ротора поля.

1. Перша властивість виражає лінійність ротора і її доведення очевидне.

                               

2. Доведемо ще, що якщо – скалярна функція, а – векторна, то

          3). Оператори Гамільтона і Лапласа.

Розглянемо правила застосування  вектора, який часто називають оператором Гамільтона:

1. Простий добуток цього оператора на скалярну функцію  дає градієнт цієї функції

.                

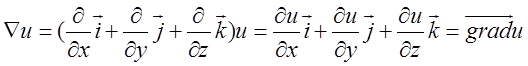2. Скалярний добуток набла-вектора  на векторну функцію  дає дивергенцію цієї функції:

    

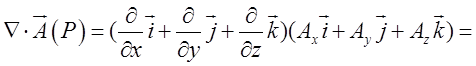
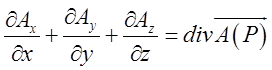
 3. Векторний добуток   набла-вектора  на векторну функцію    дає ротор цієї функції:

              

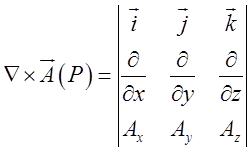
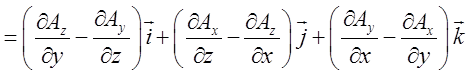
14.7. Вправи на засвоєння матеріалу.

1).  Розв’яжемо декілька прикладів:

 ПРИКЛАД 1.

 Обчислити , де  – радіус вектор точки .

Розв’язок:

Очевидно, що  і тому за формулою маємо: 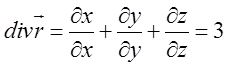. Звідси випливає, що кожна точка заданого  поля є як би джерелом постійної потужності. Користуючись  векторною формою теореми Остроградского, відразу одержуємо, що потік радіуса-вектора через будь-яку замкнуту поверхню дорівнює потроєному об’єму, обмеженому цією поверхнею: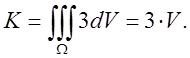

ПРИКЛАД 2.

Обчислити 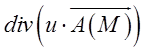, де  – скалярна функція, а  – векторна функція (векторне поле).

Розв’язок:

 Використовуючи 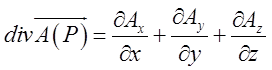,   матимемо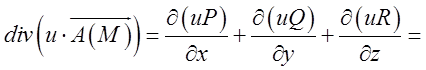 

=

.

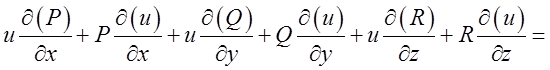
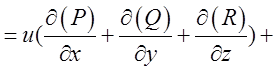
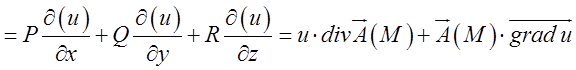Це і є відповідь.

ПРИКЛАД 3.

Обчислимо дивергенцію поля лінійних швидкостей  тіла, що обертається.

Розв’язок:

 Поле швидкостей цього тіла буде плоске. Ми його обчислили в попередній лекції . Як бачимо, , а тому.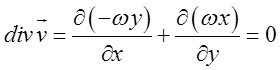

Якщо уявити  рідину, що обертається, як тверде тіло, то ясно, що в такому потоці немає ні джерел, ні стоків.

ПРИКЛАД 4.

Знайти дивергенцію векторного поля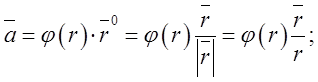 

де  - віддаль від точки  до початку координат,   - радіус вектор цієї точки,   – одиничний вектор напрямку вектора .