Методичні вказівки до практичних та лабораторних занять з дисципліни "Вища математика", страница 10

 Зобразимо  область на рисунку , перетворивши рівняння площини  у рівняння у відрізках: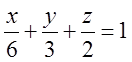. Рівняння прямої АВ на площині  хOу має вид 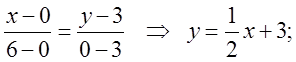  Зовнішній інтеграл беремо вздовж осі ОХ. Очевидно, що 0; середній інтеграл беремо за змінною у. Щоб визначити межі  в яких змінюється у при 0, беремо на відрізку   довільну точку N і проводимо через неї пряму паралельну  осі у. Довжина відрізка NM і буде довжиною по якій ми інтегруємо за  у-ком. Нижній кінець (точна N) цього відрізка на площині має координати ; а верхній – (точка М) . 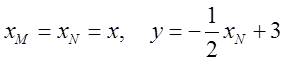Таким чином межі середнього інтеграла будуть 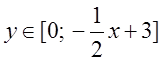.  Щоб визначити межі інтегрування за змінною z, на відрізку NM візьмемо довільну точку Q. Проведемо через неї пряму паралельну осі z. Ця пряма перетне нашу область V в двох точках Q i K. В точці Q вона ввійде в область, а в точці K вийде з неї. Відрізок QK і буде відрізком  інтегрування за змінною z. Очевидно в просторі координати точки Q будуть: 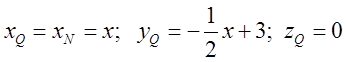. Координати точки K на площині будуть: 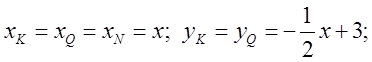 просторову координату z треба знаходити з умови, що точка К лежить на площині 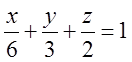 і, якщо дві координати х і у уже визначені, то з рівняння площини 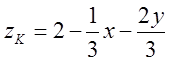 . Таким чином .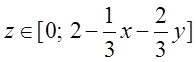

Розставляючи границі інтегрування мислимо слідуючим образом.  Якщо х буде змінюватись від 0 до 6 , а точка Q , буде “бігати” вздовж відрізка MN від N до M, то тоді Q побуває в кожній точці  області обмеженої трикутником  АОВ, а точна К побуває в кожній точці    області, обмеженої трикутником АВС, а тому: .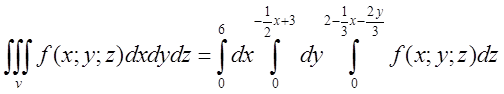

ПРИКЛАД 3.

 Обчислити 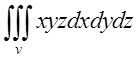 , де V область обмежена поверхнями

Розв’язок:

Область V є трикутна піраміда з основою АВО, у якої бічна грань АОС вигнута поверхня z=xy. Обчислюючи цей інтеграл, всю фігуру зображувати не обов’язково. Границі інтегрування по z задані в умові в явному виді . Границі інтегрування по у теж задані в умові . Лише для змінної х маємо одне значення, а тому побудуємо на площині хОу область  інтегрування. Нею є трикутник ОАВ, рівняння сторін якого будуть: ОА:  у=0;  ОВ:  у=х;  АВ: х=2. Звідси добре видно, що .

.

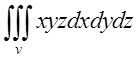
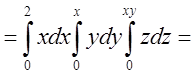
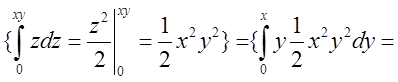
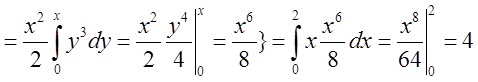Відповідь: 4.

ПРИКЛАД 4.

Обчислити об’єм тіла заданого нерівностями : ;   ;

.

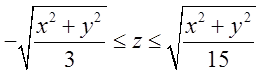Розв’язок:

Розв’язання. Спочатку з’ясуємо якими поверхнями обмежене задане тіло . Для цього зведемо рівняння поверхонь до канонічної форми , перейшовши від нерівностей до рівностей.   це сфера з центром  в.т О(0;0;0) і радіусом 8,  а  - це весь трьохвимірний простір за вийнятком внутрішніх точок (точок, які лежать в середині сфери) .

Анолггічно  це сфера з центром  в.т О(0;0;0) і радіусом 14,  а  - це множина точок, які лежать в середині сфери і на ній..Таким чином нерівність задає сферічне тіло радіусом 14  з вирізаною всередині  його сферою радіусом 8.

Нерівні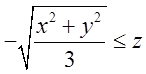сть перетворимо в рівність 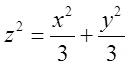 і побачимо, що це конус, а тому

нерівність 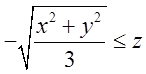 задає множину точок, яка лежить више   конуса  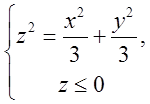           Анологічно  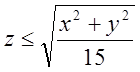 , множина точок , які лежать зовні нижче конуса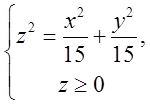   – площина,  –  площина . Нерівність – множина точок, які лежать між цими двома площинами .

Наявність виразів х²+у²+z² спорукає нас на перехід до  сферичної системи координат:

. Переведемо рівняння границь в нову систему координат. 1.  . Це і є границі інтегрування по.

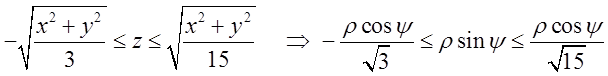
2.  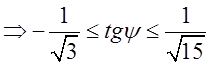  . Звідси легко знайти границі інтегрування по :.

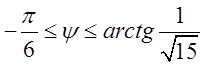
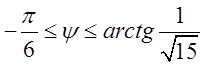 3.   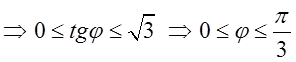      . Це і будуть границі інтегрування по .

=

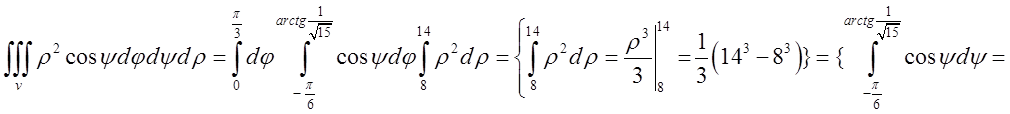
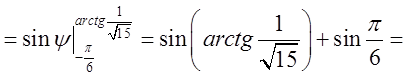
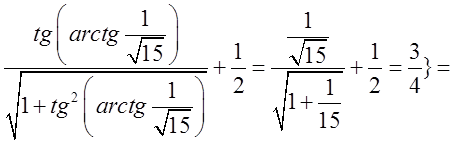
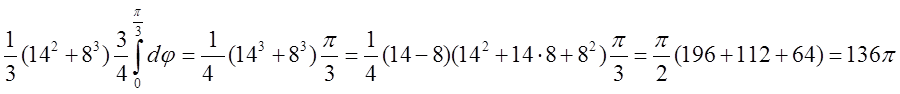
Відповідь. V= куб. одиниць.

2) Розв’язвти самомтійно:                

1.  Обчислити потрійні інтеграли в заданих областях V.

1.1.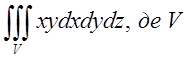– область, обмежена гіперболічним параболоїдом   і площинами

                      Відп.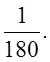

1.2.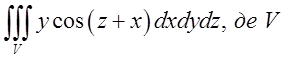– область, обмежена циліндром   і площинами  

                     Відп.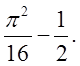

1.3.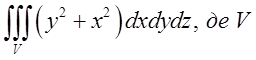– область задана нерівностями .

         Відп. .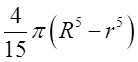

1.4.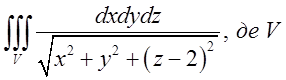– куля .  Відп. .

Практичне заняття 9.

План:

9.1.Тема. Дослідження кратних інтегралів, їх властивостей. Обчислення кратних інтегралів.

9.2.Ціль:

1). Засвоїти кратні інтеграли.

2). Рішення задач за допомогою кератних інтегралів.