Пусть ![]() в окрестности
в окрестности ![]() точки
точки ![]() имеет непрерывную производную
имеет непрерывную производную ![]() - порядка и пусть
- порядка и пусть ![]() .
Тогда по формуле Ньютона – Лейбница
.
Тогда по формуле Ньютона – Лейбница
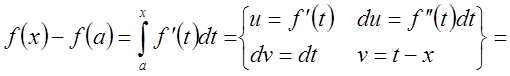

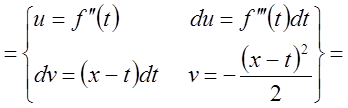
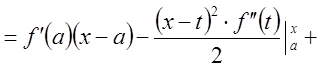
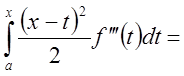
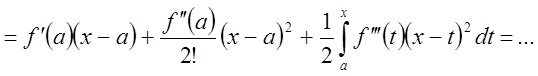
Отсюда
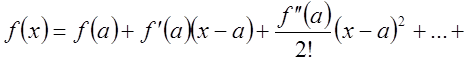
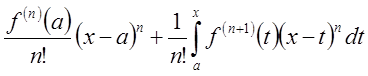 .
.
Итак,
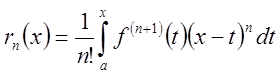 .
.
Замечание.
Если к ![]() в интегральной форме применить
теорему о среднем, то получим
в интегральной форме применить
теорему о среднем, то получим
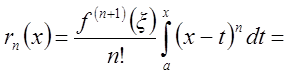
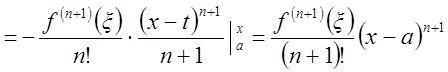
остаточный член в форме Лагранжа.
Лемма:
Пусть ![]() непрерывна
на
непрерывна
на ![]() , а
, а![]() –
возрастающая, неотрицательная, непрерывно дифференцируемая на
–
возрастающая, неотрицательная, непрерывно дифференцируемая на ![]() функция. Тогда существует точка
функция. Тогда существует точка ![]() , такая, что
, такая, что
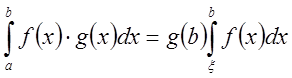 .
.
Доказательство:
Рассмотрим
функцию 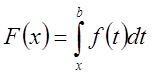 . Очевидно,
. Очевидно,![]() ,
, ![]() ,
, ![]() непрерывна
на
непрерывна
на ![]() и, следовательно, принимает на нем свои
наибольшее и наименьшее значения.
и, следовательно, принимает на нем свои
наибольшее и наименьшее значения.
Если
![]() ,
, ![]() ,
,
то
![]() ,
, ![]() .
.
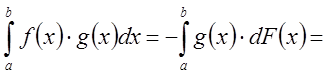
 .
.
По
условию ![]() ; так как
; так как ![]() возрастающая,
то
возрастающая,
то ![]()
![]() .
.
Тогда

![]()
и
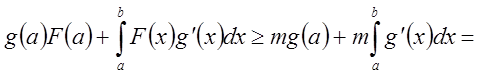
![]() ,
,
следовательно, 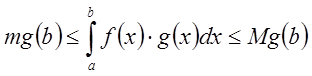 .
.
Если![]() , то так как
, то так как ![]() и
и ![]()
![]() на
на ![]() . Тогда доказываемая формула справедлива
. Тогда доказываемая формула справедлива ![]() .
.
Если
же![]() , то
, то 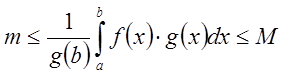 . Значения
непрерывной на
. Значения
непрерывной на ![]() функции
функции ![]() сплошь
заполняют отрезок
сплошь
заполняют отрезок ![]() . Поэтому
. Поэтому ![]() , что
, что 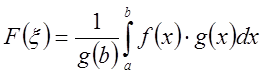 или
или
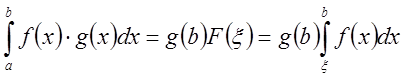 .
.
Теорема:
Пусть ![]() –
непрерывная на
–
непрерывная на ![]() функция, а
функция, а![]() – монотонная, непрерывно дифференцируемая
на
– монотонная, непрерывно дифференцируемая
на ![]() функция. Тогда существует точка
функция. Тогда существует точка ![]() , такая, что
, такая, что
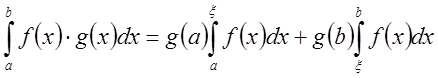 .
.
Доказательство:
Предположим
для определенности, что ![]() возрастает. Рассмотрим
разность
возрастает. Рассмотрим
разность![]() , причем
, причем ![]() .
Применим к
.
Применим к ![]() лемму. Это значит, что
лемму. Это значит, что ![]() такое, что
такое, что 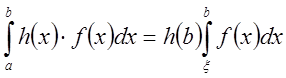 или,
подставляя вместо
или,
подставляя вместо ![]() равное ему выражение, получим
равное ему выражение, получим
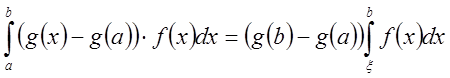 ;
;
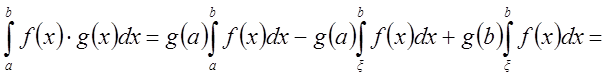
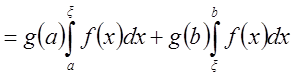 .
.
Пусть задана ![]() .
.
Определение: Кривой
называется множество точек пространства вида ![]() , где
, где ![]() - параметр (можно рассматривать как
время),
- параметр (можно рассматривать как
время), ![]() - параметрические функции, которые
предполагаются непрерывными,
- параметрические функции, которые
предполагаются непрерывными, ![]() - называют параметризацией кривой.
- называют параметризацией кривой.
Точки
кривой соответствующие граничным значениям параметра, т.е. ![]() и
и ![]() -
называют граничными точками кривой.
-
называют граничными точками кривой.
Определение: Простой
кривой называется кривая, задаваемая ![]()
![]() так,
что
так,
что ![]() , (т.е. различным значениям параметра
соответствуют различные точки кривой).
, (т.е. различным значениям параметра
соответствуют различные точки кривой).
Определение: Пусть ![]() и
и ![]() простые
кривые, граничные точки которых совпадают, а остальные нет, тогда кривая
простые
кривые, граничные точки которых совпадают, а остальные нет, тогда кривая ![]() называется простой замкнутой кривой.
называется простой замкнутой кривой.
Одна и та же кривая может быть параметризована различными способами.
Пусть даны две параметризации кривой:
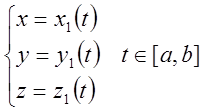
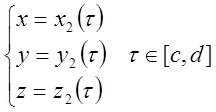 .
.
Будем
говорить, что параметризации эквивалентны, если существует непрерывное, строго
монотонное отображение ![]() отрезка
отрезка ![]() на
на ![]() такое,
что
такое,
что ![]() справедливо равенство:
справедливо равенство:
 .
.
Пример
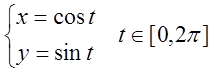 ;
; 
![]() .
.
Пусть
задана кривая ![]() и
и
![]() произвольное разбиение отрезка
произвольное разбиение отрезка ![]() .
.
Пусть
точки ![]() кривой
кривой ![]() соответствующие
разбиению
соответствующие
разбиению ![]() .
.
![]() .
.

Положим , 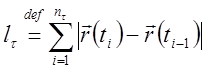 .
.
Очевидно,
![]() и
и ![]() -
длина ломаной
-
длина ломаной ![]() , вписанной в кривую
, вписанной в кривую ![]() .
.
Определение: Кривая ![]() называется спрямляемой, если существует
конечная точная верхняя грань сумм
называется спрямляемой, если существует
конечная точная верхняя грань сумм ![]() , взятая по
всевозможным разбиениям
, взятая по
всевозможным разбиениям ![]() отрезка
отрезка ![]() . Эта точная верхняя грань называется длиной
кривой
. Эта точная верхняя грань называется длиной
кривой ![]() и обозначается
и обозначается ![]() .
Итак,
.
Итак, ![]() .
.
Теорема:
Пусть
дана кривая![]() .
Если функция
.
Если функция ![]() непрерывно дифференцируема на
непрерывно дифференцируема на![]() , то
кривая
, то
кривая ![]() спрямляема
и ее длина вычисляется по формуле:
спрямляема
и ее длина вычисляется по формуле:
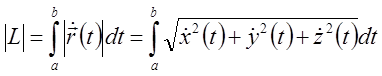 .
.
Доказательство:
Пусть
![]() -
произвольное разбиение отрезка
-
произвольное разбиение отрезка ![]() .
.
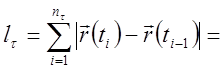 {по формуле Ньютона -
Лейбница}=
{по формуле Ньютона -
Лейбница}=
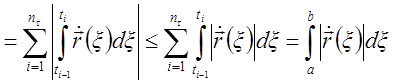 .
.
Таким
образом, 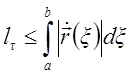 .
Это означает, что кривая
.
Это означает, что кривая ![]() спрямляема, поскольку
спрямляема, поскольку ![]() - ограничена сверху и, следовательно, имеет точную
верхнюю грань, причем
- ограничена сверху и, следовательно, имеет точную
верхнюю грань, причем 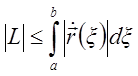 .
.
Пусть
![]() . По
условию функция
. По
условию функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , что эквивалентно непрерывности
функций
, что эквивалентно непрерывности
функций ![]() на
на ![]() .
Тогда по теореме Кантора эти функции, а, следовательно, и
.
Тогда по теореме Кантора эти функции, а, следовательно, и ![]() равномерно непрерывны. Это означает,
что
равномерно непрерывны. Это означает,
что
![]()
![]() .
.
(Заметим,
что, поскольку 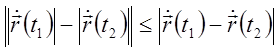 , если выполняется
, если выполняется ![]() , то
, то ![]() ).
).
Рассмотрим произвольное
разбиение ![]() отрезка
отрезка ![]() :
: ![]() .
.
Тогда


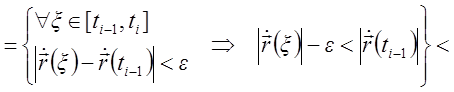
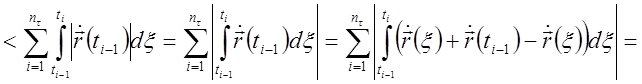
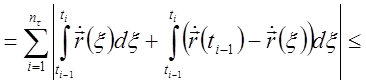

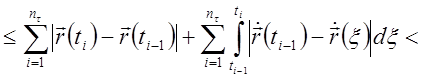
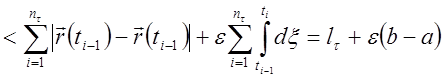 .
.
Итак, 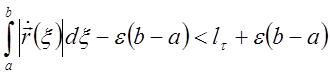 . Отсюда и из ранее доказанного имеем:
. Отсюда и из ранее доказанного имеем:
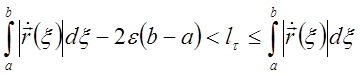 .
.
В силу
произвольности ![]() , это означает
, это означает
 .
.
Таким образом,
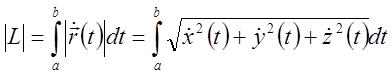 ,
, ![]() .
.
Дифференциал длины дуги
Рассмотрим
функцию 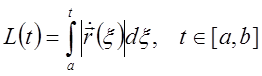 .
.
Очевидно, ![]() есть длина кривой,
соответствующая изменению параметра
есть длина кривой,
соответствующая изменению параметра ![]() на
на ![]() .
.
 .
.
Длина дуги в полярной системе
Пусть ![]() определяется полярным
уравнением
определяется полярным
уравнением ![]() ,
, ![]() . Если функция
. Если функция ![]() непрерывно
дифференцируема на
непрерывно
дифференцируема на ![]() , то кривая
, то кривая ![]() спрямляема и ее длина вычисляется по формуле:
спрямляема и ее длина вычисляется по формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.