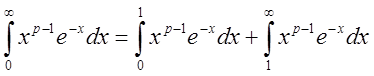 .
.
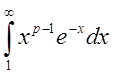 сравним
с
сравним
с 
![]() ,
который, очевидно, сходится.
,
который, очевидно, сходится.
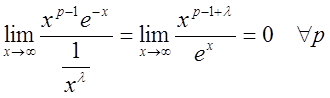 .
.
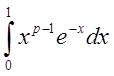 сравним
с
сравним
с 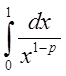 , который сходится при
, который сходится при ![]() и расходится при
и расходится при ![]()
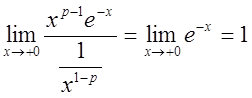 .
.
Следовательно,
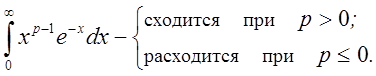
Признак Абеля
Теорема: Пусть
![]() и
и ![]() определены
на
определены
на ![]() и обладают
свойствами:
и обладают
свойствами:
1)![]() - непрерывна и
- непрерывна и 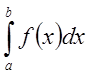 -
сходится;
-
сходится;
2) ![]() - непрерывно –
дифференцируема, ограничена, монотонна.
- непрерывно –
дифференцируема, ограничена, монотонна.
Тогда
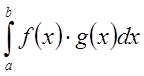 - сходится.
- сходится.
Доказательство:
Из ограниченности функции ![]() следует,
что
следует,
что ![]() . Из сходимости
. Из сходимости 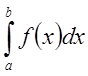 следует,
что
следует,
что ![]()
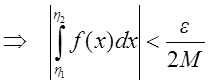 .
.
Имеем при ![]()
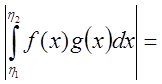 {по второй теореме о среднем}
{по второй теореме о среднем}![]()
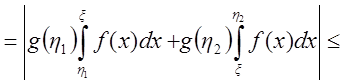
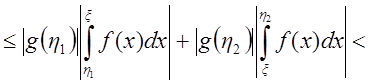
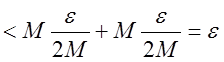 .
.
Тогда по критерию Коши 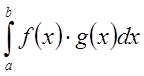 - сходится.
- сходится.
Признак Дирихле
Теорема: Пусть
![]() и
и ![]() определены
на
определены
на ![]() и обладают
свойствами:
и обладают
свойствами:
1)![]() - непрерывна и
- непрерывна и 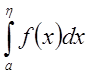 ,
, ![]() - ограниченная функция от
- ограниченная функция от ![]() ;
;
2) ![]() - непрерывно
дифференцируема на
- непрерывно
дифференцируема на ![]() , монотонна и
, монотонна и ![]() .
.
Тогда
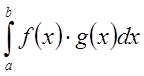 - сходится.
- сходится.
Доказательство:
Пусть все интегралы 
![]() ,
, ![]() .
.
Тогда
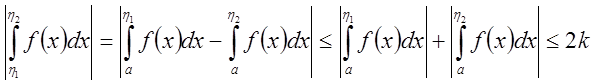
![]() .
.
По условию ![]()
![]()
![]()
![]()
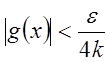 .
.
Пусть
![]() . Тогда
. Тогда
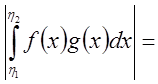 {по второй теореме о среднем}
{по второй теореме о среднем}![]()
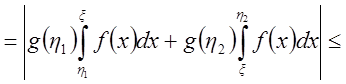
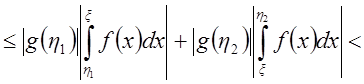
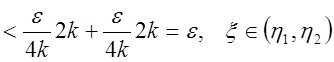
и по критерию Коши 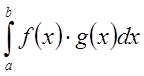 - сходится.
- сходится.
Замечание: Можно показать, что признак Абеля является следствием признака Дирихле.
Примеры:
1.
Исследовать на сходимость интеграл 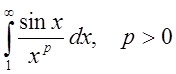 .
.
Решение
Пусть ![]() ,
, 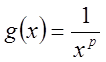 .
.
![]() монотонно убывает и
монотонно убывает и 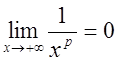 ,
,
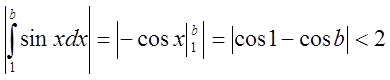 .
.
Условия признака Дирихле выполнены, следовательно,
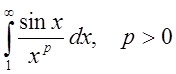 - сходится.
- сходится.
2.
Исследовать на сходимость интеграл 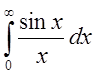 .
.
Решение
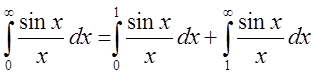 .
.
Из
решения предыдущего примера 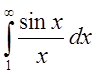 сходится.
сходится.
Так
как функция 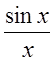 непрерывна на
непрерывна на ![]() , в
точке
, в
точке ![]() ее можно доопределить единицей, поскольку
ее можно доопределить единицей, поскольку
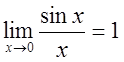 , а также она ограничена, то
, а также она ограничена, то 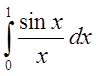 существует.
существует.
Следовательно,
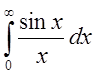 сходится.
сходится.
Теорема:
Если несобственный интеграл 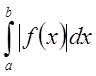 сходится, то сходится
и
сходится, то сходится
и 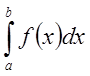 .
.
Доказательство:
Если
интеграл 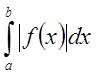 сходится, то в силу критерия Коши
сходится, то в силу критерия Коши ![]()
![]() ,
, ![]()
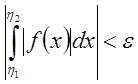 .
.
Но
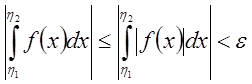 .
.
Тогда
по критерию Коши 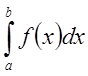 - сходится.
- сходится.
Определение: Несобственный интеграл 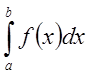 называется абсолютно
сходящимся, если сходится интеграл
называется абсолютно
сходящимся, если сходится интеграл 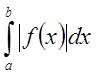 .
.
Заметим,
что обратная теорема не имеет места. Ранее мы показали, что 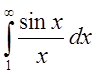 сходится, покажем, что
сходится, покажем, что 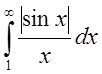 расходится.
расходится.
Очевидно,
![]() .
.
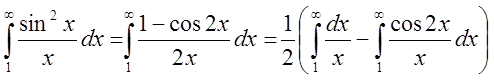 .
.
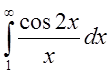 сходится по признаку Дирихле
(доказательство аналогично доказательству для
сходится по признаку Дирихле
(доказательство аналогично доказательству для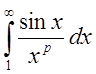 ), а
), а ![]() - расходится.
- расходится.
Следовательно, 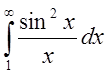 расходится,
и по признаку сравнения расходится
расходится,
и по признаку сравнения расходится 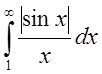 .
.
Определение: В случае, если несобственный интеграл сходится, но не является абсолютно сходящимся, то говорят, что он сходится условно.
Пусть
на ![]() задана функция
задана функция ![]() ,
имеющая особую точку
,
имеющая особую точку ![]() и интегрируема в каждой его
части, не содержащей
и интегрируема в каждой его
части, не содержащей ![]() . Несобственный интеграл от
. Несобственный интеграл от ![]() до
до ![]() определяется
равенством
определяется
равенством
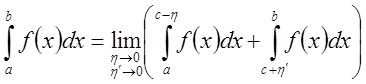
при
независимом предельном переходе по ![]() и
и ![]() .
.
Если
этот предел не существует, то рассматривают предел того же выражения при ![]() . Если такой предел существует, то его
называют (по примеру Коши) главным значением несобственного интеграла
. Если такой предел существует, то его
называют (по примеру Коши) главным значением несобственного интеграла  и обозначают символом
и обозначают символом
V. p. 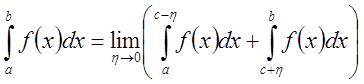 .
.
V. p. – “Valeurprincipale” – “главное значение”.
Заметим, что
если  существует как несобственный, то он,
очевидно, существует и в смысле главного значения; обратное, вообще говоря,
неверно.
существует как несобственный, то он,
очевидно, существует и в смысле главного значения; обратное, вообще говоря,
неверно.
Пример

![]() как несобственный не существует, так как
как несобственный не существует, так как 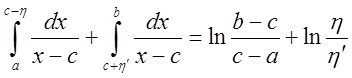 - не имеет определенного предела,
если
- не имеет определенного предела,
если![]() и
и ![]() ,
независимо друг от друга.
,
независимо друг от друга.
Если
же ![]() , то
, то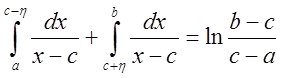 - то
получим выражение, не зависящее от
- то
получим выражение, не зависящее от ![]() . Таким образом,
главное значение интеграла существует:
. Таким образом,
главное значение интеграла существует:
V. p. 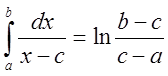 .
.
Понятие
главного значения можно распространить и на случай нескольких особых точек
(конечного числа) внутри промежутка, а также на случай промежутка ![]() , не имеющего внутри особых точек
, не имеющего внутри особых точек
V. p.  .
.
СОДЕРЖАНИЕ
1. Неопределенный интеграл. 4
1.1. Первообразная и неопределенный интеграл. 4
1.2. Основные свойства неопределенного интеграла. 4
1.3. Таблица основных неопределенных интегралов. 5
1.4. Основные методы интегрирования. 6
1.4.1. Метод замены переменной (подстановки) 6
1.4.2. Интегрирование по частям.. 8
1.5. Интегрирование рациональных дробей. 9
1.5.1. Разложение рациональной дроби на простейшие. 9
1.5.2. Интегрирование простейших дробей. 11
1.5.3. Метод Остроградского. 12
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.