Очевидно,
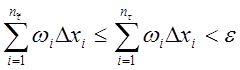 . Разбиение
. Разбиение ![]() отрезка
отрезка
![]() порождает разбиение
порождает разбиение ![]() отрезка
отрезка ![]() , причем
, причем
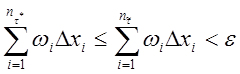 , т.к. каждое слагаемое первой суммы является
также слагаемым и второй суммы.
, т.к. каждое слагаемое первой суммы является
также слагаемым и второй суммы.
Это
означает, что ![]() .
.
40. Если ![]() и
и ![]() , то
, то ![]() , причем
, причем
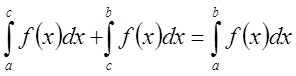 .
(*)
.
(*)
Справедливо также и обратное утверждение:
если ![]() , то
, то ![]() и
и ![]()
![]() и выполняется (*).
и выполняется (*).
Доказательство:
Пусть
![]() и
и ![]() ,
следовательно
,
следовательно ![]() отрезка
отрезка ![]() отрезка
отрезка
![]() такие, что
такие, что 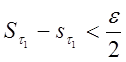 и
и 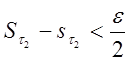 . Тогда для
. Тогда для ![]() отрезка
отрезка
![]() имеем
имеем
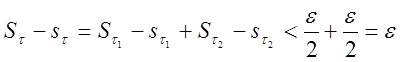 ,
,
следовательно ![]() .
.
Докажем равенство (*).
Пусть
![]() и
и ![]() -
произвольные разбиения отрезков
-
произвольные разбиения отрезков ![]() и
и ![]() соответственно и
соответственно и ![]() .
.
Очевидно,
![]() ,
, ![]() ,
, ![]() , если
, если ![]() то
то ![]() и наоборот. Переходя к пределу в последнем
равенстве, получим
и наоборот. Переходя к пределу в последнем
равенстве, получим
![]()
или
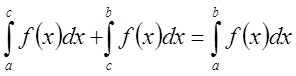 .
.
Замечание:
Можно показать, что равенство (*)
имеет место и в том случае, когда ![]() .
.
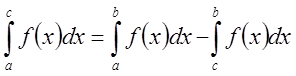
![]()
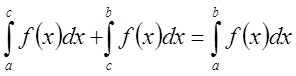 .
.
50. Если функция ![]() на
на
![]() за исключением конечного числа точек, то
за исключением конечного числа точек, то ![]() и
и 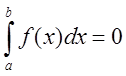 .
.
Доказательство:
Очевидно, что ![]() имеет на
имеет на ![]() конечное число точек
разрыва, поэтому по доказанному ранее
конечное число точек
разрыва, поэтому по доказанному ранее ![]() .
.
Пусть ![]() - произвольное
разбиение отрезка
- произвольное
разбиение отрезка ![]() и
и ![]() -
множество промежуточных точек, таких, что
-
множество промежуточных точек, таких, что ![]() , т.е.
ни одна из точек
, т.е.
ни одна из точек ![]() не совпадает с точкой разрыва.
не совпадает с точкой разрыва.
Составим интегральную сумму
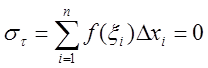 .
.
Переходя к пределу при ![]() ,
получим
,
получим
![]()
![]()
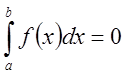 .
.
60. Если
функцию![]() изменить в конечном числе точек, то
полученная функция будет интегрируемой на
изменить в конечном числе точек, то
полученная функция будет интегрируемой на ![]() и
интеграл ее не изменится.
и
интеграл ее не изменится.
Доказательство:
Пусть ![]() - функция, измененная в
конечном числе точек отрезка
- функция, измененная в
конечном числе точек отрезка ![]() . Рассмотрим
. Рассмотрим ![]() , (за исключением конечного числа точек).
Тогда
, (за исключением конечного числа точек).
Тогда ![]() по предыдущему свойству и
по предыдущему свойству и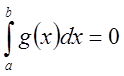 .
.
![]()
![]()
![]()
и
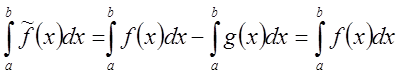 .
.
70.Если ![]() ,
то и
,
то и ![]() .
.
Доказательство:
В
силу интегрируемости функций ![]() и
и ![]() на
на ![]() , они
ограничены на нем, т.е. существуют
, они
ограничены на нем, т.е. существуют ![]() , такие, что
, такие, что ![]() ,
, ![]()
![]() . Следовательно,
. Следовательно, ![]() также
ограничено, т.к.
также
ограничено, т.к. ![]() .
.
Пусть
![]() - произвольное разбиение отрезка
- произвольное разбиение отрезка ![]() . Оценим выражение
. Оценим выражение ![]() ,
где
,
где ![]() и
и ![]() .
.
![]()
![]()
![]() .
.
Учитывая
![]() ,
, ![]() и
последнее равенство, имеем
и
последнее равенство, имеем
![]() ,
,
где ![]() и
и
![]() - колебания функций
- колебания функций ![]() и
и ![]() на
на ![]() .
.
Из
последнего неравенства для колебания произведения ![]() на
отрезке
на
отрезке ![]() имеем
имеем ![]() ,
следовательно
,
следовательно
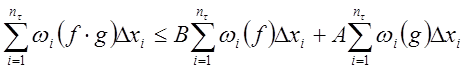 .
.
В силу
интегрируемости функций ![]() и
и ![]() имеем
имеем
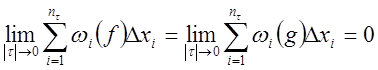
![]()
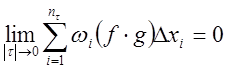 .
.
Следовательно,
![]() .
.
80.Пусть ![]() ,
причем
,
причем ![]() . Тогда
. Тогда 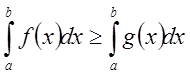 .
.
Доказательство:
Для
произвольного разбиения ![]() и произвольных точек
и произвольных точек
![]() имеем
имеем
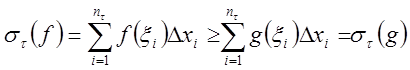 .
.
Переходя
к пределу при ![]() , получим
, получим 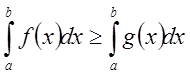 .
.
90. Если
![]() , то и
, то и ![]() ,
причем
,
причем 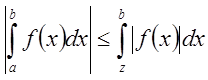 ,
, ![]() .
.
Доказательство:
![]()
![]()
![]() - ограничена
- ограничена ![]()
![]() - ограничена на
- ограничена на ![]() .
.
![]() ,
очевидно, имеет место неравенство
,
очевидно, имеет место неравенство
![]() .
.
Пусть ![]() - произвольное разбиение отрезка
- произвольное разбиение отрезка ![]() ;
; ![]() и
и ![]() - колебания функций
- колебания функций ![]() и
и ![]() на
отрезке
на
отрезке ![]() .
.
Тогда для
точек ![]() имеем
имеем
![]()
![]() .
.
Поэтому
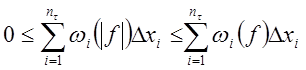 .
.
Отсюда,
поскольку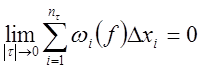 , то и
, то и 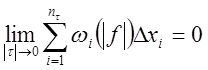 , а
это значит, что
, а
это значит, что ![]() .
.
Пусть ![]() . Тогда
. Тогда 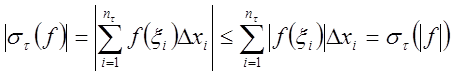 .
Переходя в этом неравенстве к пределу при
.
Переходя в этом неравенстве к пределу при ![]() и
замечая, что
и
замечая, что
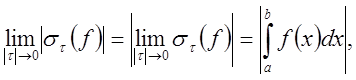
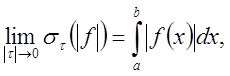
получим
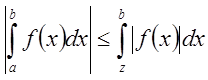 ,
, ![]() .
.
Теорема
1: Пусть функции![]() , причем
, причем ![]() –
неотрицательная (неположительная) на
–
неотрицательная (неположительная) на ![]() и
и ![]() ,
, ![]() .
.
Тогда 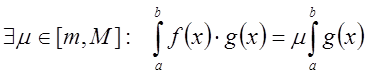 .
.
Доказательство:
Предположим,
для определенности, что ![]() . Тогда, умножая
неравенство
. Тогда, умножая
неравенство ![]() на
на ![]() ,
получим
,
получим
![]()
![]() . (*)
. (*)
По
свойству 8: 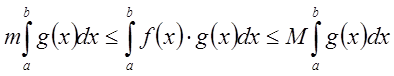 .
.
Так
как 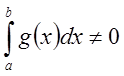 , то
, то 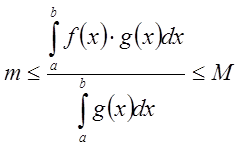 ,
,
и полагая, 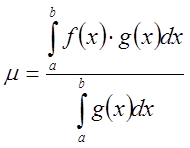 , получим отсюда
, получим отсюда
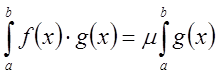 .
.
Если
же 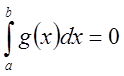 , то из (*) следует, что
, то из (*) следует, что 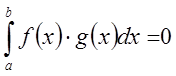 и
и
![]() - любое число из
- любое число из ![]() .
.
Следствие
1: Если ![]() –
непрерывная функция на
–
непрерывная функция на ![]() , а
, а ![]() –
неотрицательная (неположительная) и
–
неотрицательная (неположительная) и ![]() , то
, то 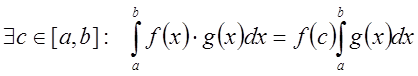 .
.
Доказательство:
Пусть ![]() и
и ![]() .
.
В
силу непрерывности функции ![]() , она принимает все
значения на
, она принимает все
значения на ![]() , следовательно, найдется точка
, следовательно, найдется точка ![]() ,
, ![]() . Тогда
из предыдущей теоремы следует справедливость доказываемого утверждения.
. Тогда
из предыдущей теоремы следует справедливость доказываемого утверждения.
Определение: Пусть![]() .
.
Число 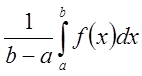 называется интегральным средним
значением функции
называется интегральным средним
значением функции ![]() на
на ![]() .
.
Следствие
2: (об интегральном среднем для
непрерывных функций)Если ![]() – непрерывная на
– непрерывная на ![]() функция, то ее интегральное среднее на
этом отрезке равно значению функции в некоторой точке, т.е.
функция, то ее интегральное среднее на
этом отрезке равно значению функции в некоторой точке, т.е.
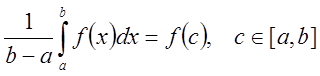 .
.
Доказательство:
Пусть![]() .
.
Из следствия 1 имеем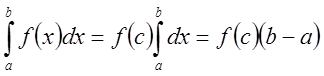
![]()
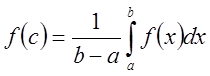 ,
, ![]() .
.
Пусть![]() , тогда
, тогда ![]() .
Рассмотрим определенную на
.
Рассмотрим определенную на ![]() функцию
функцию
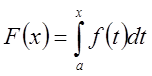 ,
,
которая называется интегралом с переменным верхним пределом.
Теорема
1: Функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() .
.
Доказательство:
Пусть
![]() произвольная точка из
произвольная точка из ![]() и
и ![]() .
.
Рассмотрим
приращение функции ![]() в точке
в точке ![]()
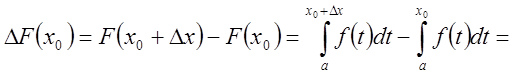
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.