Математический анализ: Курс лекций (часть вторая "Интегральное исчисление функции одной переменной"), страница 14

Причем, если хотя бы один из интегралов, стоящих в правой части последнего равенства расходится, то расходится и интеграл, стоящий в левой части.

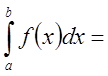{ - неограниченна в точках  и }

 , .

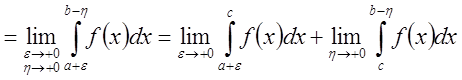Причем, если хотя бы один из интегралов, стоящих в правой части последнего равенства расходится, то расходится и интеграл, стоящий в левой части.

              Примеры:

1.  Исследовать на сходимость интеграл  .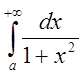

Решение

.

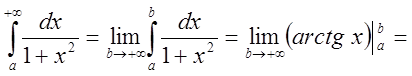
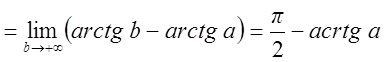Интеграл сходится.

2.  Исследовать на сходимость интеграл  .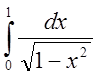

              Решение

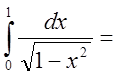{подынтегральная функция в т.  неограниченна}

.

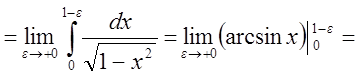
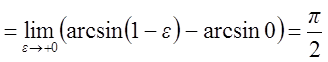Интеграл сходится.

3.  Исследовать на сходимость интеграл  .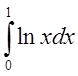

              Решение

.

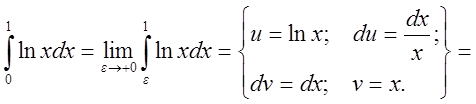
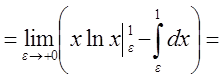
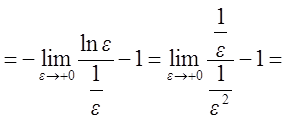
Интеграл сходится.

4.  Исследовать на сходимость интеграл  .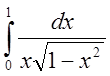

              Решение

 

;

;

.

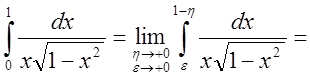
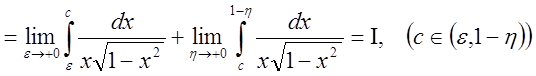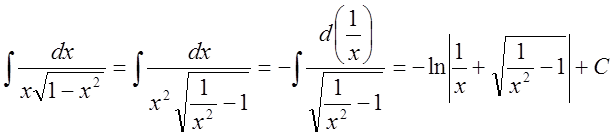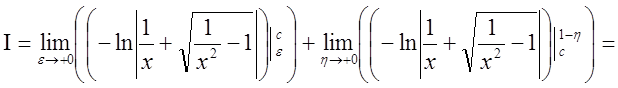
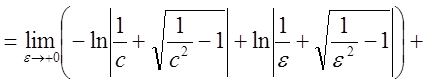
Интеграл расходится.

5.  Основной пример

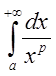
5. 1.  При каких  интеграл   сходится?

              Решение

.

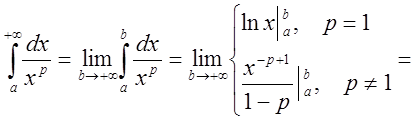
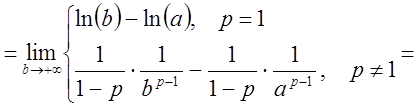
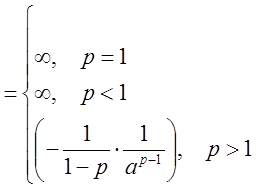              Имеем: 

.

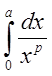
5. 2.  При каких  интеграл   сходится?

              Решение

.

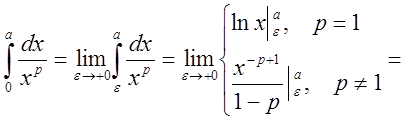
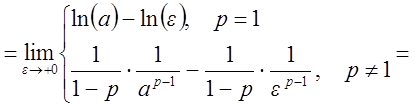
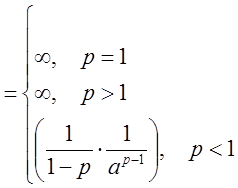Имеем: 

.

5. 3.  Аналогично можно показать:

,

.

3.1. Критерий Коши сходимости несобственных интегралов

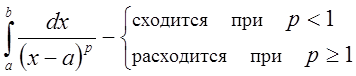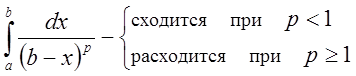Теорема: Пусть функция  определена на промежутке ,  и интегрируема по Риману на , . Для того чтобы несобственный интеграл 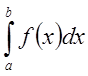 сходился, необходимо и достаточно, чтобы

.

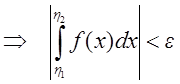Доказательство:

Рассмотрим функцию 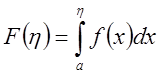, . Для того чтобы эта функция имела предел при , необходимо и достаточно, чтобы 

,

 (критерий Коши существования предела функции).

Но

.

.

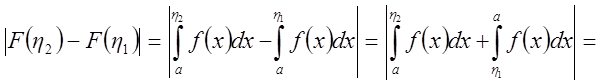
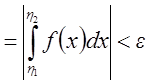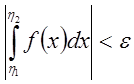А  .

€

3.2. Признаки сходимости несобственных интегралов

3.2.1. Сходимость интегралов

от  неотрицательных функций

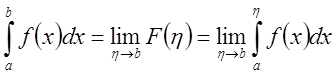Теорема:  Пусть функция  неотрицательна на промежутке ,  и интегрируема на любом отрезке , . Для того чтобы 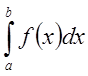 сходился, необходимо и достаточно, чтобы функция 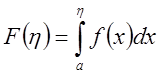 была ограниченна сверху на . В случае выполнения этого условия

.

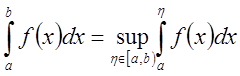Доказательство:

Рассмотрим функцию 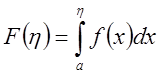, . В силу того, что , функция  не убывает.

В самом деле, если , то

.

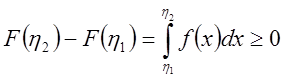Несобственный интегра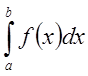л  сходится, тогда и только тогда, когда существует конечный предел

,

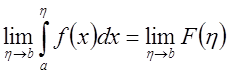а последний существует тогда и только тогда, когда функция ограничена сверху, (из теоремы о пределе монотонной функции) и при этом

.

€

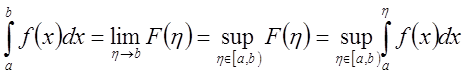Признак сравнения

              Теорема: Пусть функции  и  неотрицательны на  и интегрируемы на любом отрезке , . Пусть   (в частности).

Тогда:

1)  если 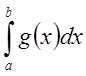 - сходится, то сходится и ;

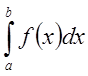2)  если 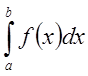 - расходится, то расходится и .

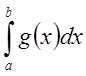Доказательство:

1) Пусть 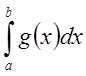  - сходится, тогда по доказанной выше теореме , .

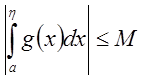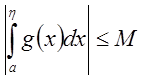Из  следует, что   выполняется неравенство . Из следует, что .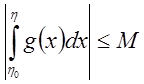

Следовательно, .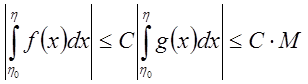

              По доказанной выше теореме 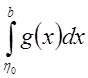, а, следовательно, и  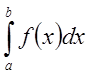- сходятся.

              2) Если 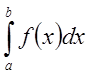 - расходится, то очевидно расходится и интеграл 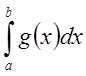, так как в противном случае по доказанному 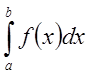 - сходился бы.

              Следствие: (предельная форма признака сравнения)

              Пусть функции  и  неотрицательны на  и интегрируемы на любом отрезке , ,  и существует  .

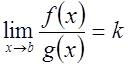 Тогда:

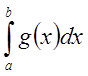1) Если , то из сходимости  следует сходимость .

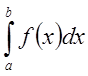2) Если , то из расходимости 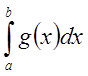 следует расходимость .

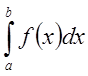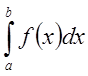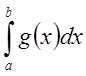В частности если  - число отличное от нуля, то интегралы   и  - сходятся или расходятся одновременно.

Доказательство:

1) Пусть . Тогда из 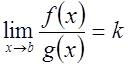    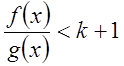, т.е. . Это означает, что  , и утверждение 1) следствия следует из 1) признака сравнения. 

              2)  Пусть . Тогда из 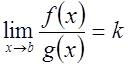     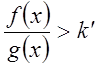 или 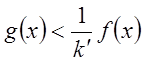. Это означает, что  ,  и  утверждение 2) следует из 2) признака сравнения.

              Примеры:

1.  Исследовать на сходимость интеграл  .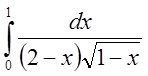

              Решение

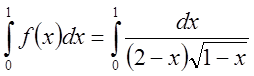 сравним с .

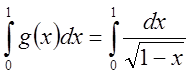Известно, что 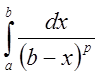 сходится при  и расходится при .

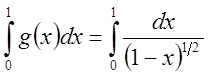 - сходится т.к. .

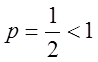              Поскольку 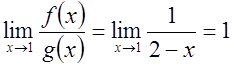 , то по следствию из признака сравнения

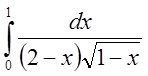 - сходится.

2.  Исследовать на сходимость интеграл  .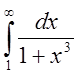

              Решение

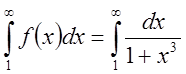 сравним с .

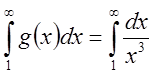Известно, что 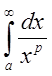 сходится при  и расходится при .

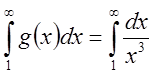 - сходится, т.к. .

              Поскольку 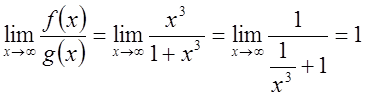 ,  то по следствию из признака сравнения  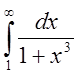 - сходится.

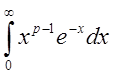3.  Определить, при каких интеграл   сходится, а при каких - расходится.

              Решение