Дано: m = 0,10 кг – масса шарика, κ = 10 Н/м – жесткость пружины, φ0 = 0 – начальная фаза колебаний, t1 = 52,36×10-3 с и t2 = Т/6 – промежутки времени, прошедшие от начала колебаний, А = 4,0×10-2 м – амплитуда колебаний. Найти:х1 – смещение шарика к моменту времени t1; W – полную энергию колебательного движения; Ек0 – кинетическую энергию в момент прохождения положения равновесия; Ек2 – кинетическую и Еn2 – потенциальную энергию колебательного движения в момент времени t2 = Т/6.
Решение: 1) Смещение при гармонических колебаниях определяется по формуле
Х = Аsin(ωt + φ0) или х = Аsin(2π/Т×t + φ0)
Так как по условию φ0 = 0 ,то
х = Аsin(2π/Т · t)
Период
упругих гармонических колебаний определяется соотношением Т = 2π 
, где m – масса
колеблющегося тела. Находим смещение х1 по формуле
х 1= Аsin(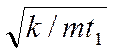
),
x1 = 4,0×10-2 м×sin(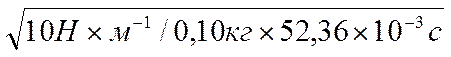
) =
= 4,0×10-2 м×sin(0,5236 рад) ≈ 2×10-2 м
2) Полную энергию колебательного движения определяем по формуле
W = ½ kA2
Так как в момент прохождения положения равновесия вся энергия колебательного движения переходит в кинетическую, то
Ек0 = W = ½ kA2 = ½ mυ02
Вычисляем полную энергию колебательного движения и равную ей максимальную кинетическую энергию колеблющейся материальной точки:
W = ½×10Н/м×(4,0×10-2 м)2 = 8,0×10-3 Дж
3) Кинетическую энергию шарика находим из формулы
Ек = ½ mυ02 ×cos2φ,
где υ = mυ0 сos φ – мгновенное значение скорости, υ0 – максимальная скорость,
φ = (2π/Т)t + φ0 – фаза колебаний. По условию начальная фаза равна нулю, и , значит, φ = (2π/Т)t. Так как ½ mυ02 = W – полная энергия (см. пункт 2), то
Ек = ½ mυ02cos2 φ = ½ kA2 cos2 φ = W cos2 φ
Учитывая значение φ получаем
Ек2 = ½ kA2 cos2(2π/Т×t2) = W cos2(2π/Т×t2) = W cos2π/3
Для потенциальной энергии в момент времени t2 имеем
En2 = 1/2кх22 = ½ кА2sin2 φ = W sin2 φ,
где х2 = А sinφ. В данном случае
Еn2 = ½ кА2sin2(2π/Т×t2) = W sin2(2π/Т×t2)
Потенциальную энергию можно найти из закона сохранения энергии
Еп2 = W – Ek2.
Подставляя числовые значения, определяем кинетическую и потенциальную энергию в момент времени t2:
Ек2 = 8,0×10-3 Дж ×¼ = 2,0×10-3 Дж,
Еп2 = 8,0×10-3 Дж - 2,0×10-3 Дж = 6,0×10-3 Дж
Ответ: 1) Смещение шарика от положения равновесия приблизительно равно 2×10-2 м; 2) полная энергия колебательного движения равна 8,0×10-3 Дж; 3) в момент времени t2 кинетическая энергия шарика равна 2,0×10-3 Дж, потенциальная энергия равна 6,0×10-3 Дж
Пример 55. Кабина, к потолку которой подвешен математический маятник длиной в 1,0 м, начинает опускаться вертикально вниз с ускорением а1 = g/4. Спустя время t1 = 3,0 с после начала движения кабина начинает двигаться равномерно, а затем в течение 3,0 с тормозится до остановки.
Определить: 1) период гармонических колебаний маятника на каждом из участков пути; 2) период гармонических колебаний маятника при движении точки подвеса в горизонтальном направлении с ускорением а4 = g/4.
Дано: а1 = g/4 – ускорение кабины на первом участке пути, t1 = 3,0 с – время движения на первом участке пути, υ2 = сonst – скорость кабины на втором участке пути, t3= 3,0 – время движения на третьем участке пути, υ3 = 0 – скорость кабины в конце третьего участка пути, а4 = g/4 – ускорение точки подвеса на горизонтальном участке пути, g ≈ 9,8 м/с2 – ускорение свободного падения, l = 1,0 м – длина маятника. Найти: Т1, Т2, Т3 - периоды колебаний маятника на соответствующих участках пути, Т4 – период колебаний при горизонтальном движении точки подвеса.
Решение.
Период гармонических колебаний математического маятника определяется по формуле
Т = 2π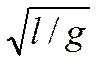
При равнопеременном движении точки
подвеса период колебаний определяется по формуле Т = 2π
,
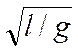где ускорение маятника g′ можно найти из соотношения g′ = g + а. Вектор а равен
по модулю вектору ускорения токи подвеса и противоположен ему по направлению.
При движении точки подвеса вниз с ускорением а1 рисунок 55 а ускорение
маятника g′1 = g – а1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.