де 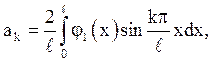
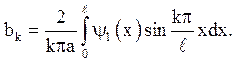
Для вирішення задачі (4.12) доцільно застосувати наступні дії.
Третій етап. Рішення
задачі (4.12) шукається у вигляді ряду по власних функціях ![]() задачі (4.11):
задачі (4.11):
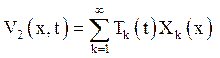 (4.14)
(4.14)
з невідомими функціями ![]() .
.
В даному випадку:
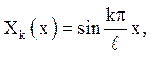
![]() (4.15)
(4.15)
(слід помітити, що в інших задачах власні функції
можуть бути іншими). Підставивши ![]() з (4.14) в неоднорідне рівняння, легко отримати
з (4.14) в неоднорідне рівняння, легко отримати
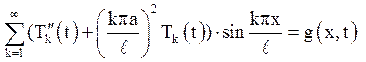
або
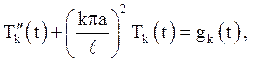 (4.16)
(4.16)
де ![]() – коефіцієнти Фур’є функції
– коефіцієнти Фур’є функції ![]() :
:
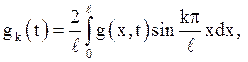 (4.17)
(4.17)
З нульових початкових умов задачі (4.12) через уявлення (4.14) виходить, що
![]()
![]() (4.18)
(4.18)
отже рівняння (4.16) потрібно вирішувати за граничних умов (4.18). Рішення неоднорідного рівняння (4.16) прийнято шукати у вигляді
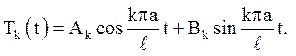
Тут ![]() і
і ![]() – невідомі функції. Відповідно до
методу варіації постійних слід вирішити систему
– невідомі функції. Відповідно до
методу варіації постійних слід вирішити систему
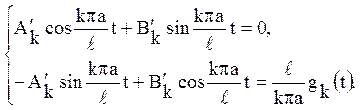
Звідси
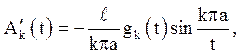
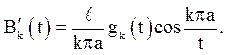
Отже
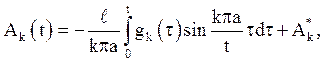
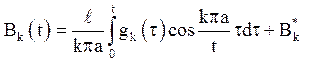
де ![]()
![]() –
постійні.
–
постійні.
Значить, загальне рішення рівняння (4.16) має вигляд:
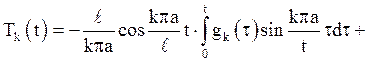
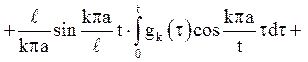
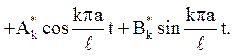
З умов (4.18)
виходить, що ![]() тоді рішенню задачі (4.16)-(4.18) після елементарних
перетворень можна додати вигляд:
тоді рішенню задачі (4.16)-(4.18) після елементарних
перетворень можна додати вигляд:
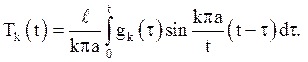 (4.19)
(4.19)
(Це рішення можна було швидше отримати, застосувавши перетворення Лапласа). Підставляючи знайдені функції (4.19) і власні функції (4.15) в уявлення (4.14), можна отримати:
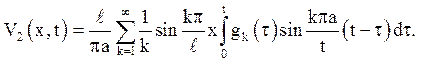 (4.20)
(4.20)
Сума функцій (4.9), (4.13) і (4.20) дасть остаточне рішення задачі (4.8):
![]() (4.21)
(4.21)
Приклад 1. Однорідна струна завдовжки l, закріплена на кінцях ![]() і
і ![]() , коливається під дією зовнішньої гармонійної сили
, коливається під дією зовнішньої гармонійної сили ![]() розрахованої на одиницю довжини. Знайти відхилення
розрахованої на одиницю довжини. Знайти відхилення
![]() струни за довільних початкових умов.
Досліджувати можливість резонансу і знайти рішення у разі резонансу.
струни за довільних початкових умов.
Досліджувати можливість резонансу і знайти рішення у разі резонансу.
Потрібно вирішити задачу:
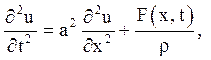
![]()
![]()
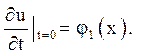
Рішення слідує шукати у вигляді суми ![]() Тут V(x,t)- рішення задачі, розглянутої в розд. 3:
Тут V(x,t)- рішення задачі, розглянутої в розд. 3:
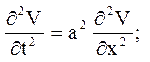
![]()
![]()
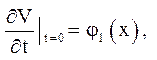
а W(x,t)- рішення задачі з неоднорідністю тільки в рівнянні:
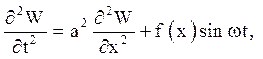
![]()
![]()
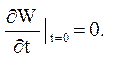
Рішення задачі для V(x,t) дається формулою (4.13), а функцію W(x,t) можна представити у вигляді:
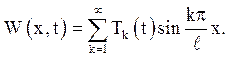
Невідомі функції Tk(t)
задовольняють рівнянь (4.16), де gk(t) коефіцієнти Фур’є правої
частини ![]() тобто
тобто
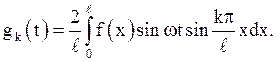
Якщо позначити
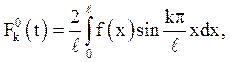 то
то ![]()
Значить, функція Tk(t) задовольняє рівнянню
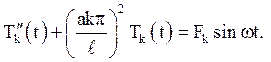 (4.22)
(4.22)
із умов ![]()
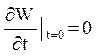 виходить, що
виходить, що
![]()
![]() (4.23)
(4.23)
Рішення неоднорідного
рівняння (4.22) із спеціальною правою частиною традиційно розшукується у
вигляді суми ![]() де
де 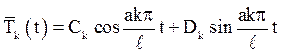 – загальне рішення однорідного рівняння, а приватне
рішення неоднорідного рівняння
– загальне рішення однорідного рівняння, а приватне
рішення неоднорідного рівняння ![]() можна знайти по виду правої частини.
можна знайти по виду правої частини.
Далі розглядаються два випадки:
1) Немає резонансу, тобто частота w
вимушених коливань не співпадає ні з однією з частот 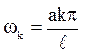 власних коливань. Приватне рішення
неоднорідного рівняння слід шукати у вигляді
власних коливань. Приватне рішення
неоднорідного рівняння слід шукати у вигляді
![]()
Тоді
![]()
![]()
Підставимо в рівняння(4.22)
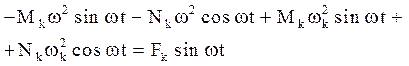
і прирівняємо коефіцієнти при ![]() і при cos(wt):
і при cos(wt):
![]() ;
;
![]()
і отримаємо 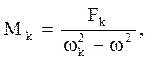
![]()
Знайшли приватне рішення
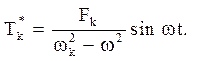
Загальне рішення неоднорідного рівняння (4.22) приймає вигляд:
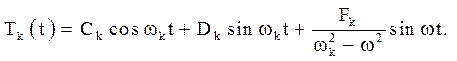
Коефіцієнти Ск
і Dk визначаються з умов (4.23). Перше з них дає ![]() . Щоб задовольнити другому, слід продиференціювати
функцію
. Щоб задовольнити другому, слід продиференціювати
функцію ![]() :
:
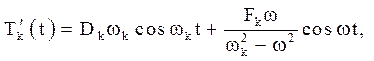
що при ![]() приводить до залежності:
приводить до залежності: 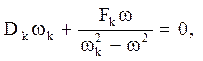 звідки
звідки
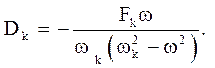
Значить, рішення задачі (4.22)-(4.23) за відсутності резонансу має вигляд:
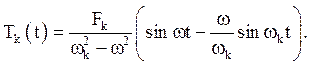
Тоді
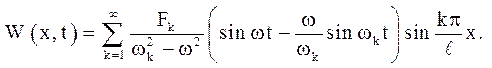 (4.24)
(4.24)
2) Резонансний
випадок. Тут важливо пам'ятати, що резонанс виникає, коли частота w зовнішньої сили що вимушує співпадає з однією з
частот 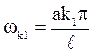 власних коливань.
власних коливань.
Тоді для всіх ![]() немає резонансу, значить
немає резонансу, значить
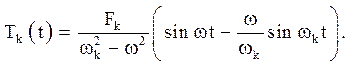
Для ![]() функція Тк1 є рішення задачі
(4.22)-(4.23), розшукуване у вигляді
функція Тк1 є рішення задачі
(4.22)-(4.23), розшукуване у вигляді ![]() де як і раніше
де як і раніше ![]() а приватне рішення неоднорідного рівняння через
резонанс має вигляд:
а приватне рішення неоднорідного рівняння через
резонанс має вигляд:
![]()
Тоді
![]()
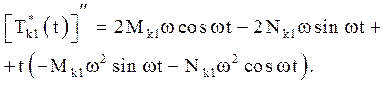
Ці похідні слідує підставимо в рівняння (4.22):
![]()
![]()
Оскільки ![]() після приведення подібних отримаємо
після приведення подібних отримаємо
![]()
Звідси
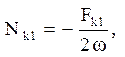
![]()
тобто знайшли приватне рішення
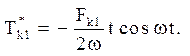
Отже, загальне рішення неоднорідного рівняння (4.22) приймає вигляд:
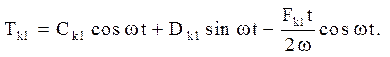
Перша з початкових
умов (4.23) дає ![]() ;
після обчислення похідної
;
після обчислення похідної
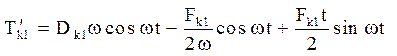
при ![]() виходить
виходить 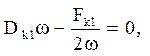 звідки
звідки 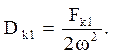
Значит,
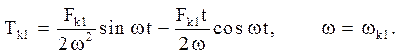
Отже, у разі резонансу
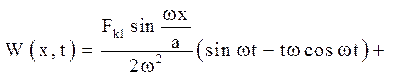
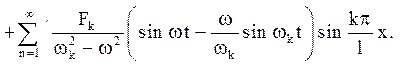 (4.25)
(4.25)
Тут знак "штрих" указує, що при підсумовуванні потрібно пропустити
доданок з індексом ![]() .
.
Залишилося скласти функції (4.13) і (4.24) за відсутності резонансу або (4.13) і (4.25) у разі резонансу.
1. На струну завдовжки ![]() постійно
діє зовнішня збудлива сила, густина якої (в розрахунку, на одиницю
аси струни), рівна
постійно
діє зовнішня збудлива сила, густина якої (в розрахунку, на одиницю
аси струни), рівна 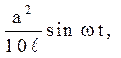 де а – постійна, фігуруюча в рівнянні струни w – дане
позитивне число, відмінне від всіх чисел вигляду
де а – постійна, фігуруюча в рівнянні струни w – дане
позитивне число, відмінне від всіх чисел вигляду 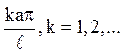 Знайти закон коливання струни, якщо початкове
відхилення і початкова швидкість рівне нулю, а кінці струни закріплені.
Знайти закон коливання струни, якщо початкове
відхилення і початкова швидкість рівне нулю, а кінці струни закріплені.
Відповідь:
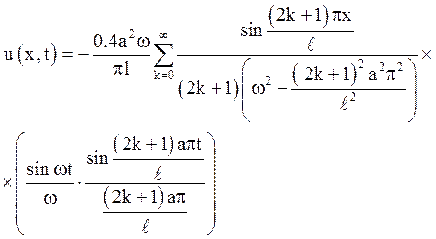
2. На струну завдовжки ![]() постійно діє
зовнішня вимушуюча сила, рівна (з розрахунку на одиницю маси струни)
постійно діє
зовнішня вимушуюча сила, рівна (з розрахунку на одиницю маси струни) 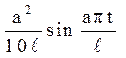 ; тут а –
постійна, яка фігурує в рівнянні коливання струни. Знайти закон коливання
струни, якщо початкове відхилення і початкова швидкість рівне нулю, а кінці
струни закріплені.
; тут а –
постійна, яка фігурує в рівнянні коливання струни. Знайти закон коливання
струни, якщо початкове відхилення і початкова швидкість рівне нулю, а кінці
струни закріплені.
Відповідь:
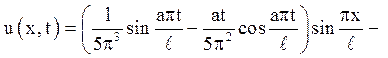
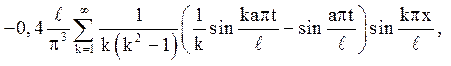
де підсумовування поширено на все непарні ![]()
3. На відрізку ![]()
![]() вирішити рівняння
вирішити рівняння ![]() за нульових початкових умов. Кінці струни
закріплені.
за нульових початкових умов. Кінці струни
закріплені.
Відповідь:
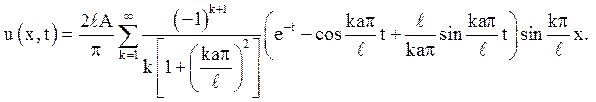
4. Лівий кінець струни рухається згідно із
законом 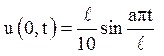 (де а – постійна в рівнянні коливання струни,
(де а – постійна в рівнянні коливання струни, ![]() –
довжина струни), а правий закріплений:
–
довжина струни), а правий закріплений: ![]() . Знайти закон коливання цієї струни, якщо зовнішня обурююча сила,
початкове відхилення і початкова швидкість рівне нулю.
. Знайти закон коливання цієї струни, якщо зовнішня обурююча сила,
початкове відхилення і початкова швидкість рівне нулю.
Відповідь:
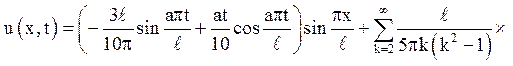
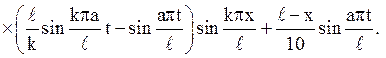
Це рішення можна
записати також в іншій формі, якщо в останньому доданку замінити 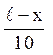 його розкладанням в ряд по синусах:
його розкладанням в ряд по синусах:
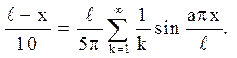
Тоді
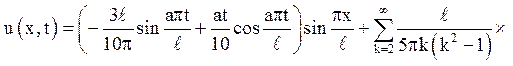
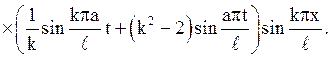
5. Вирішити рівняння
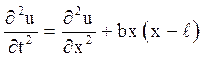
за нульових початкових і крайових умов ![]()
![]()
Відповідь:
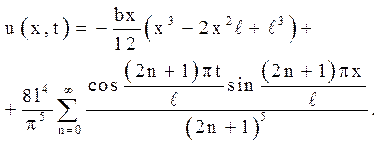
6. Решить уравнение
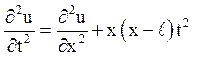
за нульових початкових і крайових умов ![]()
![]()
Відповідь:
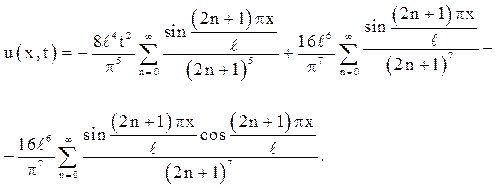
1. Спочатку розглядається задача про вільні коливання струни (стрижня) з двома вільними кінцями:
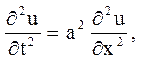
![]()
![]() (5.1)
(5.1)
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.