де введена нова постійна ak=СkAk. Залишилося підсумовувати рішення uk(x,t):
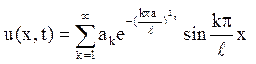 (8.5)
(8.5)
і визначити постійні ак так, щоб функція u(x,t) задовольняла заданій початковій умові
u(x,0) =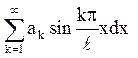 (8.6)
(8.6)
Формула (8.6) показує, що ак є коефіцієнт розкладання функції j(х) в ряд Фур’є по синусах на (0,l), тобто
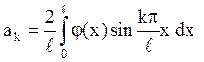
Рішення неоднорідних задач теплопровідності
Розглянемо застосування етапів 1-3 (див. розділ 4) для різних неоднорідних задач про розповсюдження тепла в стрижні на конкретних прикладах. При цьому звернемо увагу на деякі спрощення в окремому випадку джерел стаціонарної потужності згідно етапу 4 (див. розділ 6).
Приклад 1. ( Із заданим режимом на кінцях)
Даний тонкий однорідний стрижень завдовжки l, початкова температура якого рівна нулю. На кінці х = l температура підтримується рівній нулю, а на кінці х = 0 вона росте лінійно з часом, так що u(0,t)= At, де А – постійна. Знайти розподіл температури уздовж стрижня при t > 0.
Рішення. Функція u(x, t) є рішення задачі
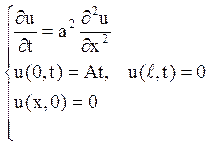
Згідно етапу 1 будуємо допоміжну функцію m(x,t), що задовольняє крайовим умовам. Це лінійна функція, що проходить через точки (0, А t) і (l,0):
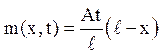
Шукаємо рішення у вигляді
U(x,t)= m(x,t)+ ![]() (x,t)
(x,t)
Де для нової
невідомої функції ![]() (x,t) одержуємо задачу
(x,t) одержуємо задачу
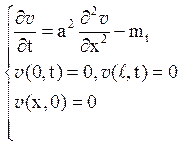
Тут
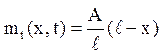
Рішення цієї задачі із стаціонарною неоднорідністю в рівнянні згідно етапу 4 шукаємо у вигляді
![]() (x,t) =
(x,t) = ![]() 1(x,t)+
1(x,t)+ ![]() 2(x)
2(x)
де функцію ![]() 2 (x) підбираємо так, щоб
2 (x) підбираємо так, щоб
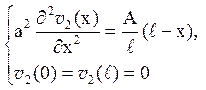
Знаходимо загальне рішення
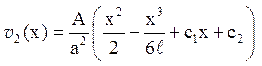
і з крайових умов визначаємо с1=-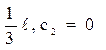 . Значить
. Значить
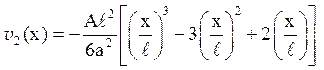
Для функції v1(x,t) одержуємо задачу
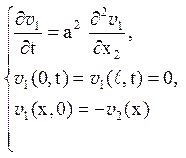
Ця задача вирішена методом Фур’є в попередньому параграфі. Запишемо їх рішення:
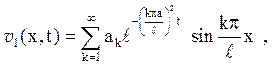
де
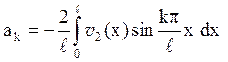
Обчислимо інтеграл по частинах, вважаючи
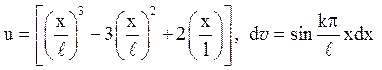
Отримаємо:
ak=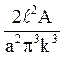 .
.
Значить, функція ![]() 1(x,t) має вигляд
1(x,t) має вигляд
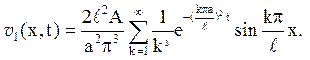
Щоб отримати
відповідь, треба скласти знайдені функції m(x,t), ![]() 1(x,t),
1(x,t), ![]() 2(x,t)
2(x,t)
Відповідь:
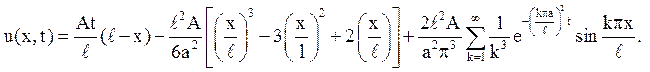
Приклад 2. (Із заданим режимом на одному кінці стрижня і тепла на іншому)
Даний тонкий однорідний стрижень завдовжки l, бічна поверхня якого теплоізольована. Початкова температура стрижня відома. Кінець стрижня х=0 підтримується при температурі, рівній нулю, а на кінці х =l відбувається теплообмін з навколишнім середовищем, температура якого вважається рівною нулю. Визначити температуру стрижня при t > 0.
Рішення. Треба вирішити задачу.
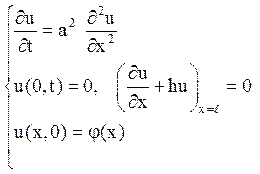
Слідуючи методу Фур’є, шукаємо рішення у вигляді
U(x,t)= X(x) T(t)
Для функції X(x) приходимо до задачі
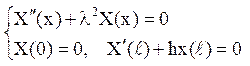
Загальне рішення рівняння має вигляд
X(x) = С1coslx +С2sinlx
Перша умова дає С1=0, друга умова приводить до трансцендентному
відносно власних значень рівнянню lcosll+hsinll=0, звідки 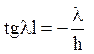 . Позначимо ll = m, hl = p,
і вирішимо рівняння
. Позначимо ll = m, hl = p,
і вирішимо рівняння 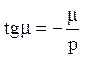 графічно:
графічно:
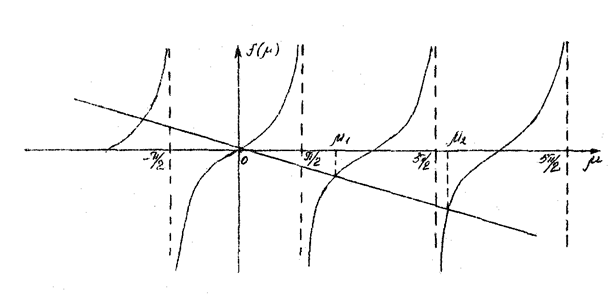
Хай m1 m2... mк.-
позитивні корені цього рівняння (негативні корені можна розглядати, відносячи
знак «-» до довільної постійної). Тоді 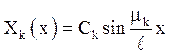 - власні функції задачі
- власні функції задачі
Для функцій Тk (t) маємо рівняння
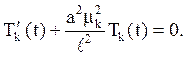
Звідки 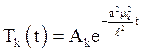 .
.
Будуємо ряд
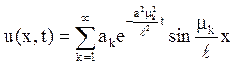
Тут ak = СkAk доберемо таку, щоб задовольнити початковій умові
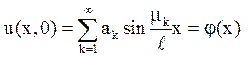
Зауважимо,
що функції 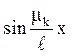 не є l - періодичними, тому останнє
рівняння не можна розглядати, як розкладання початкової функції j(х) в ряд Фур‘е по синусах на (0,l). Помножимо обидві
частини цього співвідношення на
не є l - періодичними, тому останнє
рівняння не можна розглядати, як розкладання початкової функції j(х) в ряд Фур‘е по синусах на (0,l). Помножимо обидві
частини цього співвідношення на 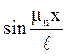 і проінтегруємо в межах від 0 до
l.
і проінтегруємо в межах від 0 до
l.
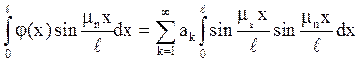
Оскільки власні функції ортогональні, то справа зберігається тільки складове, відповідне значенню k = n:
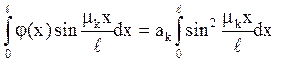 .
.
Підрахуємо інтеграл, що стоїть справа:
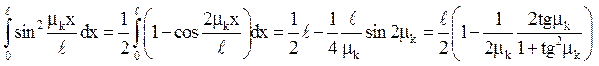
і пригадаємо, що 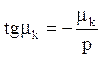 . Тоді
. Тоді
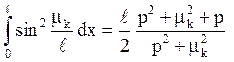
Знаходимо
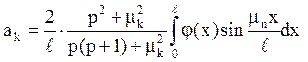 .
.
Залишилося знайдені значення аk підставити в ряд і записати відповідь.
Відповідь:
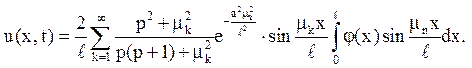
Приклад 3. Поставити
і вирішити крайову задачу про
визначення температури стрижня 0 ≤ х ≤ ![]() з
теплоізольованою бічною поверхнею, якщо його початкова температура є довільною
функцією х, а на кінці стрижня подається ззовні заданий тепловий потік.
з
теплоізольованою бічною поверхнею, якщо його початкова температура є довільною
функцією х, а на кінці стрижня подається ззовні заданий тепловий потік.
Постановка задачі. Хай на бічній поверхні стрижня відбувається конвективний обмін з навколишнім середовищем, температура якого є заданою функцією часу. Нехтуючи деформацією ізотермічних поверхонь, поставимо крайову задачу про визначення температури в стрижні коли на кінці стрижня подаються ззовні постійні теплові потоки.
Рівняння теплопровідності в даному випадку має вигляд:
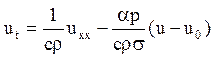 , (1)
, (1)
При 0 < t < + ¥, 0 < x < l, де р – периметр поперечного перетину стрижня; a - коефіцієнт теплообміну між поверхнею стрижня і навколишнім середовищем; температура якої рівна u0 (у нас - u1 = u0) с – питома теплоємність; l - коефіцієнт температуропровідності матеріалу, з якого виготовлений стрижень; r - густина маси; s - площа поперечного перетину.
U(x,l) = f (x) = - 4, 0 < x < l, - lsu x(0,t)= q1 (t) = 0
lsux(l,t) = q2(t), 0< t < + ¥
Хай, 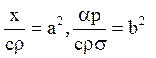 тоді
тоді
ut = a2uхx-b2u + b2u0; u0= 1; l = 1
u(x, 0)= f(x)= -4; ux(0,t)= ux(1,t)= 0.
Рішення даного рівняння шукатимемо у вигляді u = ![]() + w, де
+ w, де ![]() = v(x) рішення рівняння
= v(x) рішення рівняння
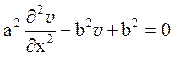 (2)
(2)
при ![]() x(0) =
x(0) = ![]() x(1)
= 0, aw – рішення рівняння
x(1)
= 0, aw – рішення рівняння
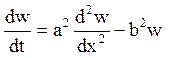 ,
(3)
,
(3)
за умов wx(0,t) = wx (0,1) = 0
w(x,0)= f(x) –
![]() (x) = - 4 –
(x) = - 4 –
![]() (x).
(x).
Дійсно, хай u
= ![]() + w, тоді
+ w, тоді
ut = ![]() t + wt = 0 + wt; uxx =
t + wt = 0 + wt; uxx = ![]() xx + wxx.
xx + wxx.
Складаючи (2) і (3), отримаємо
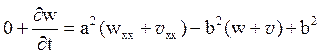
де ![]() .
.
Перевіримо ще початкові і крайові умови
u(x,0)= ![]() (x)+ w (x,0) =
(x)+ w (x,0) = ![]() (x)+f(x) –
(x)+f(x) – ![]() (x)=
f(x)
(x)=
f(x)
ux(x,t)|x=0 = ![]() ¢ (0)+wx(0,t)=0 ; ux(
¢ (0)+wx(0,t)=0 ; ux(![]() ,t)=
,t)= ![]() ¢(
¢(![]() )+wx(
)+wx(![]() ,t)
,t)![]()
Вирішуємо рівняння
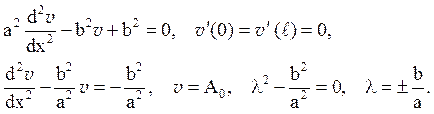
Підставляючи в рівняння, маємо:
0 –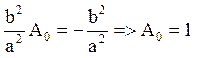
Вирішуємо відповідне однорідне рівняння другого порядку
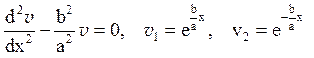
Загальне рішення однорідного рівняння:
![]() 00 = C1e
00 = C1e![]() ,
,
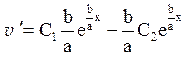 ,
,
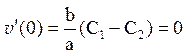 , (4)
, (4)
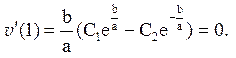 (5)
(5)
Отримаємо з (4) C1= C2 та з (5) – 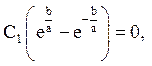 ,
звідки C1 = C2 = 0.
,
звідки C1 = C2 = 0.
Отже, рішенням рівняння (2) є функція
![]() (x) º 1.
(x) º 1.
Займемося тепер рішенням рівняння (3)
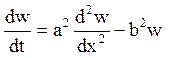 .
.
wx(0,t) = wx
(![]() ,t)= 0; w(x,0)
= -4 -1= -5.
,t)= 0; w(x,0)
= -4 -1= -5.
Рішення шукатимемо у вигляді
w(x,t)=X(x)T(t)
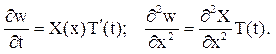
Підставляючи в (3), одержуємо
X(x)T¢(t) = a2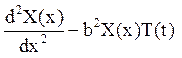 .
.
Розділимо обидві частини рівності на аХТ, отримаємо
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.