Существует ровно один многочлен, такой, что f(ΛA) = r(ΛA) и deg r < m, который определяется интерполяционными условиями:
Этот многочлен называется интерполяционный многочлен Лагранжа-Сильвестра. Тогда мы можем дать новое определение f(A).
Определение 7.2. Пусть функция f определена на спектре матрицы A, тогда f(A) = r(A), где r(λ) - интерполяционный многочлен Лагранжа-Cильвестра.
Свойства функции от матрицы:
1. Пусть λ1,…, λn- все собственные значения матрицы A ![]() Cn,n, тогда
f(λ1),…, f(λn)- собственные значения f(A).
Cn,n, тогда
f(λ1),…, f(λn)- собственные значения f(A).
2. Пусть матрицы A и B подобны, причем B= S-1AS, тогда f(B) = S-1f(A)S.
3. Если A = diag{A1, …, Ak}, то f(A) = diag{f(A1), …, f(Ak)}.
В пакете LinearAlgebra содержатся функции позволяющие вычислять различные функции от матриц. Рассмотрим эти функции.
Пример 7.1. Возвести
матрицу A в степени 2 и 0,5, где A = 
![]()
![]()

![]()

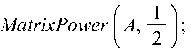
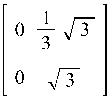
Пример 7.2. Найти
еA и еAx , где A = 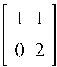
![]()
![]()
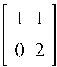
![]()
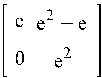
![]()
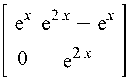
Пример 7.3. Найти A2,
cos(A) и еA, где A = 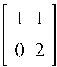
![]()
![]()
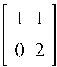
![]()

![]()
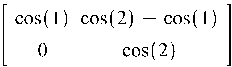
![]()
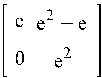
8.1 Уравнение вида AХ=ХB
Рассмотрим матричное уравнение AX= XB,
где ![]() ,
,![]() ,
,![]() .
.
Теорема 8.1. Общее
решение уравнения AX=
XB, где ![]() ,
, ![]() .
. ![]() ,
,![]()
![]() ,
,![]()
может
быть найдено по формуле: ![]() .
.
Где ![]() - общее
решение уравнения
- общее
решение уравнения ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Если ![]() , то
, то ![]() , если
, если ![]() ,
то
,
то ![]() - произвольная правильная верхняя треугольная
матрица.
- произвольная правильная верхняя треугольная
матрица.
Матрица X зависит от N
произвольных параметров 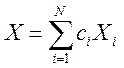 ,
,  , где
, где![]() ,
,
![]() ,
, ![]() .
.
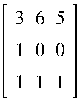
Пример 8.1. Решить матричное уравнение AX= XB,
где
A=
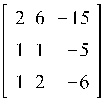 , B=
, B= 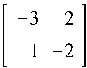
![]()
Ввод матрицы A:
![]()
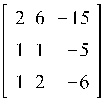
Ввод матрицы B:
![]()
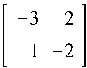
Найдем жорданову форму J1 матрицы A и преобразующую матрицу U:
![]()
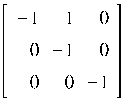
Найдем жорданову форму J2 матрицы B и преобразующую матрицу V:
![]()
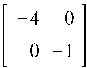
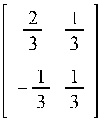
Найдем решение уравнения ![]() :
:
Вычисления выполняются вручную.
![]()
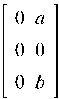
![]()
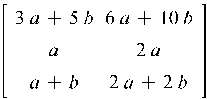
8.2 Уравнение вида AХ = ХA
Пусть дана матрица ![]() .
Будем решать следующую задачу: найти все матрицы
.
Будем решать следующую задачу: найти все матрицы ![]() ,
перестановочные с A. Для этого необходимо найти общее решение уравнения AX= XA. Так как уравнение AX= XA является частным случаем уравнения AX= XB,
то для его решения воспользуемся теоремой 8.1 и сформулируем новую теорему:
,
перестановочные с A. Для этого необходимо найти общее решение уравнения AX= XA. Так как уравнение AX= XA является частным случаем уравнения AX= XB,
то для его решения воспользуемся теоремой 8.1 и сформулируем новую теорему:
Теорема 8.2.
Общее решения уравнения AX=
XA, где ![]() ,
, ![]() ,
,![]()
может
быть найдено по формуле: ![]() ,
,
Где ![]() - общее
решение уравнения
- общее
решение уравнения ![]() ,
,![]() ,
, ![]() ,
, ![]() .
.
Если ![]() , то
, то ![]() , если
, если ![]() ,
то
,
то ![]() - произвольная правильная верхняя треугольная
матрица. Матрица X зависит
от N произвольных параметров
- произвольная правильная верхняя треугольная
матрица. Матрица X зависит
от N произвольных параметров 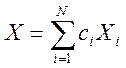 ,
,
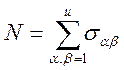 , где
, где![]() ,
,
![]() .
.
Пример 8.2.
Решить матричное уравнение AX=
XA, где A = 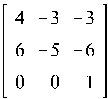
![]()
Ввод матрицы A:
![]()
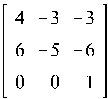
Найдем жорданову форму J1 матрицы A и преобразующую матрицу U:
![]()
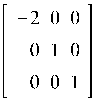
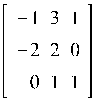
Найдем решение уравнения ![]() :
:
Вычисления выполняются вручную.
![]()

![]()
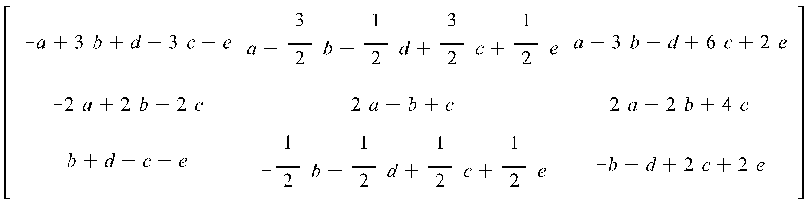
8.3 Решение уравнения AX – XB= C
Пусть дано уравнение AX – XB= C, где ![]() ,
,![]() ,
,![]() .
Это матричное уравнение эквивалентно системе m∙n
линейных уравнений относительно элементов
матрицы X.
.
Это матричное уравнение эквивалентно системе m∙n
линейных уравнений относительно элементов
матрицы X.
Рассмотрим соответствующее однородное уравнение AX – XB= 0. Если матрицы A и B не имеют одинаковых собственных значений, то уравнение AX – XB=0 имеет единственное решение; если же матрицы A и B имеют одинаковые собственные значения, то в зависимости от C возможны два варианта:
1. Уравнение не имеет решения.
2. ![]() , где
, где ![]() - произвольное частное решение
уравнения AX-XB=C,
- произвольное частное решение
уравнения AX-XB=C, ![]() - общее решение уравнения AX – XB=
C.
- общее решение уравнения AX – XB=
C.
Алгоритмизация данного типа уравнений отводится в качестве упражнения.
Нормы матриц
Определение 9.1. Неравенство A ≤ B между матрицами A = [ аij]и B =[ bij]одинаковых типов обозначает, что аij ≤bij . В этом смысле не всякие две матрицы сравнимы между собой.
Определение 9.2. Под абсолютной величиной (модулем)матрицы A= [ аij ] будем понимать матрицу |A| = [ | аij| ]
где |аij| — модули элементов матрицы A.
Если A и B— матрицы, для которых операции A + B и AB имеют смысл, то:
а) | A + B | ≤ | A | + | B |;
б) | A B | ≤ | A | · | B |;
в) | α A | = | α | · | A |;
(α — число).
Определение 9.3. Под нормой матрицы A = [ аij] понимается действительное число || A ||, удовлетворяющее условиям:
а) || A|| ≥ 0, причем ||A|| =0 тогда и только тогда, когда A = 0;
б) || α A || = | α | · || A || (α — число) и, в частности, || –A || = || A ||;
в) || A + B || ≤ || A || + || B ||;
г) || AB || ≤ || A || · || B ||;
(A и B — матрицы, для которых соответствующие операции имеют смысл).
В дальнейшем для матрицы A = [ аij]произвольного типа мы будем рассматривать главным образом три легко вычисляемые нормы;
1) || A
||m = 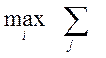 | аij | (т-норма);
| аij | (т-норма);
2) || A
||l = 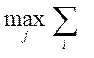 | аij | (l-норма);
| аij | (l-норма);
3) || A
||k = 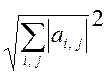 (k -норма).
(k -норма).
 Далее представлены алгоритмы для нахождения нормы
матрицы каждого вида:
Далее представлены алгоритмы для нахождения нормы
матрицы каждого вида:
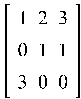
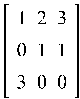
Пример 9.1. Найти m-норму для матрицы A, где A =
![]()
![]()

![]()
![]()
![]()
![]()
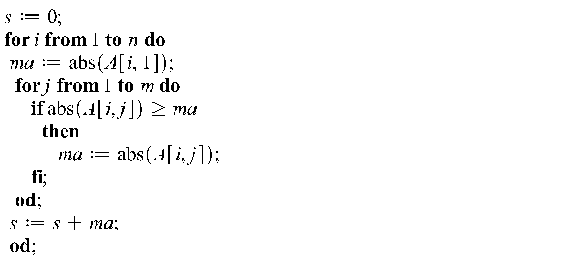
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 9.2. Найти l-норму для матрицы A, где A =
![]()
![]()

![]()
![]()
![]()
![]()
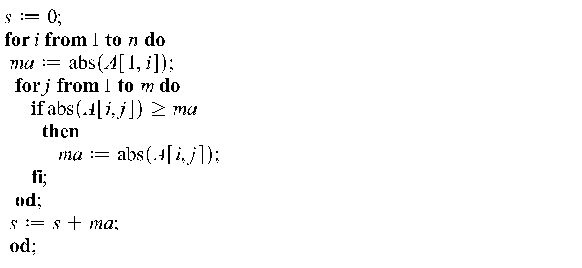
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
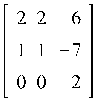
Пример 9.3. Найти k-норму для матрицы A, где A =
![]()
![]()
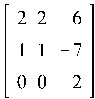
![]()
![]()
![]()
![]()
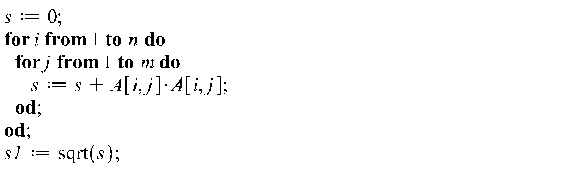
![]()
![]()
![]()
![]()
Генерация задач
Часто возникают проблемы с подготовкой контрольных и проверочных работ по данному курсу, что связано с недостатком имеющихся в учебных пособиях типовых заданий для индивидуальной работы группе студентов.
Используя Maple нетрудно решить эту проблему.
Возьмем, к примеру, наиболее легкий тип задач. Пусть у нас дана матрица A:
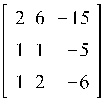
и необходимо найти собственные значения этой матрицы.
Решая поставленную задачу находим:
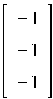
где этот столбец – вектор собственных значений, равных -1 кратности 3.
Необходимо растиражировать эту задачу, сохранив данные собственные значение и их кратность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.