Информатика и выч. техника \ Матричный анализ

Пакет аналитических вычислений Maple, страница 5

 


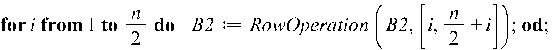
Второй вариант:


Глава 4

Матрица Мура-Пенроуза (псевдообратная)

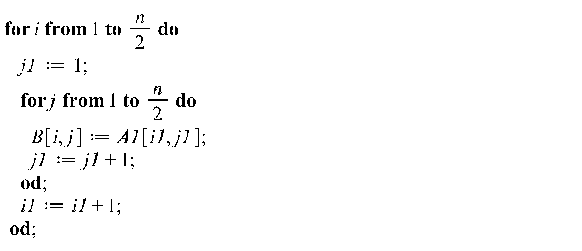
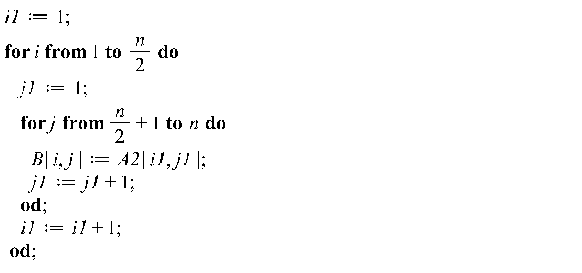
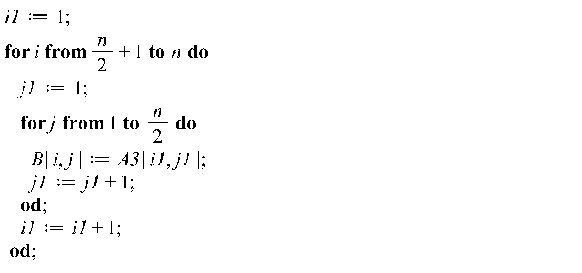
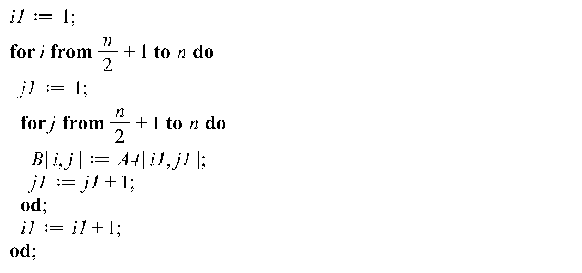
Теорема 4.1. (O скелетном разложении матрицы.) Пусть A  Pm,n,, rank A = r >0, тогда существуют B  Pm,r, CPr,n, такие, что A=BC и rank B = rank C = r.

Определение 4.1. Пусть A  Pm,n, тогда МП-матрицей или псевдообратной для матрицы A называется матрица A+ Pn,m такая, что выполняется следующее равенство:

1)  AA+A= A;

2)  A+AA+ =A+;

3)  (A+A)* =A+A;

4)  (AA+)* =AA+;

где A*=ĀT.

Теорема 4.2. Для любой матрицы APm,n существует единственная псевдообратная матрица A+.

Определение 4.2. Пусть имеется система m линейных уравнений с n неизвестными, которой соответствует матричное уравнение AX= B, где APm,n, X  Pn,1 , B  Pm,1. Столбец Y= B – AX называется невязкой столбца X. Если X - решение системы, то невязка равна нулю (Y= 0), если же  система несовместна, то столбец X, длина невязки которого минимальна, называется нормальным псевдорешением системы AX= B.

Теорема 4.3. Нормальное псевдорешение системы AX = B всегда существует, единственно и вычисляется по формуле X0 = A+B.

Нахождение МП-матрицы осуществляет специальная функция из пакета LinearAlgebra MatrixInverse, которая вычисляет обратную для любой матрицы, в том числе и для прямоугольной или вырожденной матрицы.

Пример 4.1. Найти псевдообратную матрицы A, если A=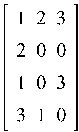

 


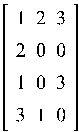
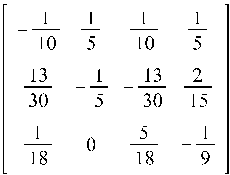
Можно найти МП-матрицу и алгоритмически, не применяя встроенной функции. Это помогает, когда необходимо произвести проверку в вычислениях того или иного шага в алгоритме.

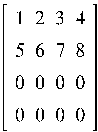
Пример 4.2.Найти псевдообратную матрицу матрицы A, если

A =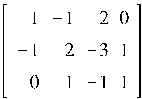

 


Ввод исходной матрицы и вычисление её скелетного разложения, и нахождение псевдо-обратной матрицы:

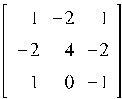
Следующий блок выполняет выделение из матрицы r первых линейно-независимых столбцов.

 

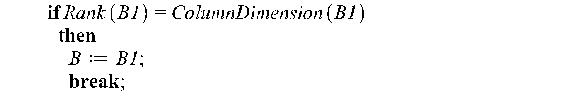
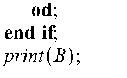
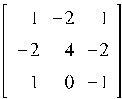
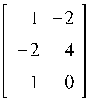
Находим матрицу C, A=BC:

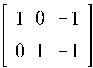
Получение МП-матрицы:

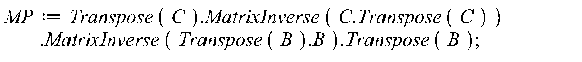
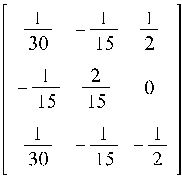
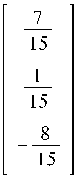
Вычисляем длину невязки:

Глава 5

Многочленные матрицы

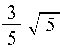
Определение 5.1. Множество V называется линейным или векторным пространством над полемP если:

а) любым элементам x, y из V поставлен в соответствие элемент z = x + y из V, называемый суммой x и y;

б)любому элементу x из V и любому числу λ из поля P поставлен в соответствие элемент λx, называемый произведением числа λ на элемент x так, что эти операции удовлетворяют следующим аксиомам:

1. 1) x + y = y + x

    2) (x + y) + z = x + (y + z)

    3) существует элемент 0 такой, что x+ 0 = x для любого элемента x из V

    4) для любого элемента x из V существует элемент –x из V такой, что x + (–x) = 0

2. 1) 1·x = x для любого элемента x из V

    2) α(βx) = (αβ)x для любых α, β из P и любого x из V

3. 1) (α + β)x= αx+ βx для любых α, β из P и любого x из V

    2) α(x + y) = αx+ αy для любого α из Р и любых элементов x, y  из V

Определение 5.2. Преобразование A, линейного пространства V, называется линейным, если:

1)  A(x+ y) = Ax+ Ay, для любого x и y из V;

2)  A(λx) =  λAx, для любого x из V и для любого λ из P, где P – некоторое поле.

Определение 5.3. Вектор x из V называется собственным для линейного преобразования F, если существует λ из P, такое что Fx= λx, число называется собственным значением линейного преобразования F соответствующего собственному значению x.

Пример 5.1. Найти собственные значения и собственные вектора для матрицы A, где A =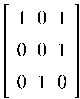

 


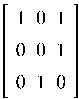
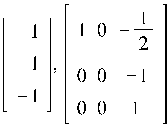
Определение 5.4. Многочлен |A– λ E| называется характеристическим многочленом матрицы A, а уравнение |A– λ E|=0 называется характеристическим уравнением. Корни характеристического уравнения называются  собственными значениями матрицы A.

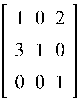
Пример 5.2. Найти характеристическую матрицу и характеристический многочлен матрицы A, где A =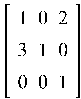

 


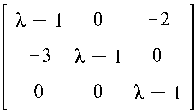
Определение 5.5. Скалярный многочлен  f(λ) называется аннулирующим  многочленом квадратной матрицы A, если f(A) = 0.

Аннулирующий многочлен ψ(λ) наименьшей степени со старшим коэффициентом, равным единице, называется минимальным многочленом матрицы A.

Пример 5.3. Найти минимальный многочлен матрицы A, где A =

 


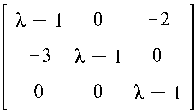
Определение 5.6.  Квадратная матрица порядка n, элементы которой – многочлены от переменной λ с коэффициентами из поля P называется многочленной матрицей или λ-матрицей.

Примерами многочленных матриц могут служить:

1)  Характеристическая матрица |A–λE|;

2)  Матрица с элементами из поля P.

Пример 5.4. Ввод характеристической матрицы A =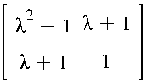  

 


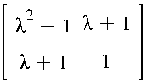
Определение 5.7. Элементарными преобразованиями матрицы A(λ) называются преобразования из следующих типов:

1)  умножение любой строки матрицы A(λ) на любой элемент  

2)  умножение любого столбца матрицы A(λ) на любой элемент  

3)  прибавление к любой i-ой строке матрицы A(λ) любой ее j-ой строки, умноженной на любой многочлен φ(λ) над полем P ().

4)  прибавление к любому i-ой столбцу матрицы A(λ) любого его j-ого столбца, умноженного на любой многочлен φ(λ) над полем P ().

В Maple элементарные преобразования выполняют функции ColumnOperation и RowOperationдля столбцов и строк соответственно.

Перестановка строк (столбцов)

Скачать файл