Динамические измерения. Проблемы динамических измерений. Входные сигналы и измеряемые величины. Погрешности динамических измерений, страница 17

Переходная характеристика имеет вид:

                           

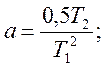
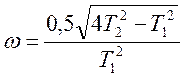
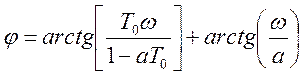
При произвольном выходном сигнале с нулевым начальным значением с учетом получаем:

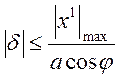
При монотонно-наростающем входном сигнале, скорость которого имеет не более одного внутреннего максимального:

,

Где - период собственных колебаний устройства.

Важным для практики классом входных сигналов является периодические сигналы, простейший из которых  синусоидальный сигнал. Он вызывает аналогичный отклик линейного СИ измерения в установленном режиме.

Представим частотные характеристики устройства в форме, соответствующей распространенному способу их нормирования

,

,

Тогда динамическая погрешность получается в виде:

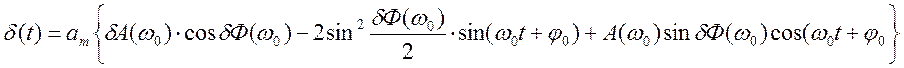
Отсюда получается, что для достаточно больших  то есть в установившемся режиме и для значительной части, в которой допустимо пренебрежение величины порядка малости выше 2-го:  получаем приближенную оценку.

Этот результат может быть использован и в случае, когда входящий сигнал представляет собой  сумму нескольких гармонических сигналов с частотой, не обязательно кратной минимальной.

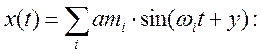
Для такого сигнала в установленном режиме справедливо следующая оценка погрешности:

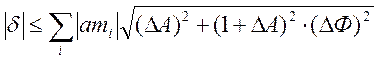
3.  Апостериорное оценивание.

Полученное в предыдущем 2-м случае оценки априорны – то есть при их получении не используют результат измерений. На основании результата измерений эти оценки можно улучшить. Для звеньев 1-го порядка имеем точное равенство:

то есть оценка погрешности измерения может быть определена с точностью до погрешности определяемой произведением выходящих сигналов по его зарегистрированному значению. Для звеньев 2-го порядка:

                                      

                                                                                           (25)

Точность этой оценки ограничена достигаемой точностью определения первых 2-х производных сигналов. Для звеньев 2-го порядка по результатам измерений можно оценить погрешность снизу следующим образом. Исходя из уравнения:

Получаем:                                                                               (26)

(26) полезно использовать , если

Для звеньев 1-го порядка максимальное значение погрешность достигает в точках перегиба у, а в точках максимального и минимального значений погрешность у = 0.

Коррекция динамики погрешностей измерения.

Скорректировать динамику погрешности означает (при отсутствии статических погрешностей) определить по выходному сигналу устройства у(t) входной сигнал x(t). Формально это обозначает решить уравнение:

                                                                                                               (27)

то есть фактически, найти В^-1. Рассмотрим условие корректности применительно к этому случаю. Выходящие сигнальные средства измерения являются откликом на входящий сигнал и поэтому решение существует. Это уравнение в формуле свертки 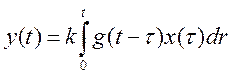 (11) теоретически решается однозначно. Однако импульсная характеристика реального устройства ограничена во времени, а полоса пропускания частоты конечна. Из этого следует наличие диапазона частот, в которых АЧХ=0. Поэтому решение уравнения (11) будет представлять собой любую сумму действительного входного сигнала k(t) и гармонических сигналов с частотами, при которых АЧХ=0. При этом непрерывная зависимой  решения от тех данных для уравнения (11) может отсутствовать. Пусть

,                                                                                                                (28)

А входящие сигналы.                                                                        (29)

тогда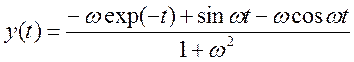

Если исходные данные содержат убывающую к 0 погрешность, то решение может содержать гармонические составляющие с неограниченно возрастающими частотами и неубывающими амплитудами. Таким образом, снижение погрешностей исходных данных при ограниченной полосе пропускания не гарантирует сходимости к истинному решению. Если заранее известно, что спектр  сигнала x(t) находится внутри полосы пропускания СИТ, то проблема вообще не однозначности в связи с корреляцией динамических погрешностей вообще не возникает.

Т.о. однозначность решения обратной задачи  существенно связана с объемом априорной информации при измерениях. Априорная информация всегда достаточна для проблемы неоднозначности,  иначе задача измерения не может быть поставлена.

Т.о. расположение спектра выходного сигнала внутри полосы пропускания частот (рабочей полосы частот) есть по существу условие правильного применения устройства.

Общая постановка задачи коррекции такова: требуется решить уравнение , если известны оценки оператора В, выходного сигнала y(t) и норма их погрешностей . Решение понимается как нахождение оценки входного сигнала х и нормы его погрешностей . Погрешность либо погрешность нахождения оператора конкретного экземпляра устройства, либо допускаемое отклонение конкретного оператора от нормируемого для устройства данного типа.  Погрешность  есть погрешность определения y(t) \, которая в общем случае состоит из погрешностей регистрации и отсчитывания. Погрешность есть погрешность коррекции, т.е. по существу погрешность определения динамической погрешности . Очевидно, что коррекция целесообразна лишь в том случае, когда <.

1.  Комплексная область.

Пусть в уравнении динамики (10)

Y(p)=KW(p)X(p)

Динамические свойства СИ представлены передаточной функцией W(p), существенно также преобразование Лапласа выходного сигнала Y(p). Тогда преобразование Лапласа для входного сигнала:

Чаще всего передаточная функция представляется в аналитической форме. Выходной сигнал y(t), как правило, представлен в виде некоторой кривой записи во временной области. Преобразовать y(t) в комплексную область можно аппроксимируя его аналитическим выражением на основе полученных при отсчитывании значений полученных значений и переходя к выражению Y(p) с помощью таблицы преобразования Лапласа. Можно также от совокупности отсчитываемых значений Y(t) перейти к дискретному представлении его в комплексной области на основе Z-преобразования и далее продолжать оперировать с дискретными представлениями и в результате прийти к дискретному представлению X(t) либо переходить к непрерывному представлению X(p), и, следовательно, X(t), используя известные соотношения между непрерывным и дискретным преобразованием Лапласа.