Силовой анализ механизма грохота

4. СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА ГРОХОТА

4.1 Определение сил, действующих на механизм

4.1.1. Определение сил инерции

При движении звена различные его точки в общем случае имеют различные ускорения. По принципу Даламбера к каждой точке звена, обладающей элементарной массой dm, следует приложить элементарную силу инерции , где  – ускорение массы dm. Так как звено имеет множество точек, то и сил инерции, действующих на звено, - множество. На практике при расчете самого звена на прочность ограничиваются конечным числом сил инерции, которые сосредоточивают в центрах тяжести. В дальнейшем обычно эти силы приводят к центру масс S звена. В результате на центр масс звена действует результирующая сила инерции (главный вектор инерции), называемая силой инерции , и главный момент сил инерции звена (момент пары сил инерции) .Сила инерции  и момент пары сил инерции . Определяются по формулам соответственно:

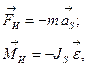
где: т – масса звена;  – вектор ускорения масс;  – момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения;  – угловое ускорение звена. Знак минус показывает, что сила и момент и инерции направлены противоположно ускорению.

Находим для исследуемого станка угловые ускорения звеньев и линейные ускорения центров масс звеньев в проекциях на оси координат.

Для начального звена в третьем положении соответственно будем иметь:

    

Для остальных звеньев ускорения центров масс и угловые ускорения находим по формулам, связывающим их с аналогами скоростей и ускорений [2, 3], которые имеют следующий вид:

,           

.              (4.1)

Результаты расчета ускорений звеньев по формулам (4.1) приведены в таблице 4.1.

Таблица 4.1. Ускорение центров масс и угловые ускорения звеньев

Определив ускорения звеньев, находим величины моментов и сил инерции звеньев механизма:

- для звена 1  

- для звена 3  

- для звена 4  

- для звена 5  

4.2. Определение уравновешивающего момента и реакций

в кинематических парах аналитическим методом

5.2.1. Силовой анализ структурной группы 4 – 5

Прикладываем к структурной группе все действующие на нее силы (рис. 4.1). Действие на звено 5 со стороны стойки 0 заменяем реакцией , а на звено 4 со стороны звена 3 – реакцией  в проекциях на оси. Также в точке D прикладываем в проекциях на оси внутреннюю реакцию .

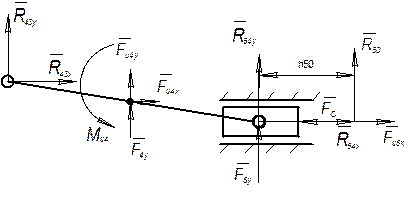
Рис. 4.1. Силовой анализ группы 4 – 5

Записываем в проекциях на оси координат условие равновесия сил, действующих на звено 5:

откуда

 находим из условия равновесия 4 звена:

Составим сумму моментов для 4 звена относительно точки C:

;

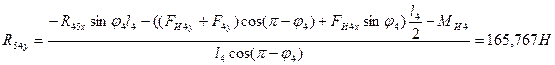Уравнение равновесия для звена 4 по оси y:

Записываем условие равновесия сил в проекциях на ось y для 5 звена

откуда

Находим сумму моментов относительно точки D для звена 5:

откуда

.

4.2.2. Силовой анализ структурной группы 2 – 3

Помимо заданных сил на группу действуют реакции ,  и  (рис. 4.2).

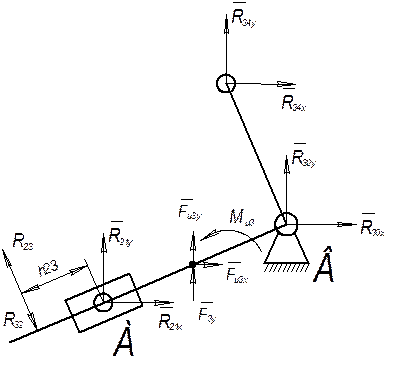
Рис. 4.2. Силовой анализ группы 2 – 3

Силы представлены через их проекции на оси координат. Проекции  и  найдены из анализа предыдущей группы:

, .

Для определения реакции  составим сумму моментов относительно точки B:

;

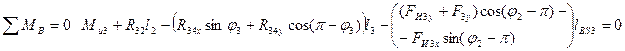
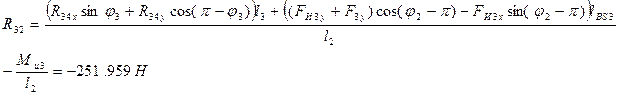Реакцию  найдем из условий равновесия сил, действующих на звено 3 в проекциях на оси:

.

Реакцию  найдем из условий равновесия сил, действующих на звено 2 в проекциях на оси:

4.2.3 Определение уравновешивающего момента и реакции в кинематической паре 0 - 1

Составляем уравнения равновесия начального звена механизма (рис. 4.3):

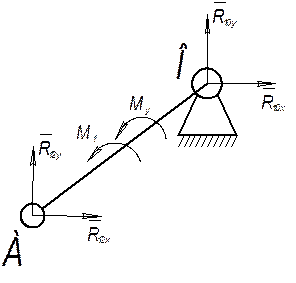
Рис. 4.3. Силовой анализ начального звена

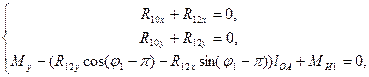             (4.2)

где:, , ,  – проекции на оси координат реакции на звено 1 стойки 0;  – уравновешивающий момент.

Решая (4.2), найдем:

4.3. Определение уравновешивающего момента и реакций

в кинематических парах графическим методом

4.3.1 Силовой анализ структурной группы 4 – 5

Рисуем структурную группу 4 – 5 и прикладываем к ней все действующие силы и моменты. Реакцию  изображаем разложенной на нормальную  и касательную