





Глава 3. Алгебраические линии и поверхности второго порядка.
§3.1. Алгебраические линии второго порядка.
Плоская линия L, заданная уравнением Ф(x,y)=0, называется алгебраической, если функция Ф(x,y) представляется конечным слагаемых вида :
αkL *xk*yL ,где k и L –целые неотрицательные числа, αkL - константы.
Наибольшее значение суммы (k+L) называется порядком алгебраической линии.
Линии, не являющиеся алгебраическими, называют трансцендентными.
Пример 1:
x2+y2-1=0 – алгебраическая линия второго порядка(окружность единичного радиуса с центром в начале координат).
Пример 2:
y – x + x3/3! - x5/5! + x7/7! - … =0 трансцендентная линия(бесконечный ряд).
В соответствии с определением, общие уравнения первого и второго порядков имеют вид:
линии 1-го порядка:
α1,0Ax + α0,1By + α0,0C , (1)
A и B не равны нулю.
Это прямые линии.
линии 2-го порядка:
Ax2 + Bx2y + Cy2 + Dx + Ey + F = 0, (2)
A,B,C не равны нулю одновременно.
Пусть коэффециенты A,B,….,F в уравнениях (1) и (2) имеют некоторые значения, такие, что в выбранной системе координат OXY эти уравнения определяют некоторые конкретные линии.
Если выбрать другую систему координат, то уравнения для этих линий станут другими.
При этом существенные обстоятельства:
1) в новой системе линии по прежнему будут алгебраическими, причем порядок её сохранится;
2) можно так подобрать новую систему координат, что уравнения данной линии примут простейший(канонический) вид. Эта система называется канонической для данной линии .
Очевидно, что прямая , заданная уравнением (1), в своей канонической системе будет иметь простейшее уравнение x/=0 или y/=0:
OXY : Ax + By + C = 0
O/X/Y/: y/=0
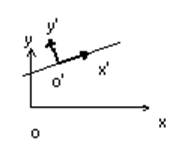
Несколько сложнее с уравнением (2) :
В зависимости от соотношений между коэффециентами A,B,…,F ,уравнение (2) можно привести к одному из простейших видов(в соответствующей канонической системе координат O/X/Y/):
1) x// a2 + y// b2 = 1 (эллипс)
2) x// a2 – y// b2 = 1 (гипербола)
3) y/2 = 2px/ (парабола)
4) a2x/2 – b2y/2 = 0 (две прямые, пересекающиеся в начале координат)
5) y/2 – a2 = 0 (две параллельные прямые)
6) y/2 = 0 (одна прямая)
7) a2x/2 + b2y/2 = -1 (круг радиуса ноль,т.е. точка)
8) x/2 / a/2 + y/2 / b2 (этим двум уравнениям 8 и 9 не )
9) y/2 + a2 = 0 ( удовлетворяет ни одна точка )
Эллипс:
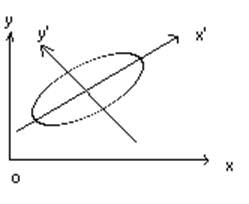
В OXY : Ax2 + Bxy + Cy2 + …= 0
В O/X/Y/ : x/2 / a2 + y/2 / b2 = 1 (система каноническая)
Замечание :
Подобрать для заданного уравнения каноническую систему координат не просто.
Линиями 1) – 9) исчерпываются все кривые, определяемые уравнением (2).
Таким образом осталось исследовать форму и свойства эллипса,гиперболы и параболы, заданных своими каноническими уравнениями.
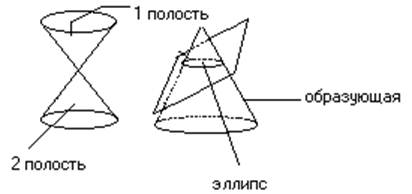
Эти линии можно рассматривать ещё и как канонические сечения.
Эллипс : плоскость пересекает образующие только одной полости конуса.
Гипербола: плоскость пересекает образующие обеих полостей конуса.
Парабола: плоскость параллельна одной из образующих конуса.
Движение частицы в гравитационном поле точечного тела происходит по одному из конических сечений.
ЭЛЛИПС.
Каноническое уравнение x2 / a2 + y2 / b2 = 1 (1)
a>0, b>0 (2). Будем всегда считать, что a ³ b т.к. в другом случае всегда можно выбрать другую систему координат, сделав замену x наy и y на x.
Числа a и b называют соответственно большой и малой полуосью эллипса.
При a = b получим окружность.
Обозначим C º(a2 - b2)½ (т.е. корень из разности квадратов)
Можно показать, что эллипс определяемый уравнением (1) – есть множество точек, для которых сумма расстояний r1 и r2 до двух фиксированных точек F1(-C,0) и F2(C,0),
называемых фокусами, есть величина постоянная и равна 2a :
r1 + r2 =2a
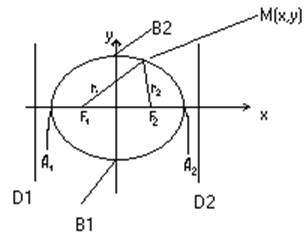
A1(-a,0) ; A2(a,0)
B1(0,-b) ; B2(0, b)
F1(-C,0) ; F2(C,0)
x2 / a2 + y2 / b2 = 1
r1+r2 = 2a
a ≥ b
D1 и D2 – директрисы
С = (a2 – b2)½ (т.е. квадратный корень из разности квадратов а и b)
Можно доказать, что при любом положении точки М:
{ r1 = a + ex ;
{ r2 = a – ex . (5)
где e = C/a = (1 - b2 / a2 )½ < 1 (6) - эсцентриситет эллипса.
Эта величина характеризует степень вытянутости эллипса.
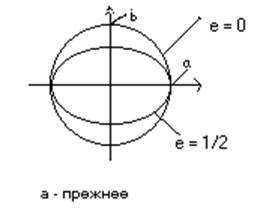
Директрисы эллипса – это две прямые, определяемые уравнениями :
1) x = - a/e (отвечает фокусу F1)
2) x = + a/e (отвечает фокусу F2)
Расстояние от М до D1 есть d1, расстояние от М до D2 есть d2.
Пусть r1 иd1 расстояния произвольной точки эллипса N соответственно до фокуса F1 и отвечающей ему директрисы D1 , аналогично r2 и d2.
Тогда справедливо равенство:
r1 / d1 = r2 / d2 = const = e
Из рисунка ясно, что при любом x : d1 = a / e + x ; d2 = a / e – x
Добавим (5) и получим (8)
Оптическое свойство эллипса.
α = β - свойство эллипса.
n – нормаль.
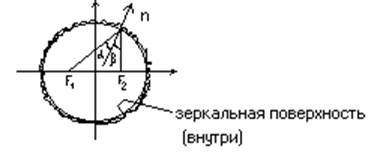
Все лучи, выходящие из F1, собирутся в F2.
§3.3 ГИПЕРБОЛА.
Каноническое уравнение гиперболы : x2 / a2 - y2 / b2 = 1 (1)
Гипербола задаётся парой чисел, называемых действительной и мнимой полуосями гиперболы.
C = (a2 + b2)½ ; a>0, b>0. (2)
Можно доказать, что гипербола есть множество точек, для которых абсолютна величина разности расстояния r1 и r2 до двух фиксированных точек F1 (-C,0) и F2(C,0), называемых фокусами, есть величина const = 2a .
| r1 – r2 | = 2a (3) – уравнение гиперболы, эквивалентно (1).
Рис
Эксцентриситет гиперболы: e (x = ± a / e)
Можно сказать, что
r1 = { a + ex; x>0
{ a – ex; x<0 (4)
r2 = { a + ex; x>0
{ a - ex; x<0
(х – координата точки М)
e = C / a = (1 + a2 / b2)½ (5)
Свойства гиперболы:
1) если r1 и d1 - расстояния произвольной точки M(x,y) до F1 и до отвечающей этому фокусу d1, а числа r2 и d2 – аналогично, то r1 / d1 = r2 / d2 = const = e (6)
Доказательство: пусть x>0, то из рисунка видно, что d1 = x + a / e ; d2 = x – a / e.
Отсюда следует, условие (6)
2) оптическое свойство:
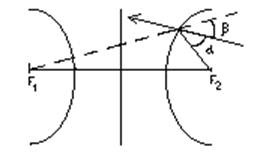
α = β
Все лучи, выходящие из F1 , после отражения кажутся исходящими из F2.
§3.4. ПАРАБОЛА.
Каноническое уравнение параболы: y = 2px (1)
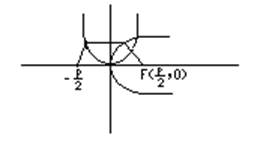
Парабола задаётся параметром p>0.
Легко доказать, что парабола ( из (1) ) есть геометрическое место точек, для которых расстояние r до фокуса равно расстоянию до директрисы d, заданной уравнением x = p/2.
r = d (2) - уравнение параболы, эквивалентно (1)
Если r и d - расстояния точки эллипса (гиперболы) до фокуса и до отвечающей этому фокусу директрисы, то отношение r / d = e (эллипса(гиперболы)), то по аналогии:
e = r / d = 1 (параболы).
Оптическое свойство параболы:
α = β
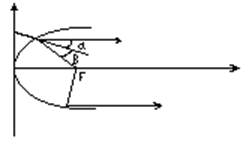
Лучи, выходящие из фокуса, после отражения идут параллельно оси параболы. Это свойство широко применяется в технике.
§3.5. АЛГЕБРАИЧЕСКИЕ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА.
Поверхность S , заданная уравнением f(x,y,z) = 0 , называется алгебраической, если f(x,y,z) представляется конечным числом слагаемых вида α klmxkylzm, где k,l,m –целые неотрицательные числа, а αklm – некоторая const.
Наибольшее значение суммы k+l+m называется порядком алгебраической суммы или алгебраическим порядком.
В соответствии с этим определением, общие уравнения поверхностей первого и второго порядков имеют вид:
1-й порядок
αx/y0z0 + αx0y/z0 + αx0y0z/ + αx0y0z0 из этого следует:
Ax + By + Cz + D = 0
A, B, C = 0 одновременно.
2-й порядок
Ax2 + By² + Cz² + Dxy + Eyz + Mzx + Gx + Hy + Kz+L= 0
Здесь первые шесть коэффециентов не равны нулю одновременно.
Для любой поверхности S, заданной в некоторой системе координат (O,X,Y,Z) уравнением вида Z можно так подобрать новую систему координат (O/X/Y/Z/),
что уравнение этой поверхности примет простейший(канонический) вид. При этом порядок поверхности сохраняется.Такую систему координат называют канонической для данной поверхности.
Важнейшие поверхности 2-го порядка:
1)эллиптический цилиндр:
x² / a² + y² / b² = 1
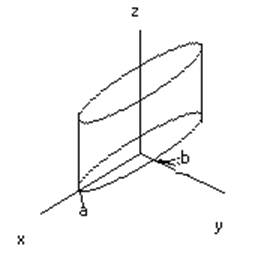
Замечание:
Гиперболический цилиндр x²/a² + y²/b² = 1
Параболический цилиндр y² = 2px
2)эллипсоид
x² / a² + y² / b² + z² / c² = 1
a,b,c – полуоси эллипсоида .
Сечение эллипсоида плоскостью z = h (h ≤ c):
x² / a² + y² / b² = 1 – h² / c²
Обозначим a* = a(1 – h² / c²)½
b*= b(1 – h² / c²)½
отсюда следует x² / (a*)² + y² / (b*)² = 1 (эллипс с полуосями)
карта эллипсоида(сечения поверхности плоскостями z = const = h)
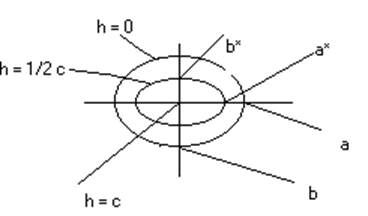
Карты :
x = const
y = const
z = const
Если a = c то такая поверхность называется эллипсоидом вращения .
Можно доказать, что линии пересечения этого эллипсоида с любыми плоскостями представляют собой эллипсы.
3)Однополостный гиперболоид
x² / a² + y² / b² - z² / c² = 1
Карты: сечение любой плоскостью z = const даёт эллипс
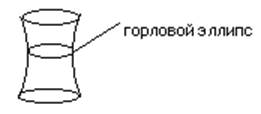
(x - const) сечение через A,B,C – гипербола с уравнением x² / y² - z² = 1.
Cвойство:
наличие прямолинейных образующих . Это линии, всеми своими точками лежащие на поверхности.
Можно доказать, что через каждую точку поверхности однополостного гиперболоида проходят две прямолинейные образующие.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.