Другие предметы \ Теория автоматического управления

Автоматизация. Автоматические и автоматизированные САУ. Классификация систем, страница 4

- постоянная времени характеризует величину сопротивления перемещению звена, численно равна времени равномерного перемещения звена от исходного предельного до равномерного положения с такой скоростью, при которой сила сопротивления достигнет максимального значения восстанавливающей силы. и всегда больше 0, может равняться 0 при отсутствии вязкого трения.

Рассмотрим установившееся положение звена.

; (8)

;

- коэффициент передачи, который характеризует, во сколько и насколько изменяется выходной сигнал звена при воздействии данного входного.

- коэффициент статистики

Перепишем уравнение (7)

(9)

Решение уравнения (9) получается в виде суммы общих и частных решений.

(10)

Выражение (10) характеризует свободное выражение звена, т.е. его поведение при отсутствии внешних воздействий.

(11)

и - постоянная интегрирования

и - корни характеристического уравнения

(12)

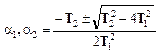
Передаточная функция в операторной форме

(1)

Уравнение (1) связывает выходную величину с входной с учетом производных на стержне второго порядка. В общем случае для систем уравнения: 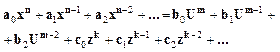(2)

В выражении (2) U и z – это внешнее воздействие на систему. Для САУ справедлив принцип суперпозиции, согласно которому реакция системы на сумму внешних воздействий равна реакции системы. На каждое воздействие в отдельности.

Поэтому изучать САУ можно по уравнению: (3) или

(4)

Введем, оператор дифференцирования: , и т.д., получаем

(5)

(6)

- собственный оператор управляемой величины

- собственный оператор входного воздействия

Т.е. получим, что передаточная функция показывает как входная величина звена преобразуется во выходную.

Преобразование входной величины в выходную характеризуется также статич. коэф. , однако он хар-ет преобразование в статич. режиме, когда выполняется 2 условия

, т.е. в статическом режиме .

Линеаризация

Пусть функция непрерывна в окрестностях конкретной точки и имеет все производные. Тогда эта функция может быть разложена в ряд Тейлора.

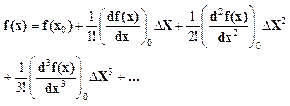(1)

Если задана функция двух переменных и она определена в окрестностях двух точек, то она также может быть разложена в ряд Тейлора.

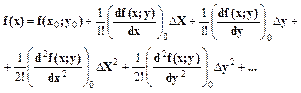(2)

Если выполняется условия (1) и (2) значит статическая характеристика может быть линеаризована. При линеаризации рассматриваются только малые отклонения для заданной точки .

Т.о. отклонение в степени становится пренебрежительно мало. Запишем выражение функции в окрестностях точки , 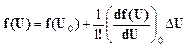(3)

Перейдём в выражении (3) к величинам входных и выходных сигналов ,

, (4) – линейное

Т.о. линеаризация заключается в замене нелинейной статич. характеристике линейной зависимостью в окрестностях некоторой точки . При динамич. процессе поведения СУ в общем случае описывается выражением.

(5).

Выражение (5) – функция нескольких переменных. В общем случае выражение (5) может быть сложным и нелинейным. Пусть функция непрерывна и определена в окрестностях заданной точки.

Разложим её в ряд Тейлора.

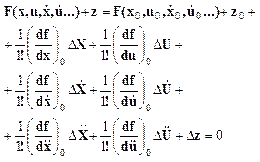(6)

Введём обозначение

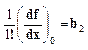
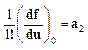
С учетом этих обозначений:

Учитывая выражение (5) перепишем выражение (7) в систему уравнений

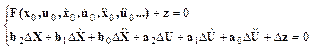(8)

Система уравнений (8) содержит только линейные операции, т.е. выполнена линеаризация исходного выражения (5). Система (8) справедлива только в окрестностях выбранной области переменной линиаризированное уравнение становиться неточным.

Тепловые динамические звенья автоматики

-Двигатели

-Датчики

-усилители

Практически для всех устройств, диф. уравнения которых имеют порядок не выше 2, можно записать.

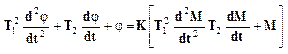(1)

В этом уравнении производная в левой части характеризует те обстоятельства, что на входное воздействие, но и на скорость его изменения и ускорения устройство любой природы, принципа действия и устройства описывающееся диф. уравнением ??? вида,

полученного на основе уравнения (1), и называется динамическим звеном.

Безинерционное или усилительное звено

В этом звене выходная величина в каждый момент времени пропорциональна входной величине.

(2)

- изображение

(3)

Инерционное звено

Звено, у которого при приложении какого-либо воздействия, реакция не сразу достигает конечного значения, а возрастает постепенно, в большинстве случаев по экспоненте.

Апериодическое звено первого порядка

(4)

(5)

Инерционное звено второго порядка

(7)

Интегрирующее звено

В нем в установившемся режиме линейная зависимость связывает входную величину и производную выходной величины, т.е. выходная величина пропорциональна по времени интегралу входной величины.

(8); ;

; (9) – передаточная функция

Дифференцирующее звено

К дифиринцирующим звеньям относят звенья в которых в установившемся режиме выходная величина пропорциональна производной по времени входной величине, т.е. чем больше скорость изменения входного сигнала, тем больше величина выходного.

(12);

- идеальное диф. звено

(14)

(15) – реальное звено

Формирующее звено – звено, в котором выходной сигнал определяется двумя слагаемыми, одним из них является входной сигнал, другим является сигнал пропорциональный производной этого сигнала.

(17)

Примечание: передаточная функция формирующего звена является приблизительной передаточной обратной функцией инерционного звена, поэтому если применить формирующее звено совместно с инерционным, то при равенстве их постоянных времени влияние инерционного звена устраняется и система становиться безинерционной. Это свойство используется для улучшения качества работы систем.

Колебательное звено

(18)