Автоматизация технологических процессов и производств, страница 2

Требуемое время регулирования: t_р = 22 с;

Допустимое отклонение параметра от установившегося значения φ = 8;

Величина внешнего возмущающего воздействия λ = 0.3;

Построим кривую разгона, в программе MathCAD, по данным

из Таблицы 1.

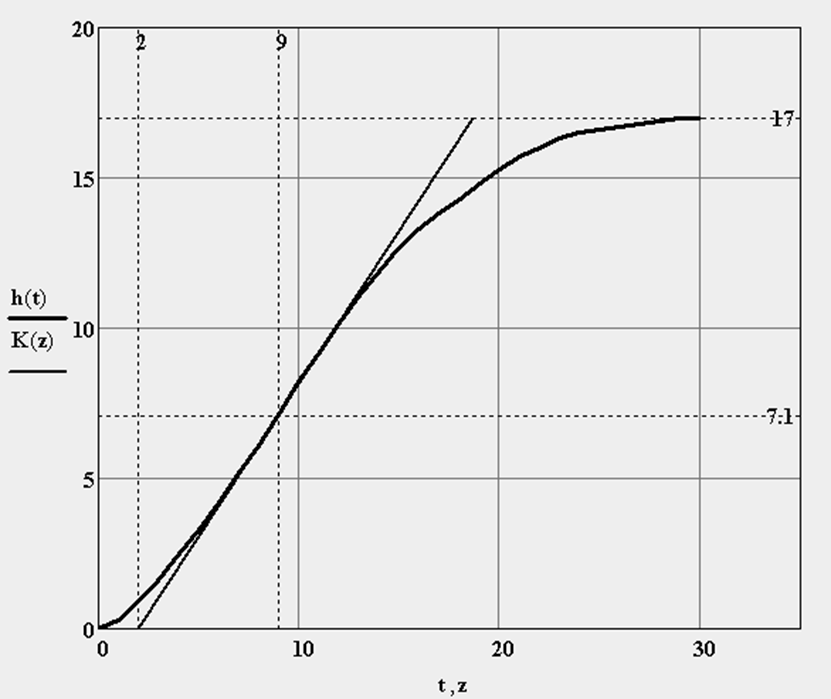
Заданная кривая разгона.

Передаточная функция апериодического звена 2 порядка имеет вид:

         

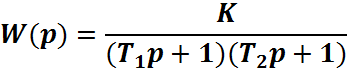
Для нахождения значений параметров Т₁ и Т₂ составим систему уравнений:

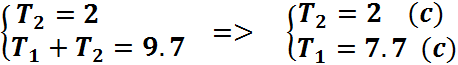
 Коэффициент усиления К = 17.

Таким образом, получили передаточную функцию разомкнутой системы:

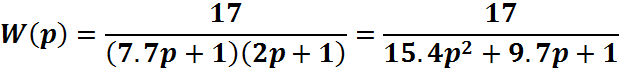
Построим кривую разгона по полученной передаточной функции.

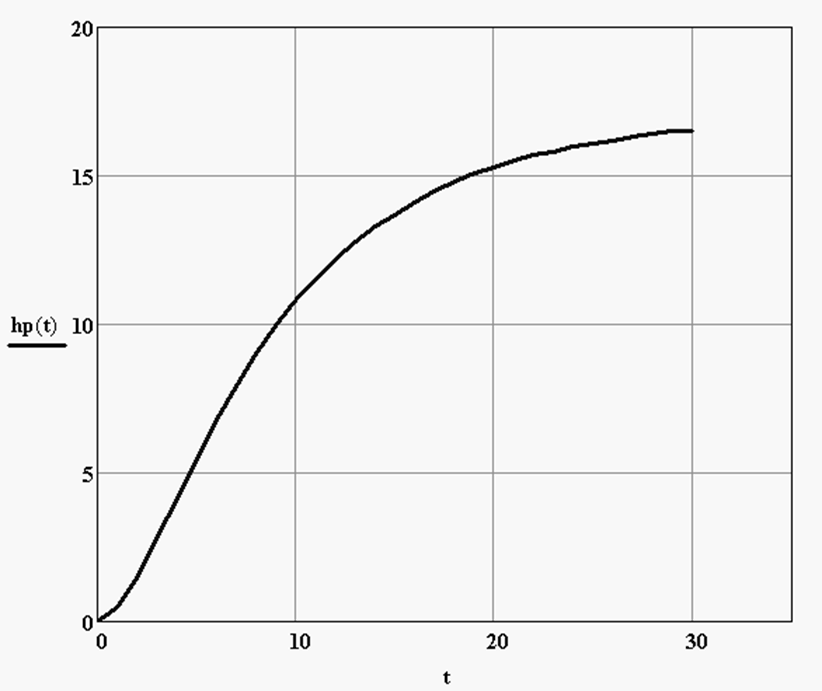
Рассчитаем среднеквадратичное отклонение полученной кривой разгона   от заданной:

         

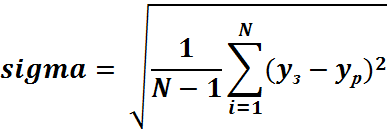
где     у_з – заданное значение выходной координаты;

          у_р – рассчитанное значение выходной координаты;

          N – число экспериментальных точек.

Значение sigma не должно превышать 10.

Таблица 2.

t	0	1	2	3	4	5	6	7	8	9
h(t)	0	0.3	0.9	1.6	2.5	3.3	4.2	5.2	6.1	7.1
hр(t)	0	0.459	1.48	2.78	4.15	5.49	6.77	7.93	8.99	9.93
t	10	11	12	13	14	15	16	17	18	19
h(t)	8.2	9.2	10.2	11.1	11.9	12.7	13.3	13.8	14.3	14.8
hр(t)	10.8	11.5	12.2	12.8	13.3	13.7	14.1	14.5	14.8	15.1
t	20	21	22	23	24	25	26	27	28	29	30
h(t)	15.3	15.7	16.0	16.3	16.5	16.6	16.7	16.8	16.9	17.0	17.0
hр(t)	15.3	15.5	15.7	15.8	16	16.1	16.2	16.3	16.4	16.5	16.5

Проведя расчёты получаем:

Т.к. sigma меньше 10, значит, кривую разгона можно выразить полученной нами передаточной функцией разомкнутой системы:

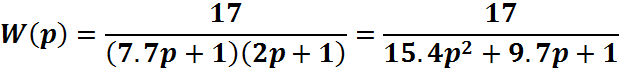
Структурная схема представленной САУ изображена на рисунке,

где    

W₁ – устройство управления: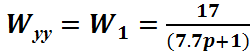             

W₂ – объект управления: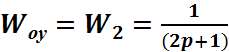                    

 

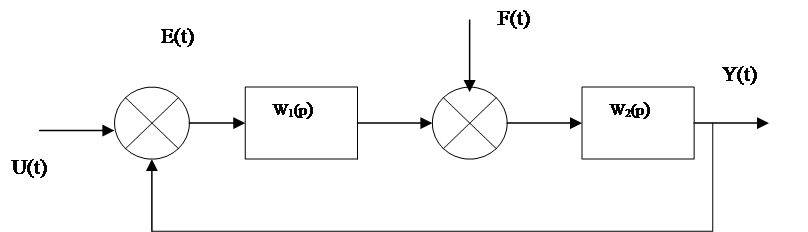Рисунок - Структурная схема исходной САУ

3. Анализ качества исходной САУ

1.  Главная передаточная функция замкнутой системы:

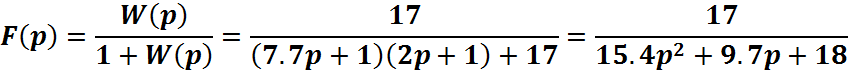
2.  Передаточная функция по возмущению:

 

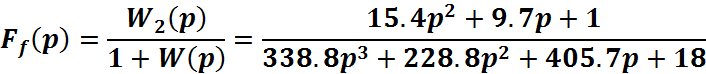
Анализ качества системы автоматического управления принято оценивать  с помощью следующих  показателей – времени регулирования, величины перерегулирования, значения ошибки в установившемся режиме, точности, и числа колебаний регулируемой величины за время переходного процесса.

Интервал времени, по истечении которого отклонение переходной характеристики от установившегося значения не превышает величины  d = 5%, называется временем регулирования t_p. Время регулирования является основной характеристикой быстродействия системы, т.е. определяет длительность пере­ходного процесса. Примем d = 5%.

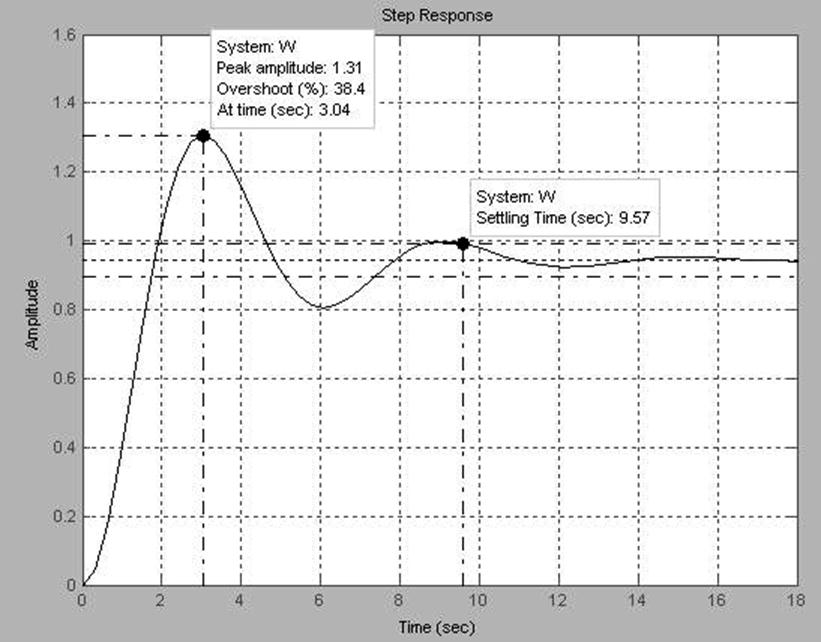
График главной передаточной функции исходной САУ

  Анализируя главную передаточную функцию замкнутой системы F(p), с помощью программного пакета MATLAB, получили следующие характеристики:

Время регулирования:    t_p = 9.57 (c)           

Величина перерегулирования: σ = 38.4 %  

Расчитаем желаемы характеристики:

K_ж = K/λ=17/0.3 = 57

σ_ж = φ*100/Kж = 8*100/57=14 %

Определим запасы по фазе и амплитуде исходной САУ, используя графики логарифмических частотных характеристик.

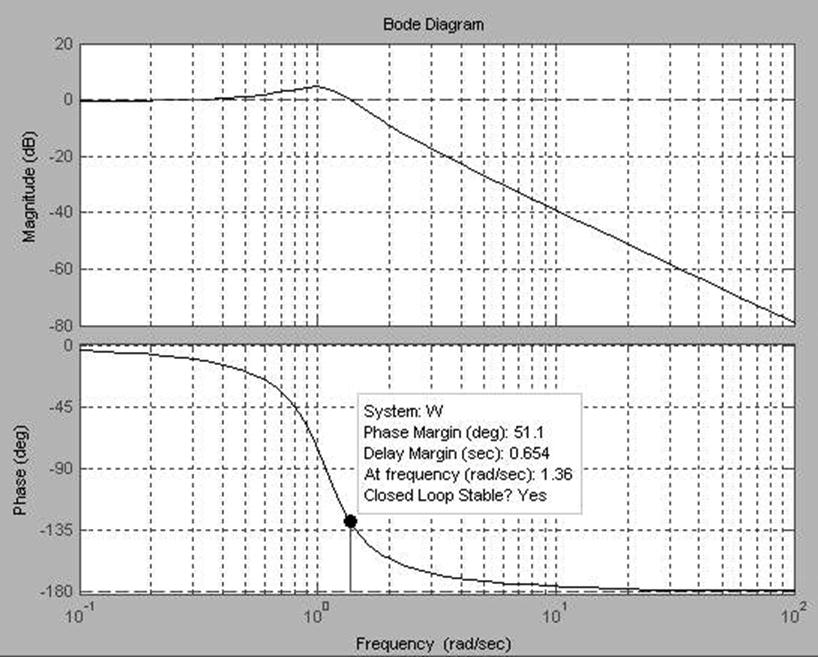
ЛФЧХ и ЛАЧХ главной передаточной функции исходной САУ

Для устойчивости замкнутой системы, точка пересечения фазовой характеристики с линией -180⁰ должна лежать правее частоты среза, то есть правее точки пересечения амплитудной характеристики с осью абсцисс.

Требования по запасу устойчивости  DL(w) = 16 - 20 дБ, Dj(w) > 40⁰.

Запас по фазе: Δφ(ω)= 51.1⁰;

Запас по амплитуде:    ΔL(ω) обеспечен.

Построим график передаточной функции по возмущению:

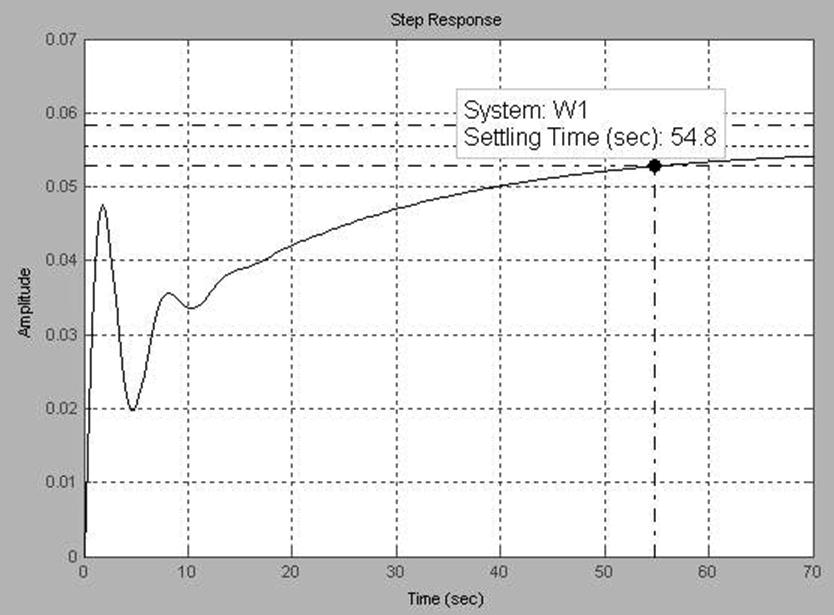
Кривая переходного процесса по возмущению

Время регулирования: t_р = 54.8 с

Таблица 3 - показатели исходной и желаемой САУ.

Показатели качества	Перерегулирование σ , %	Время переходного процесса tp	Коэффициент усиления  K
Желаемые	14	22	57
Полученные	38.4	9.57	17

Из анализа качества системы автоматического управления видно, что исходная система не удовлетворяет заданным показателям качества. Повысить качество процесса регулирования можно с помощью синтеза САУ, то есть  необходимо изменить динамические свойства системы регулирования с помощью корректирующих устройств. 

4. Синтез коррекирующих устройств

Рассмотрим синтез САУ с помощью включения корректирующих устройств в виде параллельного звена.

Параллельное корректирующее устройство будем подключать ко второму звену.

Строим располагаемую ЛАЧХ – L(w)=20log(W(jw)):

От высот 20 log K = 20 log 17= 24 по оси L, дБ/дек до частоты

log w₁=log 1/T₁ =log 1/7.7 = -0.88 проводим прямую с наклоном 0 дб/дек.

Начиная с w₁ до частоты log w₂ = log 1/2 = 0.22 – проводим прямую с наклоном –20 дБ/дек. И начиная с w₂ – проводим прямую с наклоном                 –40дБ/дек.

Строим желаемую ЛАЧХ:

В интервале средних частот желаемая ЛАЧХ определяется заданными значениями перерегулирования и временем переходного процесса. Из соображения приближения реального процесса к оптимальному наклон среднечастотной асимптоты желаемой ЛАЧХ берут равным –20 дБ/дек.  

Максимальное значение 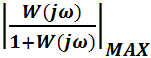         представляет собой показатель колебательности М_MAX. Считается, что в хорошо демпфированных системах регулирования показатель колебательности не должен превосходить значение 1,1-1,5. Примем М=1,2. Примем n=1. Частоту среза ω_сp найдем для заданных значений перерегулирования и времени регулирования:

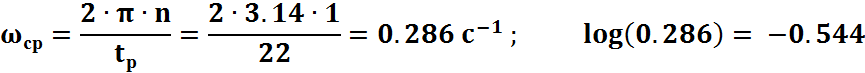
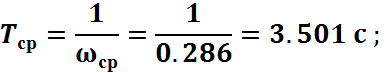
Граничные значения сопрягающих частот среднечастотной области найдем по формулам, где М = 1.2 – показатель колебательности:

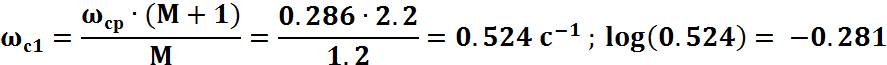
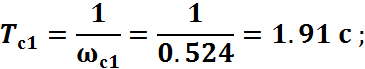
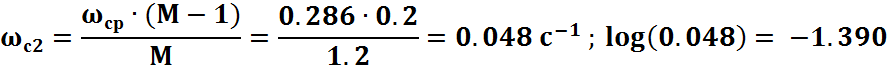
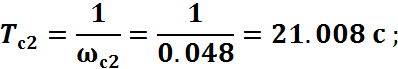
Сопряжение среднечастотной области с высокочастотной осуществляется переносом высокочастотной области ЛАЧХ в правую границу ω_c1, среднечастотной области. В низкочастотной области для получения желаемого коэффициента усиления вводим добавочную сопрягающую частоту ω*=0.017c^-1 и Т*=60.

 

ЛАЧХ располагаемой, желаемой САУ и корректирующего устройства