Направленные ответвители и мосты сложения, страница 3

Квадратные мосты сложения широко используются для деления ВЧ мощности поровну от одного входа на два выхода, и, обратно, для сложения двух равных входных  сигналов от отдельных усилительных модулей в один выход. Рассмотрим квадратный двухшлейфный мост, построенный из четвертьволновых отрезков линий с волновыми сопротивлениями 1R₀ и 0.707R₀, где R₀ - сопротивление нагрузки, на которую согласованы линии, присоединенные к ответвителю. 

Порядок действий стандартный:

1)  находим матрицы передачи для синфазного и противофазного сигнала

2)  их преобразуем в соответствующие S-матрицы для синфазного и противофазного сигнала

3)  по указанному правилу объединяем S-матрицы четырехполюсников синфазного и противофазного возбуждения в S-матрицу симметричного восьмиполюсника  - данного двухшлейфного направленного ответвителя.

1 Матрица эквивалентной схемы для противофазного возбуждения - При противофазном возбуждении по входам 1 и 3, в вертикальных шлейфах между клеммами 1 и 4, а так же 2 и 4 оказывается 0 напряжения - т.е. условное "кз" посередине, и линии передачи противофазного сигнала  соответствует четырехполюсник с матрицей передачи, равной произведению  трех матриц, представляющих  три последовательных  элемента: индуктивный шлейф l/8 с , линию l/4  с  и снова индуктивный шлейф l/8 с :

.              

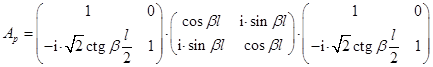В результате перемножения этих матриц получаются следующие выражения для элементов матрицы A_p:

;                

 ;

;.

2 Матрица эквивалентной схемы для синфазного возбуждения Перемножим последовательно - две одинаковые матрицы на концах - матрицы параллельного включения реактивности разомкнутого шлейфа l/8, между ними вставим матрица передачи четвертьволновой линии с r =1.  Вносимая хх шлейфами  параллельная емкостная реактивность  :

                   

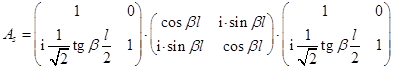
В результате перемножения этих матриц получаются следующие выражения для элементов матрицы A_s:

;

;

;

.

Подстановка этих выражений в формулы (10)ё(13) дает выражение коэффициентов передачи 3дБ квадратного моста. Они оказываются весьма громоздкими даже для случая, когда A-матрицы получаются перемножением всего трех элементарных матриц.

Абсолютная величина коэффициентов S-матрицы 3дБ квадратного                    моста на распределенных линях

То же самое в терминах  формул (1.1)ё(1.4)

Направленный ответвитель на связанных линиях

Пусть на протяжении длины l две одинаковые ТЕМ линии имеют определению и постоянную по величине электрическую и магнитную связь. Величину этой связи (взаимную погонную емкость и индуктивность) полностью характеризуют волновые сопротивления получившейся трехпроводной линии для синфазного Z_M и противофазного  Z_E возбуждения. Эти волновые сопротивления для разных поперечных сечений трехпроводной линии можно вычислить конформными отображениями или легко измерить на макете в электролитической ванне. (Если в горизонтальный плоский сосуд ровным слоем налить плохо проводящую жидкость – например водопроводную воду, и поставить металлические стенки, то измеренные омметром сопротивления между ними будут пропорциональны соответствующим волновым сопротивлениям , . При этом коэффициент пропорциональности С необходимо измерить в этой же ванне на эталонном макете линии с известным волновым сопротивлением – например коаксиала . Схема включения и сопоставление результата измерения волновому сопротивлению показаны на рисунке.)