Аналогично, для синфазного сигнала, то есть для сигнала с совпадающей амплитудой и фазой в обоих входах, на линии симметрии установится ноль тока, и все пересекающие плоскость симметрии связи можно мысленно разорвать, и установить на концах оборванных связей режим холостого хода.
|
|
Два варианта четырехполюсников, получившиеся после раздела восьмиполюсника, описываются матрицей передачи, учитывающей параллельное подключение проводимостей оборванных линий связи – шлейфов. Этот метод будет использован в дальнейшем изложении. Явный пример этого приема – анализ квадратного моста – показан на прилагаемом рисунке 3, матрицы для соответствующих четырехполюсников и восьмиполюсника даются в следующей главе.
Рисунок 1.3 Получение четырехполюсников для синфазного и противофазного сигнала из схемы восьмиполюсника квадратного моста.
Матрицы передачи обозначаются заглавной
буквой А, матрицы рассеяния заглавной буквой S. Элементы
нормированной матрицы A, как принято, обозначаются a,b,c,d,
и связывают нормированные токи и напряжения, имеющие одинаковую размерность 
на выходе и входе четырехполюсника:
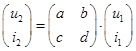
Для получения общей матрицы, описывающей результат каскадного (последовательного или цепного) подключения четырехполюсников, их матрицы передачи перемножаются в порядке соединения четырехполюсников. Для составления всех матриц передачи, используемых здесь в дальнейшем, нам понадобятся только следующие три вида A-матрицы элементарных 4-полюсников :
–матрица передачи отрезка линии длиной l и волновым сопротивлением r:
,
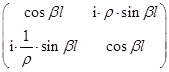– матрица
последовательного включения импеданса z : 
,
– матрица
параллельного включения проводимости y : 
.
Параллельные l/8 шлейфы, которые получаются при делении l/4 линий симметричного 8-полюсника на 4-полюсники для синфазного и противофазного сигнала, описываются матрицей №5 со следующими величинами реактивной проводимости: для короткого замыкания, и холостого хода на конце шлейфа, соответственно
, 
.
Матрицы различного типа, описывающие один и тот же четырехполюсник, однозначным образом преобразуются друг в друга. Соотношения между матрицами 4-полюсников СВЧ даны в Таблице 3.1 [Д.М. Сазонов и др. «Устройства СВЧ»]. Элементы S-матрицы выражаются через элементы А-матрицы следующим образом:
.
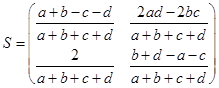S-матрица симметричного 8-полюсника, размером 4ґ4 получается симметричной комбинацией четырех матриц размером 2ґ2 двух типов S1 и S2:
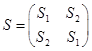, где 
получаются из матрицы
4-полюсника для синфазного возбуждения и матрицы 
для 4-полюсника противофазного возбуждения. ( § 3.6 того же
источника [Д.М. Сазонов и др. «Устройства СВЧ»]). Ввиду явной симметрии
рассматриваемых схем, нам достаточно узнать только первый столбец матрицы
рассеяния, описывающий коэффициенты передачи от первого входа. Любой другой
вход можно поставить на место первого переворотом и (или) отражением.
Для четырех интересующих нас элементов S-матрицы получаются следующие выражения через элементы матриц Аs синфазного сигнала и Аs противофазного:
, 
, 
,
.
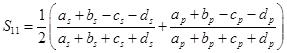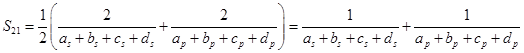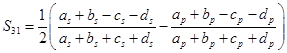Таким образом, анализ схем ответвителей сводится к нахождению выражений для элементов А-матриц As и Ap, и, затем, комбинирования их в S по данной процедуре.
|
|
Двухшлейфный квадратный мост 3дБ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
