Курсовая работа по курсу "Роботехнические системы и комплексы" (Построение и моделирование математических моделей каналов)

Санкт – Петербургский Институт Точной Механики и Оптики

(Технический Университет)

Кафедра Систем Управления и Информатики

Курсовая работа

по курсу Роботехнические системы и комплексы

      Выполнила:

     Группа: 545

           Преподаватель:

Санкт – Петербург, 2002

Задание:

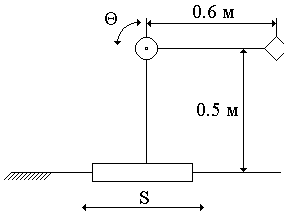
Рис. 1

Выбор систем координат:

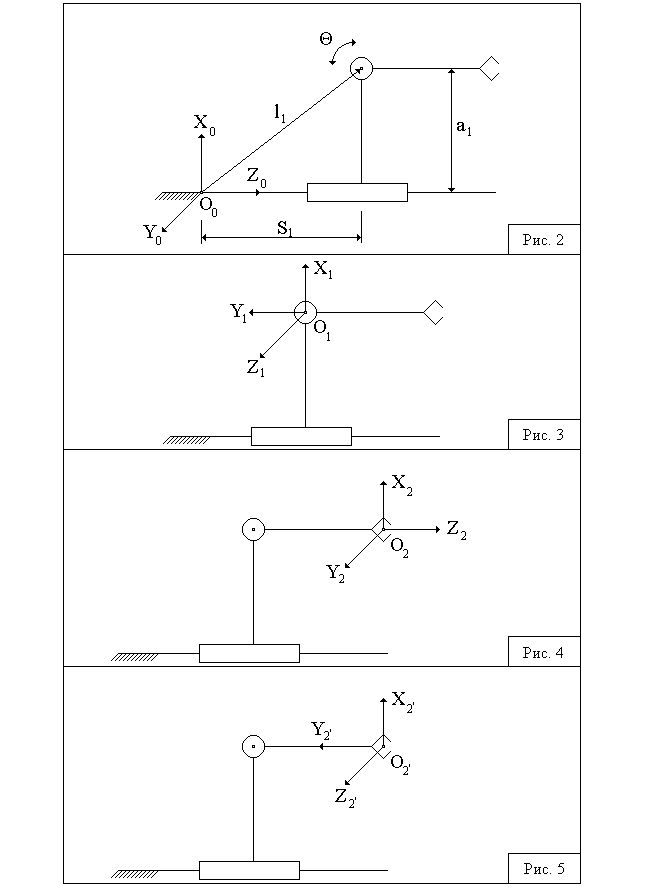
Формулы перехода:

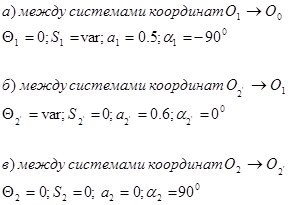
Вычисления:

Вычисление r_сх:

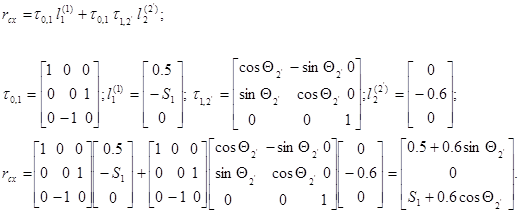Вычисление относительной угловой скорости:

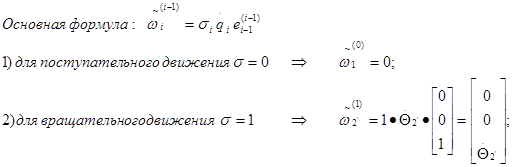Вычисление относительной линейной скорости:

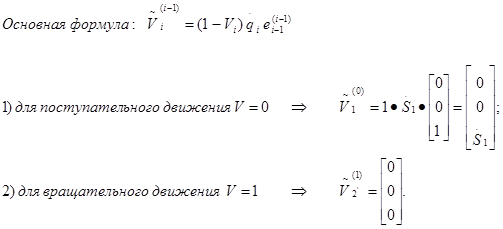
Вычисление абсолютной угловой скорости:

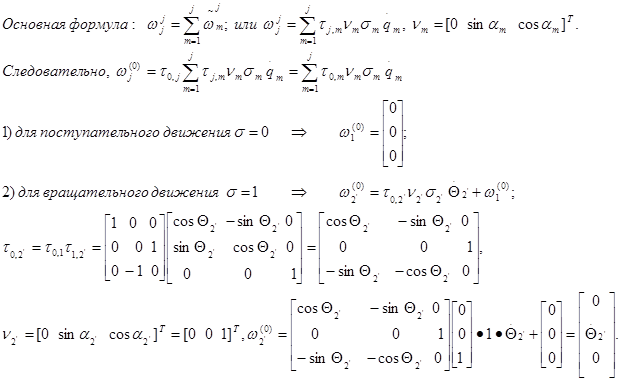
 Вычисление абсолютной линейной скорости:

Построение блочных матриц

Построение блочного вектора:

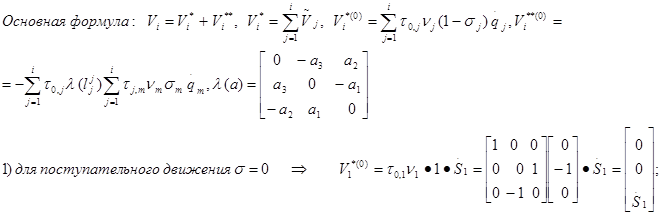
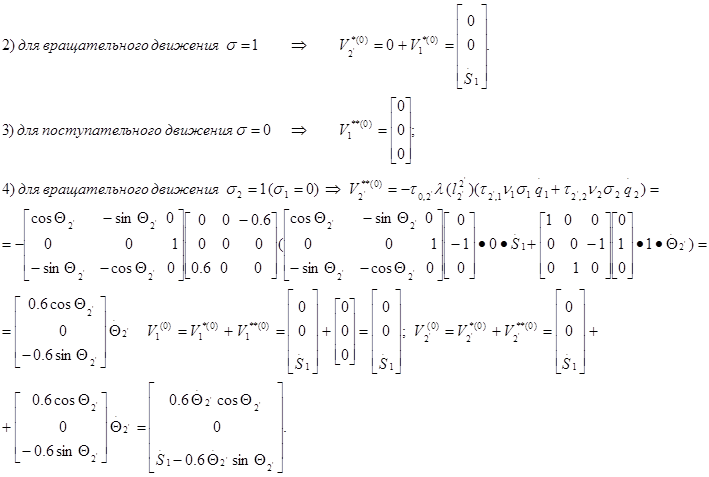
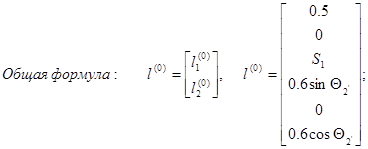
Построение блочных матриц:

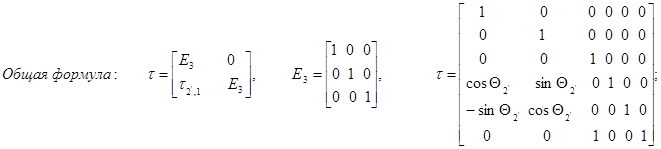
Вычисление матриц A(q) и D(q):

Вычисление матрицы A(q):

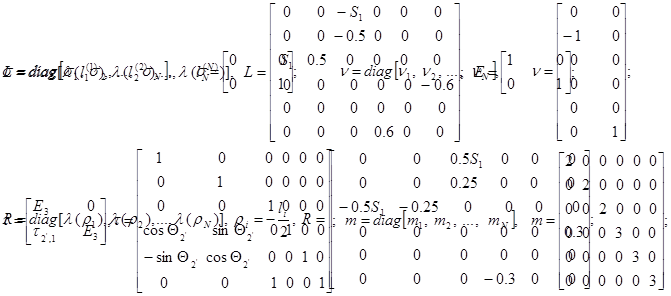Расчет моментов инерции цельного стержня (m₁= 2 кг, m₂= 3 кг, h₁= 0.5 м, h₂= 0.6 м, R= 0.005 м)

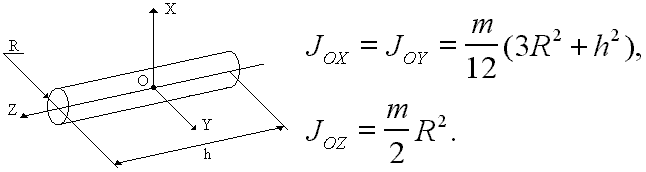
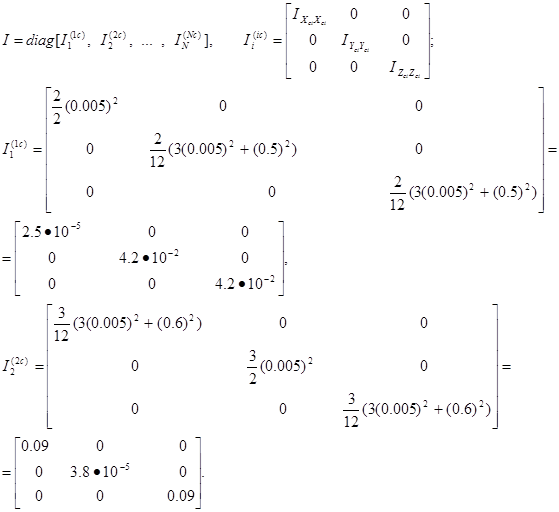
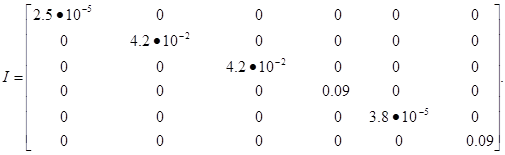
Расчет матрицы A(q):

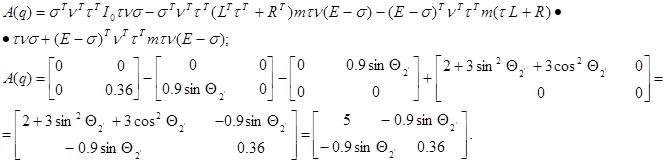
Вычисление матрицы D(q):

Моделирование:

   

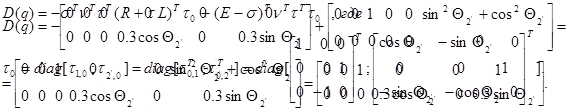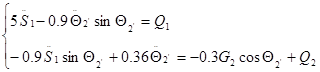
Построение математической модели:

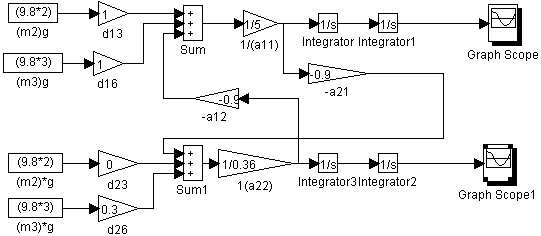
Рис. 1. Математическая модель нескорректированной системы.

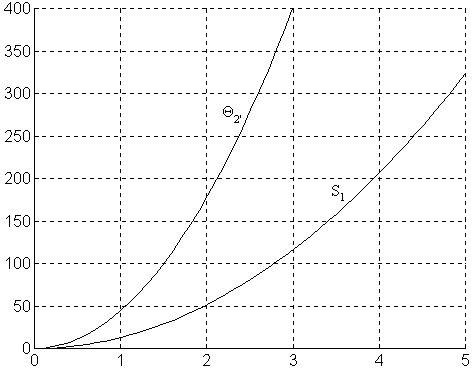
Рис. 2. Результаты моделирования.

Вычисление максимальных значений моментов:

а_11(max) = 5;      а_12(max) = а_21(max) = (Θ_2’ = 90⁰) = -0.9;             а₂₂ = 0.36;       d₁₃ = d₁₆ = 1;               d₂₃ = 0;

d_26(max) =  (Θ_2’ = 90⁰) = 0.3

Выбор двигателя:

Выбираем двигатель постоянного тока ДПР-72-H1-03,   технические данные которого приведены в Таблице1.

Таблица1. Технические данные двигателя ДПР-72-H1-03.

По расчетам, оптимальное передаточное число редуктора i = 1. Суммарный момент инерции ; J_ДВ=0.6*10^-4Нм²; 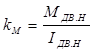=0.041; =0,052; R_Я = 2.9Ом.

Построение и моделирование математических моделей каналов:

1.  Для первого канала применим пропорционально-интегральный регулятор:

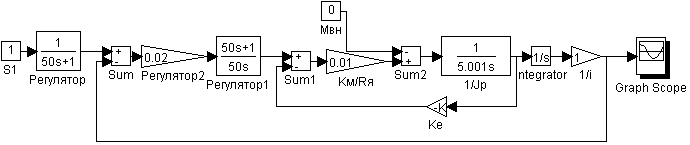
Рис. 3. Схема моделирования первого канала системы с пропорционально-интегральным регулятором без возмущающего воздействия (M_ВН = 0); , К_рег = 0.02.

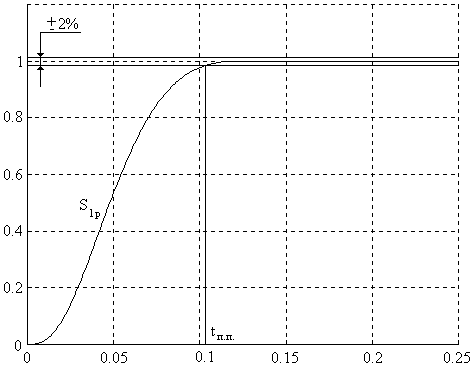
Рис. 4. Результаты моделирования по первому каналу: перерегулирование σ = 0%, t_п.п. = 0.105 с.

2.  Для второго канала также применим пропорционально-интегральный регулятор:

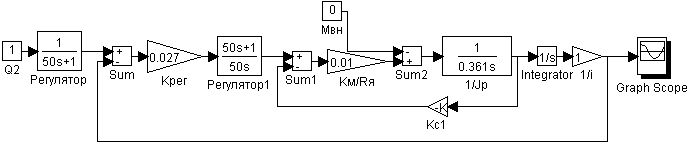
Рис. 5. Схема моделирования второго канала системы с пропорционально-интегральным регулятором без возмущающего воздействия (M_ВН = 0); , К_рег = 0.027.

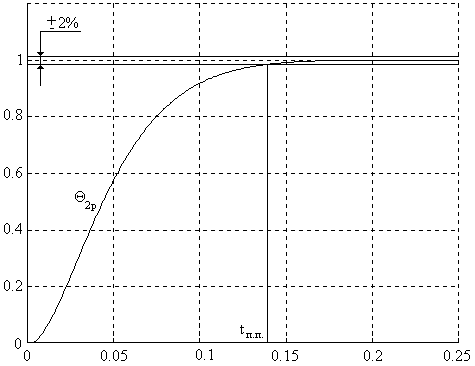
Рис. 6. Результаты моделирования по второму каналу: перерегулирование σ = 0%, t_п.п. = 0.135 с.

3.  Проделаем те же эксперименты, но с возмущающим воздействием:

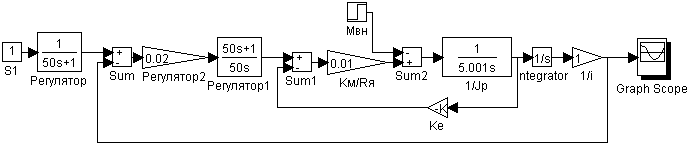
Рис. 7. Схема моделирования первого канала без комбинированного регулятора по возмущению.

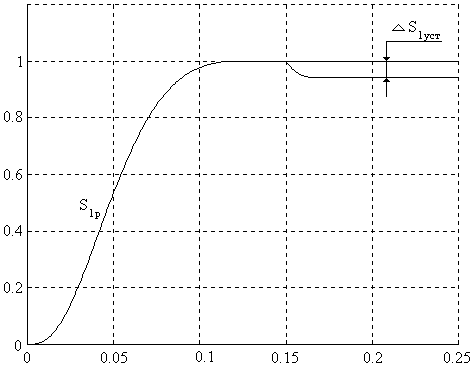
Рис. 8. Результаты моделирования: установившаяся ошибка

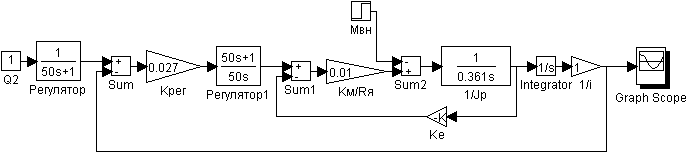
Рис. 9. Схема моделирования второго канала без комбинированного регулятора по возмущению.

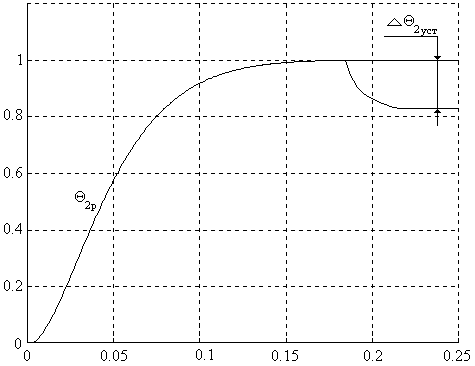
Рис. 10. Результаты моделирования: установившаяся ошибка

4. Проверим астатизм системы.

1) Отработка линейно-нарастающего воздействия:

а) для первого канала:

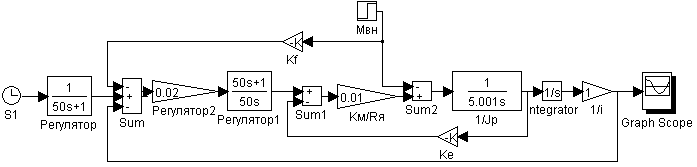
Рис. 11. Схема моделирования отработки линейно-нарастающего воздействия первым каналом с комбинированным регулятором по возмущающему воздействию.

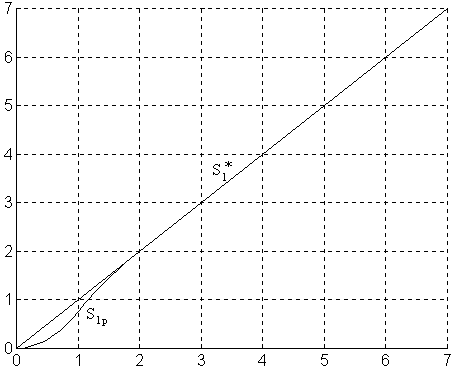
Рис. 12. Результаты моделирования: установившаяся ошибка ΔS_уст = 0.

б) для второго канала:

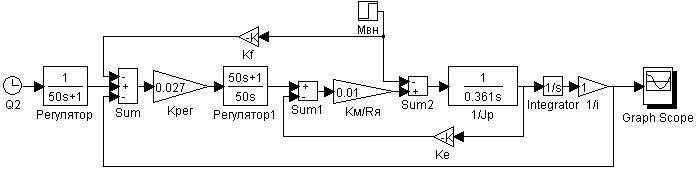
Рис. 13. Схема моделирования отработки линейно-нарастающего воздействия вторым каналом с комбинированным регулятором по возмущающему воздействию.

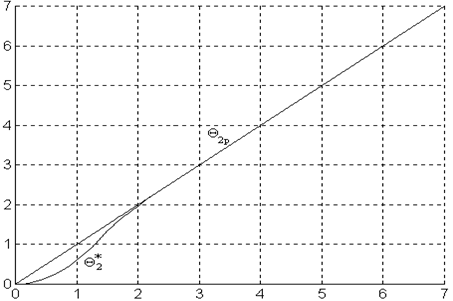
Рис. 14. Результаты моделирования: установившаяся ошибка ΔΘ_уст = 0.

2) Отработка нелинейного входного воздействия:

а) для первого канала:

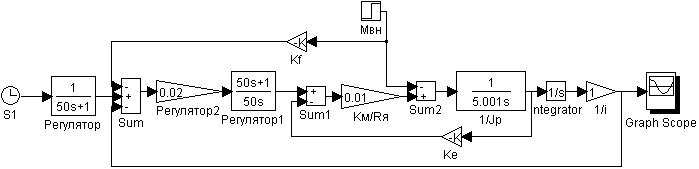
Рис. 15. Схема моделирования отработки нелинейного входного воздействия первым каналом с компенсацией задающего  и возмущающего воздействий.

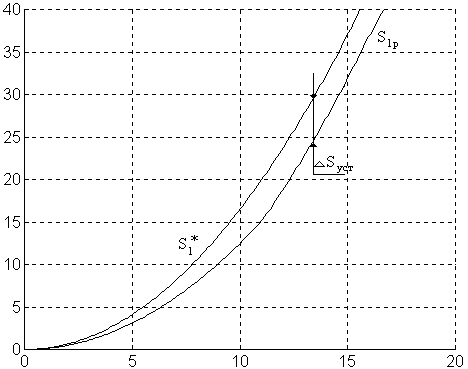
Рис. 16. Результаты моделирования: установившаяся ошибка ΔS_уст = 5.

б) для второго канала:

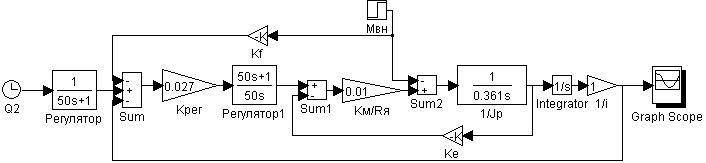
Рис. 17. Схема моделирования отработки нелинейного входного воздействия вторым каналом с компенсацией задающего  и возмущающего воздействий.

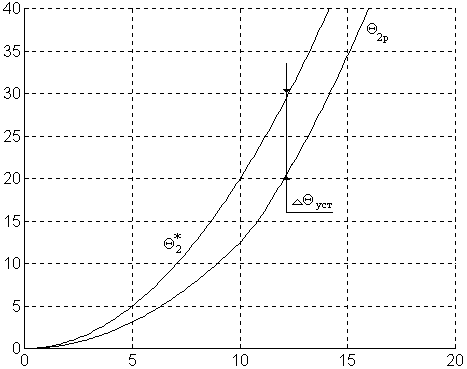
Рис. 18. Результаты моделирования: установившаяся ошибка ΔΘ_уст = 10.

Вывод: результаты моделирования первого и второго каналов при отработке линейных входных воздействий (константы и линейно-нарастающего) показывают, что система имеет порядок астатизма по отношению ко входному воздействию не ниже первого; отработка нелинейного воздействия – с ненулевой постоянной ошибкой при компенсации и возмущающего, и задающего воздействия – позволяет предположить, что порядок астатизма системы не выше второго.

Общий вывод – система имеет порядок астатизма по отношению ко входному воздействию, равный двум (υ=2).

Моделирование решения прямой задачи кинематики: