







8.3. Образование и изображение поверхностей вращения
Поверхности вращения образуются вращением образующей линии l вокруг неподвижной прямой i - оси вращения (рис.63). Эти линии называются определителем поверхности вращения.
Поверхности вращения могут быть линейчатыми (например, конус или цилиндр) и нелинейчатыми или криволинейными (например, сфера). Линейчатые поверхности можно развернуть на плоскость без складок и разрывов.
![]()
![]()
![]()
![]()
![]() i i
i i
![]()
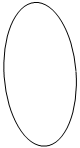


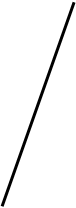

![]()
![]()
![]()
![]()
![]()
 i
i
 |
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() l
l

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
l l
Рис. 63
Криволинейная поверхность вращения образуется при вращении любой кривой вокруг оси (рис. 64).
![]()
![]()
![]()
![]()

![]()

 i
i
i
i
![]()
![]() образующие
образующие
![]()
![]()
Рис. 64
Пример. Построить горизонтальную проекцию прямого кругового цилиндра по заданным проекциям. Определить недостающие проекции точек, находящихся на его поверхности (рис. 65, а).
Алгоритм решения задачи
1.По двум заданным проекциям цилиндра можно построить его горизонтальную проекцию с помощью биссекторной плоскости (рис.65, б).
2.Сделаем анализ расположения точек А, В, С на поверхности вращения.
3. (·) С принадлежит верхнему основанию цилиндра, которое проецируется в прямую линию на фронтальной и горизонтальной плоскостях проекций => фронтальная проекция (·) С2 и горизонтальная проекция (·) С1 будут принадлежать верхнему основанию.
а) Дано: б) Решение задачи:
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 z
z А3
z
z А3
![]()
![]()
![]()
![]()
![]() А2
А2
А2
А2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() cс′
cс′
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() В2
С3 С2 В2
С3
В2
С3 С2 В2
С3
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]() В3
В3
x y x y
![]()
![]()
![]()
![]()
![]() В1
В1
![]()
![]()
![]()
![]() С1
А1
С1
А1
Рис. 65
4. (·) В принадлежит крайней образующей цилиндрической поверхности, то есть профильному очерку цилиндра – окружности (так какi ┴ П2) => профильная проекция (·) В3 , принадлежит окружности.
5. Горизонтальную проекцию точки В - (·) b1 необходимо найти с помощью линий связи.
6. (·) А принадлежит цилиндрической поверхности, => через фронтальную проекцию (·) А2 можно провести образующую и найти профильную проекцию (·) А3 , которая проецируется на профильный очерк цилиндрической поверхности.
6. Горизонтальную проекцию точки А - (·) А1 необходимо найти с помощью линий связи.
7. Видимость точек определяется по правилу конкурирующих точек. В данном примере все точки на поверхности цилиндра видимы.
Пример . По заданной образующей (SK), оси вращения (I) и точки М, принадлежащей конической поверхности, построить проекции прямого кругового конуса, основание которого принадлежит фронтальной плоскости проекций (рис.66, а).
Алгоритм решения задачи
1. По условию задачи ось конической поверхности вращения (рис.66, a) перпендикулярна фронтальной плоскости проекций. При вращении образующей (SK) вокруг оси (i) получается конус. На горизонтальную плоскость проекций эта поверхность проецируется в треугольник, а на фронтальную в окружность с радиусом вращения (S2 K2).
![]()
![]()
![]() а) Дано: б) Решение
задачи:
а) Дано: б) Решение
задачи:

![]()

![]()
 S2≡ i2 h3
S2≡ i2 h3
![]() h2
h2 

![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() K2 S2≡ i2
S3
K2 S2≡ i2
S3
![]()
![]()
![]() M2
M3
M2
M3
![]()
![]()
![]() 12
13
12
13
![]()

![]()


![]() K1
1
K1
1
![]() • M1
h1 M1
• M1
h1 M1
 |
![]() S1
i S1 i
S1
i S1 i
Рис. 66
2. По горизонтальной и фронтальной проекциям конуса строим его профильную проекцию. Она отображается треугольником (рис.66, б).
3.
(•) М принадлежит поверхности прямого кругового
конуса =>, ее проекции принадлежат соответствующим проекциям образующих
конической поверхности. Горизонтальная проекция (·)M ![]() S1K1, фронтальная –
M2
S1K1, фронтальная –
M2 ![]() S2K2 и профильная
проекция M3
S2K2 и профильная
проекция M3 ![]() S3K3.
S3K3.
4. Можно определить проекции точки М еще одним способом – с помощью дополнительной горизонтальной секущей плоскости (h), которая перпендикулярна оси вращения и параллельна основанию. Фигура сечения поверхности данной плоскостью проецируется на фронтальную плоскость проекций в виде окружности, а на две другие плоскости – в виде прямых линий.
Пример. Построить три проекции поверхности, образованной вращением окружности заданного радиуса R, вокруг оси i. Найти недостающие проекции точек (А, В, С, D, E), принадлежащих данной поверхности (рис. 67, а).
Алгоритм решения задачи
1. Вращением окружности (образующей) вокруг оси симметрии образуется поверхность вращения – сфера. Крайний очерк сферы на фронтальной, горизонтальной и профильной плоскостях проекций имеет форму окружности. Используя линии связи, можно построить три проекции сферы заданного радиуса R (рис. 67, а). Для построения проекций точек необходимо провести анализ расположения точек на поверхности вращения.

![]()

![]() а)
Дано: R
i С
а)
Дано: R
i С

![]()
![]() E≡D
E≡D
![]()
![]()
![]()
![]() В
В
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.