Высшая математика. Первый семестр: Интерактивный компьютерный учебник (Функции и их графики. Непрерывность функций и точки разрыва)

множество всевозможных пар называется прямым произведением множества A на множество B и обозначается A×B.

Ясно, что график функции f — это подмножество прямого произведения A×B:

= {(x;y) A×B : y = f (x)}A×B.

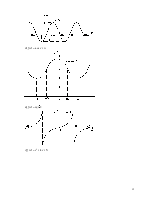
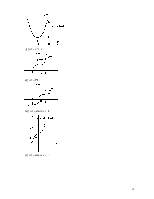
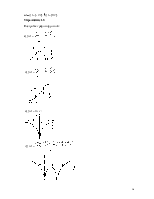
В некоторых из рассмотренных выше примеров функций были приведены на рисунках графики этих функций. График примера 1.2 — подмножество в ×[- 1;1]; график примера 1.3 — подмножество в × = ²; оба графика примера 1.6 — подмножества в ₊×₊ = ₊² (здесь мы ввели обозначение ₊ = [0; + ), которого будем придерживаться и далее).

Пример 1.8.

Пусть A — круг радиуса 1 (включая окружность радиуса 1 — границу круга) на числовой плоскости ² с координатами x₁ и x₂, с центром в точке O(0;0). Функцию f в любой точке круга зададим как расстояние от этой точки (x₁;x₂) до центра. Таким образом, f (x) = , где x = (x₁;x₂) AR².

Графиком этой функции является подмножество прямого произведения A×. Это прямое произведение — бесконечный цилиндр с круговым сечением, находящийся в пространстве ²× = ³. Обозначим координаты точек в ³ через x₁, x₂, y. Тогда графику принадлежат те точки, для которых выполнены соотношения y = и x₁² + x₂² 1.

Множество Г_f представляет собой кусок конической поверхности с вершиной в точке (0;0;0), с высотой 1 и радиусом основания 1.

Рис.1.7. График расстояния до точки O — это конус

Как мы видим, в случае, когда A — подмножество плоскости ², график числовой функции f : A — это подмножество точек пространства ³. Если же A — подмножество точек пространства ³, то графиком числовой функции f : A будет подмножество четырёхмерного пространства, точнее, его подмножества A×³× = ⁴. В связи с этим, изобразить график такой функции на чертеже не представляется возможным, хотя, конечно, можно постараться как-то этот график описать каким-то иным способом.

Пример 1.9.

Пусть A = ³ и для каждой точки x = (x₁;x₂;x₃) ³ значение функции f в этой точке — это квадрат расстояния от x до точки O(0;0;0), то есть f (x) = x₁² + x₂² + x₃² = | x|². Тогда график — это подмножество в ⁴:

= {(x₁, x₂, x₃, y) ⁴ : y = x₁² + x₂² + x₃²}.

Изобразить этот график, то есть нарисовать трёхмерную поверхность, расположенную в четырёхмерном пространстве, мы уже не в состоянии, однако формула y = x₁² + x₂² + x₃² позволяет изучать этот график. Например, можно заметить, что двумерное сечение этого графика плоскостью

{(x₁, x₂, x₃, y) ⁴ : x₂ = 0, x₃ = 0} — это парабола y = x₁² в плоскости x₁Oy, а сечение трёхмерным пространством {(x₁, x₂, x₃, y) ⁴ : y = 0} — это одна точка (0;0;0;0).

Наибольший интерес с точки зрения наглядности представляют графики числовых функций одного переменного. Изучению поведения таких функций и построению их графиков будет уделено основное внимание в следующих главах.

Как мы видим из приведённых выше примеров, способы эти могут быть самые разные, от словесно-описательного в примерах 1.1, 1.4 до задания функции формулой вида y=f (x) в примерах 1.2, 1.3, 1.6, 1.8, 1.9. Способ задания функции f : AB зависит от того, какова природа множеств A и B и как по заданному x A определяется y=f (x) B. Выделим основные из этих способов.

1.2. Первый способ задания функции: табличный

Если множество A = (f ) конечно и состоит из N элементов x₁, x₂,..., x_N, то функцию можно задать перечислением, указав, какие значения она принимает на каждом элементе x A. Часто это делают в виде таблицы:

В верхней строке таблицы перечисляются все N элементов конечного множества A, а в нижней — соответствующие им значения функции. Разумеется, таблицу можно расположить и в два столбца вместо двух строк.

Пример 1.10.

В отделе кадров составляют таблицу, в которой в первом столбце содержатся фамилии и инициалы работников, а во втором — серии и номера их паспортов. Такая таблица задаёт функцию f — соответствие между множеством A работников предприятия и множеством B кодов (код — это серия и номер) паспортов. Полученная таблица может выглядеть, например, так:

Определённая таким способом функция f — это инъекция, так как ни у каких двух человек не могут оказаться паспорта с одинаковым кодом (серия, номер).

Другая форма таблицы удобна для функции f : AB, заданной на прямом произведении двух множеств A₁ и A₂, то есть когда A = (f )= A₁×A₂, причём множества A₁ и A₂ конечные: A₁ = {x₁⁽¹⁾, x₁⁽²⁾,..., x₁^(m)} и A₂ = {x₂⁽¹⁾, x₂⁽²⁾,..., x₂⁽ⁿ⁾}. Перечислим все элементы множества A₁ по вертикали, а A₂ — по горизонтали. В пересечениях строки и столбца, содержащих элементы