Высшая математика часть 2
СОДЕРЖАНИЕ
4. Производные и дифференциалы
4.1. Мгновенная скорость при прямолинейном движении
4.2. Касательная к кривой на плоскости
4.3. Производная
4.4. Свойства производных
4.5. Производные некоторых элементарных функций
4.6. Дифференциал
4.7. Производная композиции
4.8. Инвариантность дифференциала
4.9. Производная обратной функции
4.10. Производные некоторых элементарных функций (продолжение)
4.11. Сводка основных результатов о производных
4.12. Производные высших порядков
4.13. Дифференциалы высших порядков и их неинвариантность
4.14. Производные функции, заданной параметрически
4.15. Производная функции, заданной неявно
4.16. Приближённое вычисление производных
4.17. Примеры и упражнения
5. Свойства дифференцируемых функций
5.1. Четыре теоремы о дифференцируемых функциях
5.2. Правило Лопиталя
5.3. Сравнение бесконечно больших величин
6. Формула Тейлора
6.1. Многочлен Тейлора
6.2. Остаток в формуле Тейлора и его оценка
6.3. Формула Тейлора для некоторых элементарных функций
6.4. Оценки ошибок в формулах приближённого дифференцирования
6.5. Упражнения
7. Исследование функций и построение графиков
7.1. Асимптоты графика функции
7.2. Возрастание и убывание функции
7.3. Экстремум функции и необходимое условие экстремума
7.4. Достаточные условия локального экстремума
7.5. Выпуклость функции
7.6. Общая схема исследования функции и построения её графика
7.7. Примеры исследования функций и построения графиков
7.8. Упражнения и задачи
Производные и дифференциалы
Здесь мы переходим к изучению производной — одного из двух важнейших понятий, наряду с интегралом, на которых держится весь современный математический анализ.
Понятие производной связано с понятием скорости в механике и с понятием касательной к кривой в геометрии. Разберём эту связь по порядку.
4.1. Мгновенная скорость при прямолинейном движении
Пусть
материальная точка движется по координатной прямой Oy, и её положение в
момент времени x имеет координату y = f (x). Средняя
скорость точки за произвольный промежуток времени [x0;x1],
за который точка перемещается из положения y0 = f (x0)
в положение y1 = f (x1),
определяется как v[x0;x1] = ![]() . Если мы обозначим
протекший промежуток времени через h, то x1 = x0
+ h и y1 - y0 = f (x0
+ h) - f (x0), поэтому v[x0;x0 + h]
=
. Если мы обозначим
протекший промежуток времени через h, то x1 = x0
+ h и y1 - y0 = f (x0
+ h) - f (x0), поэтому v[x0;x0 + h]
= ![]() , при h
> 0. Мгновенная скорость точки в момент x0
определяется как предел средней скорости за промежуток времени от x0
до x0 + h (h > 0), при условии h
, при h
> 0. Мгновенная скорость точки в момент x0
определяется как предел средней скорости за промежуток времени от x0
до x0 + h (h > 0), при условии h![]() 0. Таким
образом, получаем формулу, служащую определением мгновенной скорости в момент x0:
0. Таким
образом, получаем формулу, служащую определением мгновенной скорости в момент x0:
|
v+(x0) = |
(4.1) |
Можно
также рассматривать промежутки времени, протекшие до момента x0,
то есть промежутки от x0 - h до x0.
Тогда средняя скорость точки y за этот промежуток времени будет равна v[x0
- h;x0] = ![]() , при h
> 0. Если положить k = - h < 0, то, очевидно, v[x0
+ k;x0] =
, при h
> 0. Если положить k = - h < 0, то, очевидно, v[x0
+ k;x0] = ![]() , при k
< 0. При этом придётся определять мгновенную скорость в момент x0
формулой
, при k
< 0. При этом придётся определять мгновенную скорость в момент x0
формулой
|
v-(x0) = |
(4.2) |
Определение 4.1.
Число v+(x0) мы будем называть правой производной, или производной справа, функции f (x) в точке x0 и обозначать f'+(x0) или f'(x0 +), а число v-(x0) — левой производной, или производной слева, функции f (x) в точке x0 и обозначать f'-(x0) или f'(x0 -). Иногда для уточнения говорят, что эти производные вычислены по переменной x.
Напомним
ещё раз, что механический смысл как левой, так и правой производной координаты y
= f (x) по времени x — это мгновенная скорость движения,
вычисленная в момент x0, но либо по интервалам времени,
предшествующим x0, либо по интервалам, последующим x0.
Эти две мгновенных скорости не обязаны, вообще говоря, совпадать: если тело покоилось
до момента x0, а затем двинулось с постоянной скоростью v
> 0, то мгновенная скорость, вычисленная по предшествующим интервалам,
очевидно, равна f'-(x0) = 0 (так как до
момента x0 тело покоилось), а мгновенная скорость,
вычисленная по последующим интервалам времени, равна f'+(x0)
= ![]()
![]() = v
(vh — это изменение координаты y точки, движущейся со скоростью v,
за промежуток времени продолжительности h с момента x0
до момента x0 + h). Эти две мгновенных скорости
различны.
= v
(vh — это изменение координаты y точки, движущейся со скоростью v,
за промежуток времени продолжительности h с момента x0
до момента x0 + h). Эти две мгновенных скорости
различны.
4.2. Касательная к кривой на плоскости
Пусть на
координатной плоскости xOy построен график функции f (x),
и x0 — некоторая внутренняя точка области определения ![]() (f
). Прямая, проходящая через точки M0(x0;y0)
и M1(x1;y1), где y0
= f (x0) и y1 = f (x1)
( x1
(f
). Прямая, проходящая через точки M0(x0;y0)
и M1(x1;y1), где y0
= f (x0) и y1 = f (x1)
( x1![]() x0),
— это секущая по отношению к графику y = f (x). Касательной
к линии y = f (x) в точке M0 называется
прямая M0N, служащая предельным положением секущих
(прямых M0M1), при условии, что точка M1
приближается, следуя по линии y = f (x), к точке касания M0.
x0),
— это секущая по отношению к графику y = f (x). Касательной
к линии y = f (x) в точке M0 называется
прямая M0N, служащая предельным положением секущих
(прямых M0M1), при условии, что точка M1
приближается, следуя по линии y = f (x), к точке касания M0.
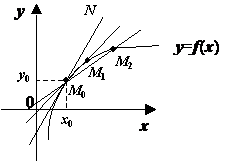
Рис.4.1. Касательная — это предельное положение секущих
Этому не
вполне строгому определению можно придать точный смысл, если задавать положения
всех прямых, проходящих через точку M0, то есть секущих и
касательной, их углом наклона по отношению к положительному направлению оси Ox.
Обозначим через ![]() угол наклона
прямой M0M1. Очевидно, что, вообще говоря,
угол
угол наклона
прямой M0M1. Очевидно, что, вообще говоря,
угол ![]() зависит от
выбора точки M1:
зависит от
выбора точки M1: ![]() =
= ![]() (x1)
(считаем, что точка M0 фиксирована). Так как секущая проходит
через точки с координатами (x0;f (x0))
и (x1;f (x1)), то
(x1)
(считаем, что точка M0 фиксирована). Так как секущая проходит
через точки с координатами (x0;f (x0))
и (x1;f (x1)), то
tg ![]() (x1)
=
(x1)
= ![]() .
.
Если теперь обозначить через h приращение абсциссы x при переходе от точки x0 к точке x1, то есть h = x1 - x0, то получим, что
tg ![]() (x0 + h) =
(x0 + h) = ![]() .
.
Приближение точки M1
к точке M0 вдоль кривой y = f (x)
означает, что h![]() 0; при
этом угол
0; при
этом угол ![]() приближается,
по определению, к углу
приближается,
по определению, к углу ![]() наклона
касательной M0N:
наклона
касательной M0N:
![]() =
= ![]()
![]() (x0
+ h).
(x0
+ h).
Предположим, что этот предел
существует (что означает существование касательной) и не равен ±![]() .
Тогда, вследствие того, что тангенс непрерывен при x
.
Тогда, вследствие того, что тангенс непрерывен при x![]() ±
±![]() + 2m
+ 2m![]() ( m
( m
![]()
![]() ),
получаем, что
),
получаем, что
tg ![]() =
= ![]() tg
tg ![]() (x0 + h) =
(x0 + h) = ![]()
![]() .
.
Итак, по
определению, мы называем прямую M0N наклонной
касательной (или просто касательной) к линии y = f (x)
в точке M0(x0;f (x0)),
если она имеет тангенс угла ![]() наклона к
оси Ox, равный
наклона к
оси Ox, равный
|
kx0 = tg |
(4.3) |
Число kx0 называют угловым коэффициентом касательной к графику функции при x=x0.
Если же ![]() =
= ![]()
![]() (x0
+ h) = ±
(x0
+ h) = ±![]() , то прямая
M0N оказывается вертикальной (перпендикулярной к оси Ox).
В этом случае будем говорить, что график y = f (x) имеет вертикальную
, то прямая
M0N оказывается вертикальной (перпендикулярной к оси Ox).
В этом случае будем говорить, что график y = f (x) имеет вертикальную
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.