Пусть требуется найти экстремумы функции ![]() при условии, что независимые переменные
связаны уравнениями
при условии, что независимые переменные
связаны уравнениями
![]() . (4.24)
. (4.24)
Такие экстремумы называются условными. Уравнения (4.24) называются уравнениями связи.
Условные экстремумы можно находить методом множителей Лагранжа, который состоит в следующем.
Запишем функцию, которую называют функцией Лагранжа:
![]() , (4.25)
, (4.25)
Коэффициенты ![]() называются множителями Лагранжа.
называются множителями Лагранжа.
Точки, «подозрительные» на условный экстремум, находятся из системы:
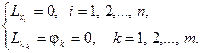 (4.26)
(4.26)
Пусть ![]() -
одна из таких точек. Чтобы выяснить, есть ли в этой точке условный экстремум,
исследуют второй дифференциал
-
одна из таких точек. Чтобы выяснить, есть ли в этой точке условный экстремум,
исследуют второй дифференциал ![]() при условиях
при условиях ![]() .
.
Рассмотрим частный случай. Пусть
требуется найти экстремум функции двух переменных ![]() при
условии
при
условии ![]() . Функция Лагранжа имеет вид:
. Функция Лагранжа имеет вид: ![]() . Точки, «подозрительные» на экстремум,
находятся из системы
. Точки, «подозрительные» на экстремум,
находятся из системы
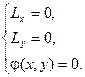
Предположим,
что ![]() - решение системы. Тогда точка
- решение системы. Тогда точка ![]() - точка, «подозрительная» на условный
экстремум.
- точка, «подозрительная» на условный
экстремум.
Чтобы определить, есть ли в этой точке экстремум, нужно вычислить определитель
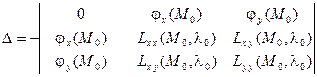 . (4.27)
. (4.27)
Если ![]() , то
, то ![]() -
точка условного максимума; если
-
точка условного максимума; если ![]() , то
, то ![]() - точка условного минимума.
- точка условного минимума.
Пример. Найти точки условного экстремума функции ![]() ,
если
,
если ![]() .
.
Функция Лагранжа имеет вид: ![]() .
.
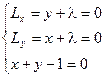
![]() .
.
Первый способ.
Проверим, существует ли экстремум функции в точке ![]() .
Найдем
.
Найдем ![]() .
. ![]() .
. ![]() . Следовательно, точка
. Следовательно, точка ![]() является точкой условного максимума.
Условный максимум
является точкой условного максимума.
Условный максимум ![]() .
.
Второй способ. Исследуем
второй дифференциал ![]() при условии
при условии ![]() . Так как
. Так как ![]() , то
, то ![]() . Следовательно, функция
. Следовательно, функция ![]() имеет условный максимум в точке
имеет условный максимум в точке ![]() , равный 1/4.
, равный 1/4.
Третий способ. Из
уравнения связи ![]() . Следовательно,
. Следовательно, ![]() . Это функция одного переменного
. Это функция одного переменного ![]() ,
, ![]() ,
, ![]() . В точке
. В точке ![]() функция
функция
![]() имеет максимум. Следовательно, функция
имеет максимум. Следовательно, функция ![]() в точке
в точке ![]() имеет
условный максимум.
имеет
условный максимум.
|
Рис. 1 |
Определение. Множество ![]() называется связным,
если любые его две точки можно соединить ломаной, целиком принадлежащей
множеству
называется связным,
если любые его две точки можно соединить ломаной, целиком принадлежащей
множеству ![]() .
.
Определение. Областью называется открытое связное множество.
На рисунке 1 даны примеры связного и несвязного множеств.
Пусть функция ![]() определена
и непрерывна на некотором ограниченном замкнутом связном множестве
определена
и непрерывна на некотором ограниченном замкнутом связном множестве ![]() и имеет на этом множестве, за исключением,
может быть, отдельных точек, конечные частные производные. Тогда на множестве
и имеет на этом множестве, за исключением,
может быть, отдельных точек, конечные частные производные. Тогда на множестве ![]() найдется точка
найдется точка ![]() ,
в которой функция принимает наибольшее (наименьшее) значение. Если точка
,
в которой функция принимает наибольшее (наименьшее) значение. Если точка ![]() лежит внутри множества
лежит внутри множества ![]() , то в ней функция имеет локальный
максимум (минимум). Но наибольшего (наименьшего) значения функция может
достигать и на границе множества
, то в ней функция имеет локальный
максимум (минимум). Но наибольшего (наименьшего) значения функция может
достигать и на границе множества ![]() . Поэтому, чтобы
найти наибольшее (наименьшее) значение функции, нужно найти точки, «подозрительные»
на экстремум, найти значения функции в этих точках, найти наибольшее
(наименьшее) значение функции на границе и сравнить полученные значения.
. Поэтому, чтобы
найти наибольшее (наименьшее) значение функции, нужно найти точки, «подозрительные»
на экстремум, найти значения функции в этих точках, найти наибольшее
(наименьшее) значение функции на границе и сравнить полученные значения.
|
Рис. 2 |
Пример. Найти наибольшее и наименьшее значения функции ![]() на
на
![]() , если
, если ![]() -
замкнутое множество, ограниченное прямыми
-
замкнутое множество, ограниченное прямыми ![]() .
.
1)
Найдем точки, «подозрительные» на экстремум. 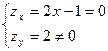 . Следовательно, функция не имеет
локальных экстремумов.
. Следовательно, функция не имеет
локальных экстремумов.
2)
Исследуем функцию на границе ![]() ,
, ![]() . Получаем
функцию
. Получаем
функцию ![]() ,
, ![]() . Так
как
. Так
как ![]() , то на границе
, то на границе ![]() нет
точек, «подозрительных» на экстремум. Найдем значения функции на концах отрезка
нет
точек, «подозрительных» на экстремум. Найдем значения функции на концах отрезка
![]() :
: ![]() .
.
3)
При ![]() получаем функцию
получаем функцию ![]() ,
, ![]() . Так
как
. Так
как ![]() , то
, то ![]() -
точка, «подозрительная» на экстремум.
-
точка, «подозрительная» на экстремум. ![]() .
. ![]() уже найдено ранее,
уже найдено ранее, ![]() .
.
4)
При ![]() получаем функцию
получаем функцию ![]() ,
, ![]() .
. ![]() . Так как
. Так как ![]() , то
точек, «подозрительных» на экстремум нет. Найдем значения функции на границе
отрезка.
, то
точек, «подозрительных» на экстремум нет. Найдем значения функции на границе
отрезка. ![]() найдено ранее,
найдено ранее, ![]() .
.
5)
Сравнивая полученные значения, находим ![]() . Наименьшее значение функция достигает
в точках (1/2, 0). Наибольшее значение функция достигает в точке (0, 1).
. Наименьшее значение функция достигает
в точках (1/2, 0). Наибольшее значение функция достигает в точке (0, 1).
Определение.
Обыкновенным дифференциальным уравнением (ОДУ) называется
уравнение, связывающее независимую переменную ![]() ,
искомую функцию
,
искомую функцию ![]() и ее производные
и ее производные ![]() .
.
ОДУ в неявной форме имеет вид
![]() . (5.1)
. (5.1)
Если из уравнения (5.1) можно выразить ![]() , то уравнение можно записать в явном
виде:
, то уравнение можно записать в явном
виде:
![]() . (5.2)
. (5.2)
Про уравнение (5.2) говорят, что оно разрешено
относительно ![]() -й производной.
-й производной.
Определение. Порядком уравнения называется порядок старшей производной, входящей в это уравнение.
Определение.
Решением уравнения (5.1) называется такая функция ![]() , которая, будучи подставленной, в
уравнение, обращает его в тождество.
, которая, будучи подставленной, в
уравнение, обращает его в тождество.
Определение.
Если ![]() - решение дифференциального
уравнения, то кривая
- решение дифференциального
уравнения, то кривая ![]() называется интегральной
кривой этого уравнения.
называется интегральной
кривой этого уравнения.
Пример. ![]() . Это уравнение первого порядка,
разрешенное относительно производной. Его решение есть функция
. Это уравнение первого порядка,
разрешенное относительно производной. Его решение есть функция ![]() . Это легко проверяется подстановкой
функции в уравнение. Интегральной кривой является кривая
. Это легко проверяется подстановкой
функции в уравнение. Интегральной кривой является кривая ![]() . При разных значениях
. При разных значениях ![]() получаем разные интегральные кривые.
получаем разные интегральные кривые.
Из формул (5.1) и (5.2) получаем, что обыкновенное дифференциальное уравнение первого порядка имеет вид
![]() (5.3)
(5.3)
или
![]() . (5.4)
. (5.4)
Общее решение дифференциального уравнения (5.3) или (5.4) имеет вид
![]() , (5.5)
, (5.5)
где ![]() - произвольная постоянная.
- произвольная постоянная.
Если в (5.5) вместо ![]() подставить
определенное значение
подставить
определенное значение ![]() , то получим частное
решение уравнения:
, то получим частное
решение уравнения:
![]() . (5.6)
. (5.6)
Не всегда решение можно записать в явном виде (5.5). Часто получаем решение, записанное следующим образом:
![]() , (5.7)
, (5.7)
которое не разрешено
относительно ![]() . Разрешив его относительно
. Разрешив его относительно ![]() , если это возможно, получим общее
решение (5.5).
, если это возможно, получим общее
решение (5.5).
Равенство (5.7), задающее общее решение неявно, называется общим интегралом
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.