Определение
1. Пусть ![]() непрерывна
на интервале
непрерывна
на интервале ![]() . Если существует предел
. Если существует предел
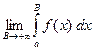 , (3.1)
, (3.1)
то его называют несобственным интегралом
первого рода от функции ![]() на интервале
на интервале ![]() и обозначают следующим образом
и обозначают следующим образом
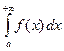 . (3.2)
. (3.2)
Таким образом,
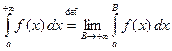 . (3.3)
. (3.3)
При этом, если предел (3.1) конечен, то говорят, что интеграл (3.2) сходится. Если предел (3.1) не существует или бесконечен, то говорят, что интеграл (3.2) расходится. Если интеграл сходится, то говорят также, что он существует, и если он расходится, то говорят, что он не существует.
Аналогично
определяются интегралы на интервале ![]() и на интервале
и на интервале ![]() :
:
![]() , (3.4)
, (3.4)
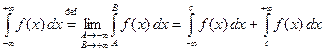 . (3.5)
. (3.5)
Интеграл слева в (3.5) сходится, если сходятся оба интеграла в правой части.
Пример.
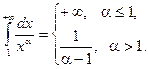 .
.
Таким образом,
интеграл расходится при ![]() и сходится при
и сходится при ![]() .
.
|
|
Если ![]() на
на ![]() , то
, то 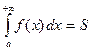 , где
, где ![]() - площадь неограниченной
области, заключенной между кривыми
- площадь неограниченной
области, заключенной между кривыми ![]()
![]() и
и ![]() .
.
Определение
2. Пусть функция ![]() непрерывна
на интервале
непрерывна
на интервале ![]() , а в точке
, а в точке ![]() либо
не определена, либо терпит разрыв. Точка
либо
не определена, либо терпит разрыв. Точка ![]() называется
особой точкой функции
называется
особой точкой функции ![]() . Если существует
предел
. Если существует
предел
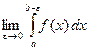 , (3.6)
, (3.6)
то его называют несобственным интегралом
второго рода от функции ![]() на отрезке
на отрезке ![]() и обозначают следующим образом
и обозначают следующим образом
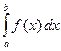 . (3.7)
. (3.7)
Таким образом,
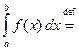
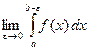 . (3.8)
. (3.8)
Если предел (3.6) конечен, то интеграл (3.7) называют сходящимся, в противном случае - расходящимся.
Аналогично
определяется интеграл от ![]() на отрезке
на отрезке ![]() , если
, если ![]() -
особая точка:
-
особая точка:
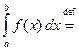
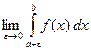 . (3.9)
. (3.9)
Если ![]() и
и ![]() -
особые точки, то
-
особые точки, то
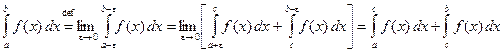 , (3.10)
, (3.10)
где ![]() . Интеграл в левой
части (3.10) сходится тогда и только тогда, когда сходятся оба интеграла в
правой части (оба предела конечны).
. Интеграл в левой
части (3.10) сходится тогда и только тогда, когда сходятся оба интеграла в
правой части (оба предела конечны).
Пусть ![]() - особая точка (
- особая точка (![]() ),
тогда
),
тогда
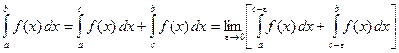 . (3.11)
. (3.11)
Интеграл слева сходится, если сходится каждый из интегралов в правой части.
Пусть функция ![]() непрерывна, например, в промежутке
непрерывна, например, в промежутке ![]() . Тогда по определению
несобственного интеграла первого рода и по формуле Ньютона-Лейбница
. Тогда по определению
несобственного интеграла первого рода и по формуле Ньютона-Лейбница
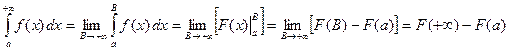 , где
, где ![]() -
первообразная функции
-
первообразная функции ![]() ,
, ![]() .
.
Пусть функция
непрерывна на ![]() ,
, ![]() -
особая точки функции. Тогда
-
особая точки функции. Тогда
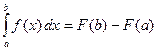 , где
, где ![]() .
.
Пример. 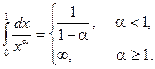
С помощью формулы Ньютона-Лейбница для несобственных интегралов можно доказать свойства, аналогичные свойствам 1-3 определенных интегралов. Также можно доказать формулу интегрирования по частям и формулу замены переменной в несобственном интеграле.
Задание. Сформулировать свойства и доказать любое из них. Сформулировать формулу интегрирования по частям и формулу замены переменной.
Признак
сходимости. Пусть ![]() -
особая точка функции
-
особая точка функции ![]() или
или ![]() .
Пусть функция
.
Пусть функция ![]()
![]() .
Тогда для сходимости несобственного интеграла
.
Тогда для сходимости несобственного интеграла 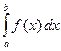 необходимо
и достаточно, чтобы существовала такая константа
необходимо
и достаточно, чтобы существовала такая константа ![]() , что
для всех
, что
для всех ![]() выполнялось бы неравенство
выполнялось бы неравенство 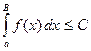 .
.
Аналогичный
признак можно сформулировать для случая, когда ![]() - особая
точка функции
- особая
точка функции ![]() и когда
и когда ![]() .
.
Первый признак сравнения. Пусть
1. ![]() - особая точка функций
- особая точка функций ![]() ,
, ![]() или
или ![]() .
.
2. ![]() .
.
3. ![]() . (3.12)
. (3.12)
Тогда:
a) если интеграл 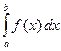 сходится, то
сходится и интеграл
сходится, то
сходится и интеграл 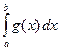 ;
;
b) если
интеграл 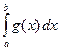 расходится, то расходится и интеграл
расходится, то расходится и интеграл 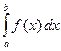 .
.
Второй признак сравнения. Пусть
1.
![]() - особая точка
функций
- особая точка
функций ![]() ,
, ![]() или
или
![]() .
.
2.
![]()
![]() .
.
3. Существует предел
![]() . (3.13)
. (3.13)
Тогда:
a)
если интеграл 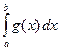 сходится
и
сходится
и ![]() , то сходится интеграл
, то сходится интеграл 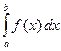 ;
;
b)
если интеграл 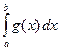 расходится
и
расходится
и ![]() , то расходится интеграл
, то расходится интеграл 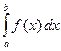 .
.
Следствие. При ![]() интегралы
интегралы 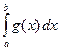 и
и 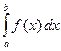 одновременно сходятся или одновременно
расходятся.
одновременно сходятся или одновременно
расходятся.
В частности, если ![]() при
при ![]() , то
интегралы
, то
интегралы 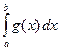 и
и 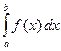 одновременно
сходятся или одновременно расходятся.
одновременно
сходятся или одновременно расходятся.
Аналогичные
признаки сравнения можно сформулировать для случая, когда ![]() - особая точка функции
- особая точка функции ![]() и когда
и когда ![]() .
.
Часто функция ![]() сравнивается с функцией
сравнивается с функцией ![]() , т. к. нам известно, когда сходятся интегралы
, т. к. нам известно, когда сходятся интегралы
![]() и
и ![]() .
.
Определение. Несобственный интеграл 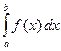 называется абсолютно
сходящимся, если сходится интеграл
называется абсолютно
сходящимся, если сходится интеграл 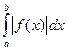 .
.
Из второго признака сравнения следует, что если несобственный интеграл сходится абсолютно, то он сходится.
Примеры.
1.
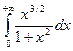 . Подынтегральная
функция
. Подынтегральная
функция ![]() . При
. При ![]()
![]() . Сравним функцию
. Сравним функцию ![]() с функцией
с функцией ![]() . Рассмотрим
. Рассмотрим
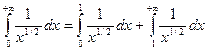 . Так как расходится второй интеграл в
правой части, то расходится и интеграл
. Так как расходится второй интеграл в
правой части, то расходится и интеграл 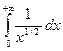 .
Следовательно, по второму признаку сравнения получаем, что исследуемый интеграл
также расходится.
.
Следовательно, по второму признаку сравнения получаем, что исследуемый интеграл
также расходится.
2.
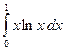 . Так как
. Так как ![]() , то
, то ![]() .
. ![]() сходится. Следовательно, по первому
признаку сравнения сходится и исследуемый интеграл.
сходится. Следовательно, по первому
признаку сравнения сходится и исследуемый интеграл.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.