Интегрирование некоторых тригонометрических функций. Интегрирование с помощью тригонометрических подстановок

1.9.  Интегрирование некоторых тригонометрических функций

Рассмотрим вычисление интегралов вида , где  - некоторая рациональная функция, например, .

a)  Можно сделать универсальную подстановку .

, , , .

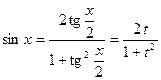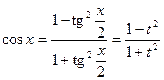По формуле (1.4) получаем:

.

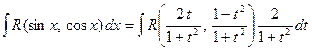b)  Пусть подынтегральная функция нечетная относительно , т.е.  . Например, . В этом случае можно сделать замену . По формуле (1.4):

.

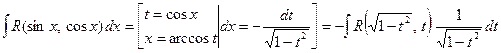c)  Пусть подынтегральная функция нечетная относительно , т.е.  . Например, . Этот интеграл можно вычислить с помощью замены .

.

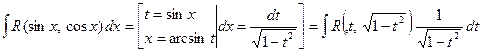d)  Пусть . Например, . В этом случае подойдет замена .

, .                            (1.11)

Тогда

.

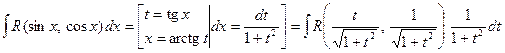e)  .

f)  , .

g)  . Подобные интегралы вычисляются с помощью формул понижения степени: .

h)  . В данном случае применяются тригонометрические формулы:

,

,

.

Примеры.

1)

.

2)  .

1.10.  Интегрирование некоторых иррациональных функций

1) Рассмотрим интеграл вида               

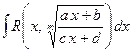,                                                      (1.12)

 - рациональная функция двух аргументов, ,  - постоянные.

Данный интеграл вычисляется с помощью замены 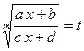. Отсюда .

2) Рассмотрим интегралы вида

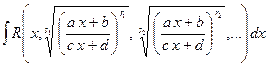.                                     (1.13)

Делается такая же замена, как и в предыдущем случае, но  - общий знаменатель дробей  , ,…

Пример.

.

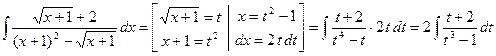Получили интеграл от рациональной функции, который вычисляется методом неопределенных коэффициентов.

1.11.  Интегрирование с помощью тригонометрических подстановок

Рассмотрим интегралы вида

,                                                  (1.14)

где  и .

Выделяя полный квадрат в выражении , сведем интеграл (1.14) к одному из следующих трех видов.

,

,

.

Первый интеграл  вычисляется с помощью замены . По формуле (1.4)  получаем:

.

Второй интеграл  вычисляется с помощью замены :

.

Третий интеграл  вычисляется с помощью замены :

.

Пример.

.

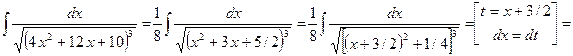
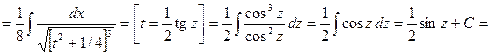
Учитывая вторую из формул (1.11), получаем:

.

1.12.  Подстановки Эйлера

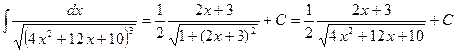Рассмотрим интегралы вида .

Если , то можно делать первую подстановку Эйлера: .

Если , то можно делать вторую подстановку Эйлера .

Если подкоренное выражение имеет вещественные корни: , то можно делать третью подстановку Эйлера: .