расстояние от расчетного сечения до рассмариваемого i-го соседнего с расчетным колеса, см.
Расчет значений кромочных напряжений в подошве рельса от воздействия на путь обращающихся по рассматриваемому участку типов подвижного состава выполнен в табличной форме. Результаты расчета сведены в таблицу 1.3.
Согласно таблице 1.3 наибольшие кромочные напряжения в подошве рельса______________, возникают от воздействия на путь тепловоза 2ТЭ10В и их величина не превышает допускаемой величины напряжений в рельсах стандартного производства, величина которой [ р]=4000кгс/см2. Таким образом,для дальнейшего расчета рассматриваемого участка пути на прочность и устойчивость, в качестве расчетного экипажа принимается тепловоз 2ТЭ10В, обращающийся по рассматриваемому участку со скоростью до 100 км/ч.
Таблица 1.3 – Расчет кромочных напряжений в подощве рельса от подвижного состава
|
Тип экипажа |
Рсm, кгс |
Рр, кгс |
0,75Рр, кгс |
Рср=Рсm+0,75Рр, кгс |
Sнп, кгс |
mРср, кгс |
Р¢экв, кгс |
sкг, кгс/см2 |
|
ТЭП60 |
10750 |
1881 |
1411 |
12161 |
для |
лета |
||
|
2870 |
-1148 |
18474 |
997 |
|||||
|
для |
зимы |
|||||||
|
3722 |
-557 |
21280 |
992 |
|||||
|
2ТЭ10В |
11500 |
2790 |
2093 |
13593 |
для |
лета |
||
|
4124 |
-2008 |
22307 |
1314 |
|||||
|
для |
зимы |
|||||||
|
5348 |
-1262 |
26230 |
1299 |
|||||
|
Четырехосный грузовой вагон |
10500 |
5200 |
3900 |
14400 |
для |
лета |
||
|
2323 |
-2236 |
18204 |
1055 |
|||||
|
для |
зимы |
|||||||
|
3012 |
-1446 |
20785 |
1012 |
|||||
|
Шестиосный грузовой вагон |
10700 |
4290 |
3218 |
13918 |
для |
лета |
||
|
2352 |
-2248 |
16374 |
908 |
|||||
|
для |
зимы |
|||||||
|
3050 |
-1535 |
18483 |
862 |
|||||
|
Восьмиосный грузовой вагон |
10550 |
3800 |
2850 |
13400 |
для |
лета |
||
|
2161 |
-2092 |
16927 |
981 |
|||||
|
для |
зимы |
|||||||
|
2803 |
-1226 |
19462 |
948 |
|||||
1.2.4 Детальный расчет пути на прочность
Задачей детального расчета пути на прочность является определение допустимости обращения рассматриваемой единицы подвижного состава (расчетного экипажа) по заданному участку пути, и если это допустимо, то с какой наибольшей скоростью возможно обращение. Согласно расчетам, выполненным в п.1.2.3 за расчетный экипаж принят тепловоз 2ТЭ10В.
Динамический расчет пути под воздействием системы грузов, действующих на путь от колес экипажа, сводится к тому, чтобы найти такую эквивалентную силу, которая, будучи статически приложена в расчетном сечении, по своему воздействию на путь оказалось бы эквивалентной динамическому воздействию на это сечение пути всей системы грузов.
эквивалентные силы определяются по следующим формулам:
Где Рср – среднее значение вертикальных сил от расчетного колеса, состоящего из статической нагрузки и среднего дополнительного давления от колебания рессор, кгс; определяется по формуле (1.4);
lф - нормирующий множитель, приводящий значение Рэкв к заданному уровню вероятности не превышения Ф=0,994; принимается lф=2,5;
S - среднее квадратическое отклонение вертикальных сил, кгс;
Рср+lфS – максимальное давление на рельс от расчетного колеса, кгс;
SРсрm и SРсрh - влияние давления соседних колес, отстоящих от расчетной оси не далее 3,5 м (среднее значение по каждому колесу), соответственно на величину изгибающего момента Мдин и давления Qдин, под расчетным колесом: определяются по следующим формулам
В формуле (1.10) коэффициент относительной жесткости подрельсового основания и рельса соответственно для лета Кл, см-1,
И для зимы Кз, см-1, определяется по формуле (1.2).
В формуле (1.9) среднее квадратическое отклонение вертикальных сил S, кгс, определяется по формуле
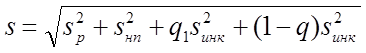 |
,
Где Sр – среднее квадратическое отклонение вертикальных сил, вызываемое колебаниями рессор, кгс;
Sнп – среднее квадратическое отклонение вертикальной силы, вызываемое неровностями на пути, определяется по формуле (1.7), кгс;
q1 - доля колес в поезде, имеющих изолированные неровности, в виду отсутствия фактических эксплуатационных данных по [15, стр8] принимается q1=0,05;
Sинк и Sинк,- среднее квадратическое отклонение давления колеса на рельс, обусловленное силами инерции неподрессоренных масс, возникающих соответственно при наличии изолированной неровности на колесе и при наличии непрерывных главных неровностей на колесах, кгс.
Где Рр - максимальное значение вертикальных сил, вызываемых колебаниями рессор, кгс, определяется по формуле (1.5).
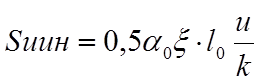 |
,
Где aо=0,403 для пути с железобетонными шпалами [ 15, стр. 8, формула(2,7)];
x- максимальный дополнительный прогиб рельса при прохождении колесом косинусоидальной неровности ,принимается исходя из сопостовления рассматриваемой скорости движения поезда n, км/ч, с критической скоростью nкр,км/ч:
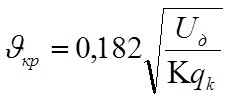 |
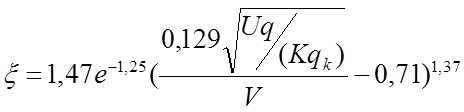 |
Где q- ускорение силы тяжести q=981 см/с2;
eо –величина наибольшей расчётной глубины изолированной неровности на колесе, принимается равной 2/3 от предельно допустимой глубины ползуна и состовляет для колёс локомотивов 0,047 см. прибуксовых подшипников качения.
Среднее квадратическое отклонение Sннк , кгс, в формуле (1.11) определяется по формуле
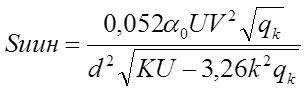 |
Где d- диаметр колеса по кругу катания, согласно[15,стр.36, приложение 1 ] для локомотива 2ТЭ10В d=105 см.
Изгибающий момент Мдин, кгс×см; действующий на рельс в расчётном сечении, и давление на шпалу Qдин, кгс, в расчётном сечении определяется по следующим формулам:
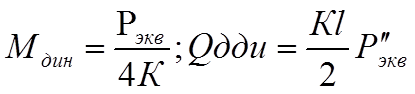 |
Где l- расстояние между осями шпал , см.
Осевые напряжения на нижней постели подошвы рельса sп-о, кгс/см2, и на верхней поверхности головки рельса sг-о , кгс/см2, от изгиба, кромочные напряжения в подошве sп-к, кгс/см2, и головке рельса sг-к, кгс/см2, определяются по формулам:
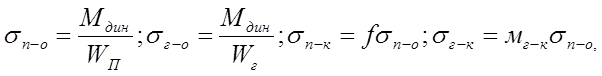
Где Wп и Wг- моменты сопротивления рельсов относительно соответственно подошвы и головки при изгибе в вертикальной плоскости, согласно [15, стр.43, приложение 5] для рельсов типа Р-65
Wп=436см3 и Wг=359см3;
Fи mг-к – соответственно коэффициенты перехода от осевых напряжений к кромочным в подошве и головки рельса, учитывающие горизонтальный изгиб и кручение рельса; на прямом участке пути согласно [15, стр. 44, приложение 6] f=1,260 и [15, стр. 47, приложение 9] mг-к=1,264; на кривой R=800м: f=1,458 и mг-к=1,335.
Средние напряжения в балластном слое под шпалами в подрельсовом сечении sб, кгс/см2, и действующие напряжения под подкладкой в шпалах sш, кгс/см2, определяется по следующим формулам:
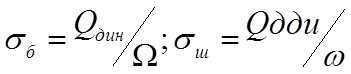 |
Где W- эффективная опрная площадь полушпалы, согласно [15, стр. 48, приложение 10] при щебёночном балласте и железобетонных шпалах
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.