





















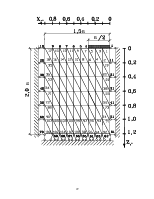



































результатам расчетов были построены графики осадок (рис.2.2,а). При расположении штампа "на слабом" грунте I графики осадок имели криволинейную форму, на грунте II, - в большом диапазоне нагрузок они имели слабую кривизну. Значения осадок, полученных расчетом, превышали установленные по СНиП [102] даже на первых ступенях нагрузки штампа (табл.2.1).
Таблица 2.1
|
Вид основания |
p, кН/м2 |
Перемещения штампа S, м |
|||
|
Программа «Геомеханика» |
Формула Шлейхера |
СНиП [102] |
|||
|
Метод послой-ного суммирования |
Метод сжимаемого слоя |
||||
|
ГРУНТ I |
14 |
0.001 |
0.0006 |
0.0006 |
0.0005 |
|
24 |
0.002 |
0.0010 |
0.0009 |
0.0009 |
|
|
47 |
0.010 |
0.0019 |
0.0018 |
0.0018 |
|
|
ГРУНТ II |
194 |
0.01 |
0.008 |
0.008 |
0.008 |
|
911 |
0.05 |
0.039 |
0.036 |
0.035 |
|
|
1815 |
0.10 |
0.078 |
0.071 |
0.070 |
|
|
5373 |
0.30 |
0.230 |
0.210 |
0.210 |
|
Различие в величине осадок, полученных расчетом при соответствующих исходных данных с применением нелинейной и линейной моделей полуплоскости, есть следствие глубинных процессов протекающих в массиве грунта.
По
результатам счета [112] построены эпюры распределения вертикальных напряжений
и ![]() 1=s1/рср
и
1=s1/рср
и ![]() 3=s3/рср
(p - среднее давление
3=s3/рср
(p - среднее давление
|
по подошве) (рис.2.2,2.3). Здесь же представлены эпюры, построенные по решению теории упругости для жесткого штампа.
Отметим особенности распределения напряжений ![]() 1 и
1 и
![]() 3 на
глубине z=0.17b и z=0.83b (грунт I, II, рис.2.2), полученных по решению теории
упругости и по программе "Геомеханика".
3 на
глубине z=0.17b и z=0.83b (грунт I, II, рис.2.2), полученных по решению теории
упругости и по программе "Геомеханика".
Значения ![]() 1 (грунт
I, рис.2.2,а,"малая" нагрузка) на глубине z=0.17b и 0£х£b/2 больше
установленных по теории упругости; за границей подошвы штампа напряжения
1 (грунт
I, рис.2.2,а,"малая" нагрузка) на глубине z=0.17b и 0£х£b/2 больше
установленных по теории упругости; за границей подошвы штампа напряжения ![]() 1 по
теории упругости превышают установленные нашим расчетом по программе
"Геомеханика"; максимум напряжений
1 по
теории упругости превышают установленные нашим расчетом по программе
"Геомеханика"; максимум напряжений ![]() 1 в
этом случае наблюдается при x=0.42b, с глубиной максимум
1 в
этом случае наблюдается при x=0.42b, с глубиной максимум ![]() 1 смещается
к оси симметрии штампа. Напряжения
1 смещается
к оси симметрии штампа. Напряжения ![]() 3 в
точках центральной вертикали штампа меньше, чем по теории упругости, а на
некотором расстоянии (x>0.25b) наблюдается обратная картина. Эпюра
напряжений
3 в
точках центральной вертикали штампа меньше, чем по теории упругости, а на
некотором расстоянии (x>0.25b) наблюдается обратная картина. Эпюра
напряжений ![]() 3
на этом участке имеет максимум (при х=0.42b).
3
на этом участке имеет максимум (при х=0.42b).
Характер распределения ![]() 1 (грунт
II, рис.2.2,а, "малая" нагрузка) на глубине z=0.17b соответствует
таковому для грунта I для этой же глубины. Эпюры
1 (грунт
II, рис.2.2,а, "малая" нагрузка) на глубине z=0.17b соответствует
таковому для грунта I для этой же глубины. Эпюры ![]() 3 в
решении нелинейной задачи повторяют очертания эпюр
3 в
решении нелинейной задачи повторяют очертания эпюр ![]() 3 по
теории упругости, однако величина их ординат в первом случае меньше, чем во
втором (участок 0<x£0.58b).
3 по
теории упругости, однако величина их ординат в первом случае меньше, чем во
втором (участок 0<x£0.58b).
Напряжения ![]() 1 и
1 и
![]() 3 (грунт
I, II, рис.2.2,а, "малая" нагрузка) на глубине z=0.83b распределены
так же, как на глубине z=0.17b, а
3 (грунт
I, II, рис.2.2,а, "малая" нагрузка) на глубине z=0.83b распределены
так же, как на глубине z=0.17b, а ![]() 3,
полученные по программе "Геомеханика", в любой точке на данной глубине
превышают значения
3,
полученные по программе "Геомеханика", в любой точке на данной глубине
превышают значения ![]() 3,
установленные по теории упругости.
3,
установленные по теории упругости.
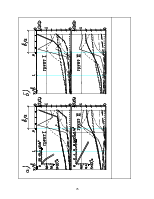
Сравнивая
эпюры ![]() 1
и
1
и ![]() 3
(грунт I, II, рис.2.2,б) при "малой" и "большой"
нагрузке, можно отметить, что их поведение аналогично описанному выше (грунт I,
II, рис.2.2,а) при этих же условиях.
3
(грунт I, II, рис.2.2,б) при "малой" и "большой"
нагрузке, можно отметить, что их поведение аналогично описанному выше (грунт I,
II, рис.2.2,а) при этих же условиях.
Сопоставим
распределение напряжений ![]() 1 и
1 и
![]() 3 (грунт
I, II, рис.2.3) вдоль центральной и угловой вертикалей, полученных по решению
теории упругости и по программе "Геомеханика".
3 (грунт
I, II, рис.2.3) вдоль центральной и угловой вертикалей, полученных по решению
теории упругости и по программе "Геомеханика".
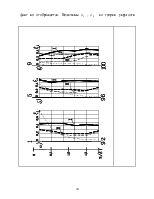
Распределение
вертикальных напряжений ![]() 1 и
1 и
![]() 3 (грунт
I, рис. 2.3,а-б, "Геомеханика") вдоль центральной вертикали штампа,
свидетельствует о концентрации напряжений с появлением максимума их на глубине
z=0.83b. Значения напряжений
3 (грунт
I, рис. 2.3,а-б, "Геомеханика") вдоль центральной вертикали штампа,
свидетельствует о концентрации напряжений с появлением максимума их на глубине
z=0.83b. Значения напряжений ![]() 1 и
1 и
![]() 3 при
S=0.02b и 0.03b, несколько различаются, что соответствует экспериментальным
данным [65], а в решениях теории упругости этот факт не отображается. Величины
3 при
S=0.02b и 0.03b, несколько различаются, что соответствует экспериментальным
данным [65], а в решениях теории упругости этот факт не отображается. Величины
![]() 1 ,
1 ,
![]() 3 по
теории упругости
3 по
теории упругости
|
|
значительно меньше, чем полученные
по нашему расчету. Лишь под подошвой штампа ![]() 3 по
теории упругости несколько больше наших расчетных значений.
3 по
теории упругости несколько больше наших расчетных значений.
Наибольшие
значения ![]() 1
и
1
и ![]() 3
(грунт I, рис. 2.3,а-б) для угловой вертикали как по теории упругости,
так и по расчету ("Геомеханика") получаются под подошвой штампа,
причем на глубине z=(0.33..0.83)b по расчету наблюдаются уменьшенные
напряжения. Напряжения
3
(грунт I, рис. 2.3,а-б) для угловой вертикали как по теории упругости,
так и по расчету ("Геомеханика") получаются под подошвой штампа,
причем на глубине z=(0.33..0.83)b по расчету наблюдаются уменьшенные
напряжения. Напряжения ![]() 3 имеют
эпюры, аналогичные эпюрам
3 имеют
эпюры, аналогичные эпюрам ![]() 1.
Напряжения
1.
Напряжения ![]() 3
при перемещениях S=0.02b превышают значения, полученные по теории
упругости до глубины z=0.33b, затем их значения совпадают или отличаются
незначительно. Во всех остальных случаях напряжения
3
при перемещениях S=0.02b превышают значения, полученные по теории
упругости до глубины z=0.33b, затем их значения совпадают или отличаются
незначительно. Во всех остальных случаях напряжения ![]() 1 и
1 и
![]() 3 больше
установленных по теории упругости; и лишь на глубинах z=(0.33..0.83)b
наблюдается обратное явление.
3 больше
установленных по теории упругости; и лишь на глубинах z=(0.33..0.83)b
наблюдается обратное явление.
Эпюры,
полученные по решению нелинейной задачи (грунт II, рис. 2.3,а-б) вдоль
центральной и угловой вертикалей, имеют увеличенные значения ординат по
сравнению с данными теории упругости, это объясняется появлением зон сдвигов у
граней штампа. Максимума напряжений ![]() 1 и
1 и
![]() 3 по
вертикальным направлениям не наблюдается; с возрастанием глубины расположения
точки, напряжения плавно уменьшаются при любом значении перемещений штампа.
Напряжения
3 по
вертикальным направлениям не наблюдается; с возрастанием глубины расположения
точки, напряжения плавно уменьшаются при любом значении перемещений штампа.
Напряжения ![]() 3
под подошвой штампа по решению нелинейной задачи для центральной и угловой
вертикалей меньше, чем по теории упругости, но уже с глубины z=0.17b напряжения
3
под подошвой штампа по решению нелинейной задачи для центральной и угловой
вертикалей меньше, чем по теории упругости, но уже с глубины z=0.17b напряжения
![]() 3 превышают
значения, установленные решением теории
3 превышают
значения, установленные решением теории
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.