
Рассмотрим задачу Коши:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() .Тогда
из общего решения уравнения выделяется частное решение
.Тогда
из общего решения уравнения выделяется частное решение ![]() , которгое и возьмем в
качестве тестового.
, которгое и возьмем в
качестве тестового.
Получим численное решение задачи Коши в узлах![]() ,
, ![]() ,
, ![]() , где
, где ![]() - задаваемый параметр. В
моем варианте( вариант №14) предлагались следущие расчетные формулы, с
различной погрешностью на всем интервале
- задаваемый параметр. В
моем варианте( вариант №14) предлагались следущие расчетные формулы, с
различной погрешностью на всем интервале ![]() :
:
a) ![]() ,
(формула Эйлера) ,
,
(формула Эйлера) ,![]()
с) ![]() ,
, ![]() ,
, ![]() ,
,![]()
f) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
В задании необходимо получить численное решение задачи Коши, используя предложенные расчетные формулы. Вывести
1) норму невязки в ![]() для различного числа
разбиений
для различного числа
разбиений ![]() (
(![]() ) отрезка; 2) порядок
сходимости
) отрезка; 2) порядок
сходимости ![]() предложенных численных
методов;
предложенных численных
методов;
3) константу аппроксимации ![]() .
.
![]() .
.
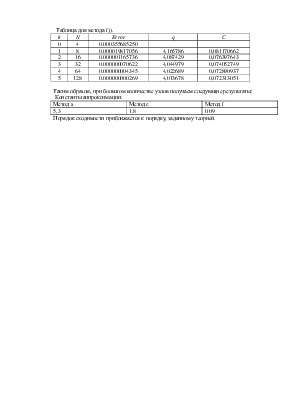
Таблица для метода а).
|
k |
N |
Error |
q |
C |
|
0 |
4 |
1.080880713 |
||
|
1 |
8 |
0.594203014 |
0.750972 |
4,753684111 |
|
2 |
16 |
0.313193222 |
0.923902 |
5,011091544 |
|
3 |
32 |
0.161015459 |
0.959253 |
5,152494701 |
|
4 |
64 |
0.081666882 |
0.979376 |
5,226680451 |
|
5 |
128 |
0.041130379 |
0.989546 |
5,264688450 |
Таблица для метода с).
|
k |
N |
Error |
q |
C |
|
0 |
4 |
0.094315511 |
||
|
1 |
8 |
0.025316604 |
1.897411 |
1,620262647 |
|
2 |
16 |
0.006599429 |
1.939670 |
1,689453943 |
|
3 |
32 |
0.001686988 |
1.967891 |
1,727475908 |
|
4 |
64 |
0.000426597 |
1.983503 |
1,747341600 |
|
5 |
128 |
0.000107269 |
1.991640 |
1,757487401 |
Таблица для метода f)).
|
k |
N |
Error |
q |
C |
|
0 |
4 |
0.000355685250 |
||
|
1 |
8 |
0.000019817056 |
4,165786 |
0,081170662 |
|
2 |
16 |
0.000001165736 |
4,087429 |
0,076397643 |
|
3 |
32 |
0.000000070622 |
4,044979 |
0,074052749 |
|
4 |
64 |
0.000000004345 |
4,022689 |
0,072890937 |
|
5 |
128 |
0.000000000269 |
4,013678 |
0,072313051 |
Таким образом, при большом количестве узлов получаем следующие результаты:
Константы аппроксимации:
|
Метод a |
Метод с |
Метод f |
|
5,3 |
1.8 |
0.09 |
Порядок сходимости приближается к порядку, заданному теорией.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.