Решение уравнения теплопроводности. Двухслойная разностная схема

1. Описание постановки задачи.

Рассмотрим задачу о распространении тепла в стержне, теплоизолированном по «поверхности», на концах которого выполняются различные условия теплообмена:

, , .                                    

Граничные и начальные условия:

При  ;      

При  ,          при  .                                                       

Здесь  - заданная правая часть, ,  - линейные дифференциальные выражения, ,  - заданные параметры, либо заданные асимптотически постоянные функции  (температура окружающей среды),   - заданная функция (начальное распределение температуры в стержне).

2.Тестовое решение.

В предыдущем отчете подробное описывалось построение тестового решения для уравнения теплопроводности, которое в конечном итоге имеет вид :

.

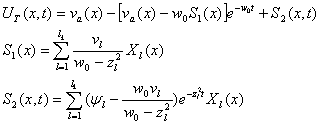Граничные условия нестационарны, правой части нет:

, , ,

И

где , (),  - финитная функция в виде равнобедренного треугольника с высотой , вершиной в точке и шириной полуоснования .

3.Разностное уравнение, разностные граничные условия.

Введем в области решения задачи  равномерную сетку  (),  (), где , , где  - фиксированный параметр разностной задачи.

Разностные решения на сетке обозначим:

.

Производную  в граничных условиях можно аппроксимировать разностными выражениями с различным порядком. Мне предлагались следующие варианты аппроксимации:

а) ,  - приближение первого порядка.

в) ,  - приближение второго порядка, не выводящее за пределы области.

Граничные условия  , аппроксимируем разностными выражениями, полученными с использованием формул а и в.

Разностные граничные условия имеют вид:

а) , .

в) , .

4. Двухслойная разностная схема.

Нашему уравнению поставим в соответствие разностное уравнение:

;  - весовой параметр схемы, . При  схема явная, при  - неявная.

Преобразуем разностное уравнение  к виду:

                                                                        где в  собраны все выражения на k-м слое.

Получаем:

.

.

.

Уравнение  удобно решать по методу прогонки:

,                                                                         

,                                                                     где .

Если известны , то по формулам все  находятся рекуррентно, затем, если известно , то все находятся.

Для нахождения ,,следует привлечь граничные условия: а) .

Преобразуя, получаем:  , .

При :

. Получаем систему для нахождения :

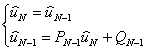.Таким образом, .

Метод в).

При :

Имеем .

получаем систему:

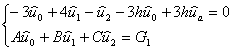.Преобразуя, получаем:

, .При :

,

При :

получаем систему для нахождения :

.

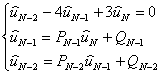Таким образом:

.

5. Полученные результаты.

Все расчеты произведены для ,,,, , ,

Таблица для метода a)

Таблица для метода в)

По данным из таблицы можно сделать вывод, что порядок сходимости соответствует заявленному теоретически, а именно:

Для метода а  - первый порядок сходимости

Для метода в – второй.