Пусть в области ![]() дано
уравнение
дано
уравнение
![]() с граничными условиями смешанного типа
с граничными условиями смешанного типа
![]() (при
(при ![]() )
)
![]() (при
(при ![]() ) где
) где ![]() ,
, ![]() - заданный параметр.
- заданный параметр.
В уравнении ![]() и
и
![]()
где ![]() -
известное (заданное) тестовое решение.
-
известное (заданное) тестовое решение.
Введем в области ![]() равномерную
сетку с узлами
равномерную
сетку с узлами ![]() ,
, ![]() ,
, ![]() , где
, где ![]() - заданный параметр.
- заданный параметр.
Аппроксимируем вторую производную с порядком ![]() :
:
![]() где введены сеточные функции
где введены сеточные функции ![]() ,
, ![]() .
.
Тогда уравнению![]() будет соответствовать разностное уравнение вида
будет соответствовать разностное уравнение вида
![]()
Найдем ![]() методом
подстановки выражения для второй производной в наше уравнение:
методом
подстановки выражения для второй производной в наше уравнение:
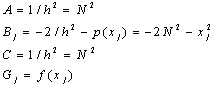 .
.
Разностное уравнение эффективно решается с помощью метода прогонки:
![]() ,
, ![]() , где
, где ![]() выражаются
через
выражаются
через ![]() по формулам
по формулам
![]() ,
, ![]() .
.
Чтобы
воспользоваться формулой для прогонки нужно получить ![]() ,
, ![]() , для чего привлекается
граничное условие
, для чего привлекается
граничное условие ![]() .Для счета
.Для счета ![]() по прогоночной
формуле необходимо, кроме сосчитанных
по прогоночной
формуле необходимо, кроме сосчитанных ![]() ,
,
![]() , иметь значение
, иметь значение ![]() , которое находится с
помощью граничного условия
, которое находится с
помощью граничного условия ![]() .
.
.
Аппроксимация первой производной в граничных условиях при реализации последних.
а).
При ![]() :
:
![]() - грубое приближение
первого порядка, снижающее точность расчетов.
- грубое приближение
первого порядка, снижающее точность расчетов.
Подставим в граничное условие ![]() . Получим:
. Получим: ![]() .
.
В результате имеем: ![]() ,
, ![]() .
.
При ![]() :
:
![]() - приближение первого
порядка.
- приближение первого
порядка.
Подставим в граничное условие![]() и используя (7):
и используя (7): ![]() , находим:
, находим:
![]() .
.
в).
При ![]() :
:
![]() -
аппроксимация второго порядка, не требующая выхода за пределы единичного
интервала.
-
аппроксимация второго порядка, не требующая выхода за пределы единичного
интервала.
Подставим в граничное условие ![]() и используя
и используя
![]() ,
находим:
,
находим: ![]() .
.
Таким образом получаем 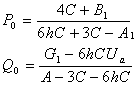 .
.
При x=1:
![]() -
приближение второго порядка..
-
приближение второго порядка..
Подставим в граничное условие ![]() . Решая систему:
. Решая систему:
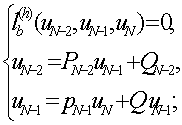 ,
находим
,
находим
![]() .
.
Возьмем две гладкие функции ![]() и
и ![]() , сконструируем тестовое
решение в виде:
, сконструируем тестовое
решение в виде:
![]() , где
, где ![]() зададим как параметр, а
зададим как параметр, а ![]() и
и ![]() найдем из граничных
условий (2) и (3), которые дадут систему:
найдем из граничных
условий (2) и (3), которые дадут систему:
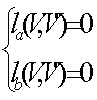 , или в
нашем случае:
, или в
нашем случае:
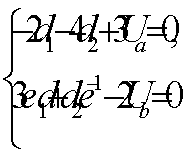
Решая систему, находим коэффициенты :
![]() ,
, ![]()
Расчеты произведены для ![]() ,
, ![]() ,
, ![]() .
.
![]()
![]() .
.
Метода а.
|
k |
N(число узлов) |
Error(погрешность) |
q(порядок сходимости) |
|
0 |
4 |
0,67414432 |
0,41807099 |
|
1 |
8 |
0,50454624 |
0,84103825 |
|
2 |
16 |
0,28165874 |
0,93633434 |
|
3 |
32 |
0,14718329 |
0,97046390 |
|
4 |
64 |
0,07511381 |
0,98564829 |
|
5 |
128 |
0,3793238 |
0,99289734 |
|
6 |
256 |
0,01905979 |
Таблица 2(для метода б)).
|
k |
N |
Error |
q |
|
0 |
4 |
1,27191275 |
0,81842653 |
|
1 |
8 |
0,72125093 |
2,13036613 |
|
2 |
16 |
0,16473363 |
2,28304321 |
|
3 |
32 |
0,03370634 |
2,2326053 |
|
4 |
64 |
0,00717176 |
2,14771325 |
|
5 |
128 |
0,00161845 |
2,08246651 |
|
6 |
256 |
0,00038213 |
Таким образом, по данным таблицы можно сделать вывод, что метод а имеет первый порядок сходимости, метод в имеет второй порядок сходимости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.