Интегрирование функций одной переменной. Метод статистических испытаний (метод Монте-Карло)

ЗАДАНИЕ № 3

Интегрирование функций одной переменной

Вычисление определенных интегралов с помощью численных методов сводится к построению т.н. квадратурных формул.

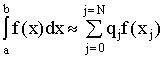,                                                          (1)

где - непрерывная на [a,b] функция,  - веса и узлы квадратурной формулы, причем . Достаточно общий подход к построению квадратурных формул заключается в разбиении отрезка интегрирования [a,b] на N интервалов  в общем случае переменной длины и в замене на каждом из них подинтегральной функции  какой-либо близкой к ней функцией , интеграл от которой вычисляется аналитически. После этого, используя свойство аддитивности,  интеграл на всем отрезке [a,b]  вычисляется как сумма интегралов по всем этим интервалам. Очевидно, что погрешность построенной таким образом квадратурной формулы будет тем меньше, чем больше используется число интервалов N и чем точнее функция приближает подинтегральную функцию .

Рассмотрим ряд наиболее употребительных формул численного интегрирования, основанных на этом подходе, полагая для простоты, что отрезок   разбивается на N равных интервалов длины h, где .

1. Формулы прямоугольников

Полагая на каждом из интервалов  подинтегральную функцию постоянной (на всем отрезке интегрирования она будет кусочно-постоянной), можно построить три варианта квадратурной формулы, называемых формулами прямоугольников. Если , то полагая  или  получаем в первом случае (первая формула прямоугольников)

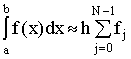,                                                          (2)

где . Погрешность такой формулы  или

Во втором случае (вторая формула прямоугольников)

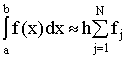.                                                       (3)

Погрешность формулы (3)  т.е. так же

Если же , то полагая , получаем третью формулу прямоугольников

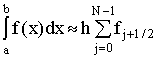                                                    (4)

где . Погрешность такой формулы будет уже  или , т.е. формула (4) будет иметь уже второй порядок точности.

2. Формула трапеций

Заменяя на интервале  подинтегральную функцию прямой, проходящей через две точки, получим формулу трапеций. При этом необходимо, чтобы .

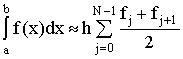                                                         (5)

Формула имеет погрешность  или , т.е. также имеет второй порядок точности.

3. Формула Симпсона

Если отрезок [a,b] разбить на четное число интервалов и объединить каждые два соседних интервала, то на объединенном интервале длиной 2h через каждые три точки  можно провести параболу (полином второй степени), которой и заменяется подинтегральная функция. Если при этом  , то получается квадратурная формула

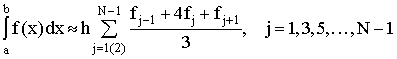,              (6)

Погрешность формулы  или , т.е. имеет уже четвертый порядок точности.

4. Формула Гаусса

Эта квадратурная формула строится следующим образом. После разбиения отрезка интегрирования [a,b] на N интервалов , на каждом из них выбирается n точек  из условий, чтобы приближенная формула 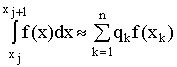  была точной на мономах степени

2n-1. При этом определяются значения как весов , так и абсциссы расположения точек , зависящие от числа n.

Приведем несколько значений этих величин для «стандартного» интервала [-1,1] для ряда значений   n.

n
1	= 0	=1
2	=-0.5773502692; =0.5773502692	=1; =1;
3	= -0.7745966692; =0; = 0.7745966692;	= 0.5555555556; =0.8888888889;=0.5555555556;
4	= -0.8611363116; = -0.3399810436; = 0.3399810436;   = 0.8611363116;	= 0.3478548451; =0.6521451549; =  0.6521451549; =0.3478548451

Тогда на каждом интервале  расположение узлов оказывается следующим:

, где - узлы «стандартного» интервала, значения которых выбираются из таблицы. Тогда

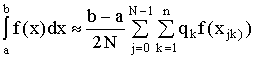.                          (7)

Погрешность формулы 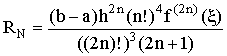, т.е. имеет порядок . Нетрудно видеть, что при n=1 формула (7) совпадает с третьей формулой прямоугольников (4), а при n=2 имеет тот же порядок точности, что и формула Симпсона (6). Поэтому квадратурную формулу (7) целесообразно использовать при n>2.

5. Метод Монте-Карло

Метод статистических испытаний (метод Монте-Карло) основан на использовании серии N  независимых испытаний равномерно распределенной на отрезке [a,b] случайной величины . Приближенное значение интеграла определяется по формуле

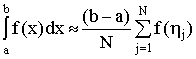                                                  (8)

где - независимые реализации случайной величины . Метод не предъявляет к подинтегральной функции никаких требований гладкости и особенно эффективен при вычислении кратных интегралов. При достаточно большом значении N (N >100) с вероятностью 0.997 выполняется неравнство

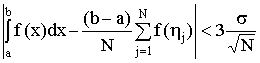,                                    (9)

которое и может служить оценкой точности вычислений. Здесь  есть дисперсия, приближенное значение которой можно вычислять по формуле

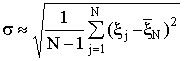  , где .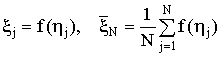

Для получения величины  используйте формулу , где  - равномерно распределенная на [0,1] случайная величина.

6. Практическая оценка точности формул

численного интегрирования (метод Рунге)

Пусть точное значение интеграла  представимо в виде , где - его приближенное значение, вычисленное по какой-либо квадратурной формуле с шагом h, C – неизвестная константа, не зависящая от шага h, и k, m>0 – известные числа. Тогда с точностью до величин порядка имеет место оценка

                                                (10)

где  значение интеграла, полученное по той же самой квадратурной формуле с шагом h/2. Эту же оценку точности можно использовать для получения уточненного (более точного чем ) значения интеграла

                                (11)

Значения величины k есть порядок точности квадратурной формулы, полученный теоретическим путем. Так, k=1 для формул (2, 3), k=2 для формул (4, 5), k=4 для формулы Симпсона (6) и k=2n для формулы Гаусса (7).

Задание

1.  С помощью всех рассмотренных выше формул численного интегрирования (2-8) вычислите интеграл 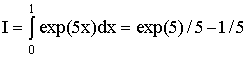  при различных значениях числа интервалов N=10, 20, 40, 80 и числа статистических испытаний N= 10, 100, 1000, 10000 для формулы (8). Для формулы Гаусса выберите два значения величины n:  n = 3 и n = 4 (два варианта формулы Гаусса). В программе описывайте все формулы численного интегрирования в виде функций с единственным формальным параметром N, что позволит легко вычислять интегралы  и . Вычислите реальную точность  и приближенное значение погрешности, полученное по формуле (10) для квадратурных формул и по формуле (9) для метода Монте-Карло (для генерации равномерно распределенной на [0,1] случайной величины  используйте функцию random (обязательно вставьте в начале программы вызов процедуры randomize) . Результаты расчетов выведите на экран в виде таблицы (первый столбец – значения числа N). Проверьте, соответствует ли характер поведения реальной погрешности ее теоретической оценке (как ), а также  убедитесь в близости приближенной оценки погрешности (10, 9) к ее реальному значению.

2.  Проведите аналогичный цикл исследований для интеграла от «разрывной» функции

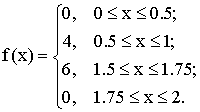
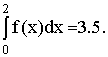       Объясните полученные результаты.

3.  Напишите общий отчет по всей теме.