Рассмотрим задачу о распространении тепла в стержне, теплоизолированном по «поверхности», на концах которого выполняются различные условия теплообмена:
![]() ,
,
![]() ,
,
![]() .
.
Граничные и начальные условия:
При![]()
![]() ;
;
При ![]()
![]() , при
, при ![]()
![]() .
.
Здесь ![]() -
заданная правая часть,
-
заданная правая часть, ![]() ,
,
![]() -
линейные дифференциальные выражения,
-
линейные дифференциальные выражения, ![]() ,
,
![]() -
заданные параметры, либо заданные асимптотически постоянные функции
-
заданные параметры, либо заданные асимптотически постоянные функции ![]() (температура
окружающей среды),
(температура
окружающей среды), ![]() -
заданная функция (начальное распределение температуры в стержне).
-
заданная функция (начальное распределение температуры в стержне).
Если ![]() и
и
![]() ,
то
,
то ![]() ,
то есть к «асимптотическому» решению уравнения теплопроводности. Очевидно, оно
линейно и его можно записать в виде
,
то есть к «асимптотическому» решению уравнения теплопроводности. Очевидно, оно
линейно и его можно записать в виде
![]() , где
, где ![]() ,
,
![]() находятся
из условия удовлетворения
находятся
из условия удовлетворения ![]() граничным
условиям
граничным
условиям ![]() ,
,
![]() .
.
В сформулированной для меня задачи получаем:
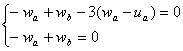 .
.
Таким образом,![]() .
.
Сначала рассмотрим вспомогательную задачу
![]() ;
;
![]() ,
,
![]() ;
;
![]() , где функция
, где функция ![]() позже
будет конкретизирована.
позже
будет конкретизирована.
Решение этой задачи ищем в виде ряда
![]() ;
;
![]() ;
;
![]() .
.
![]() удовлетворяет
уравнению
удовлетворяет
уравнению ![]() и
граничным условиям
и
граничным условиям ![]() ,
,![]() .
Эти условия порождают систему для нахождения
.
Эти условия порождают систему для нахождения ![]() ,
имеющую вид
,
имеющую вид
![]() ,
(
,
(![]() ).
).
Или в моем случае:
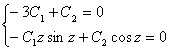 .
.
.
Равенство нулю определителя в системе приводит к уравнению
![]() ,
что в моем случае выглядит следующим образом:
,
что в моем случае выглядит следующим образом:
![]() ,
или в другом виде
,
или в другом виде
![]() ,
т.е. для моего случая
,
т.е. для моего случая ![]()
Получаем ![]() ,
значит
,
значит ![]() ищется
итерацией (метод проб):
ищется
итерацией (метод проб):
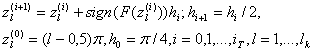 .
.
Здесь ![]() -
эмпирически подобранные и задаваемые параметры.
-
эмпирически подобранные и задаваемые параметры.
Из системы ![]() ,
(
,
(![]() )
имеем
)
имеем ![]() ,
,
![]() ,
,
![]() -
произвольный ненулевой множитель, возьмем
-
произвольный ненулевой множитель, возьмем ![]() .
.
В моей задаче ![]() ,
следовательно можно положить
,
следовательно можно положить ![]() ,
,
![]() .
.
Таким образом,
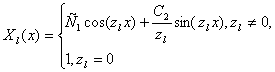 .
.
С учетом соотношения ![]() для
для
![]() находится
выражение
находится
выражение
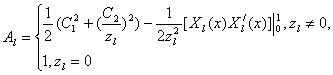
Разложим ![]() и
и
![]() в
ряд по базису
в
ряд по базису ![]() :
:
![]() ,
,
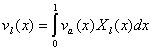 ,
,
![]() ,
,
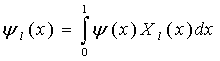 .
.
![]() и
и
![]() легко
находятся:
легко
находятся:
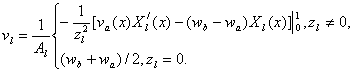
В моей задаче
![]()
Здесь ![]() ,
(
,
(![]() ),
),
![]() -
финитная функция в виде равнобедренного треугольника с высотой
-
финитная функция в виде равнобедренного треугольника с высотой ![]() ,
вершиной в точке
,
вершиной в точке![]() и
шириной полуоснования
и
шириной полуоснования ![]()
Я рассмотрела ![]() ,
,![]() ,
,![]() .Тогда
.Тогда
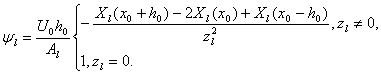
В задаче сформулированной для меня граничные условия нестационарные, правой части нет.
Пусть ![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,![]() -
заданные параметры,
-
заданные параметры, ![]() (при
всех
(при
всех ![]() )
)
Рассмотрим функцию ![]() и
ее производную по времени:
и
ее производную по времени:
![]() ;
;
![]() .
.
Введем функцию ![]() соотношением
соотношением
![]() .
.
![]() будет
решением задачи
будет
решением задачи
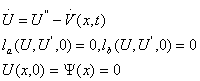 .
.
Решение этой задачи с однородным уравнением ,
то есть при ![]() ,
дается рассмотренными выше формулами
,
дается рассмотренными выше формулами
![]() ;
;
![]() ;
;
![]() .
.
.
.
Вариация произвольных постоянных ![]() с
учетом правой части уравнения дает в итоге тестовое решение:
с
учетом правой части уравнения дает в итоге тестовое решение:
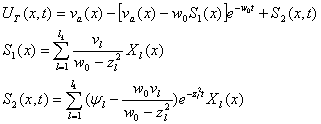 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.