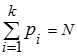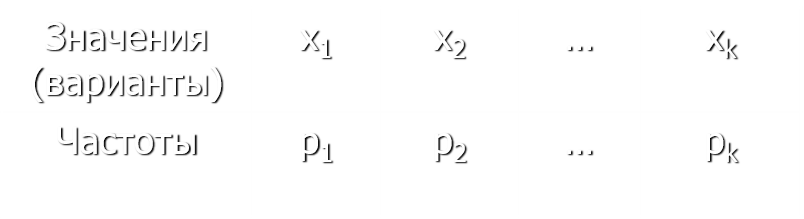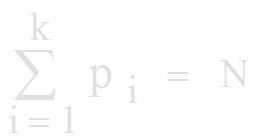Лекция 1
Описание данных Основные понятия проверки статистических гипотез
Методы статистики позволяют:
-
доказывать правильность и обоснованность используемых методов;
-
обосновывать план эксперимента;
-
обобщать данные эксперимента;
-
находить зависимости;
-
выявлять наличие различий;
-
строить статистические предсказания и др.
Пример вероятностного характера статистических выводов
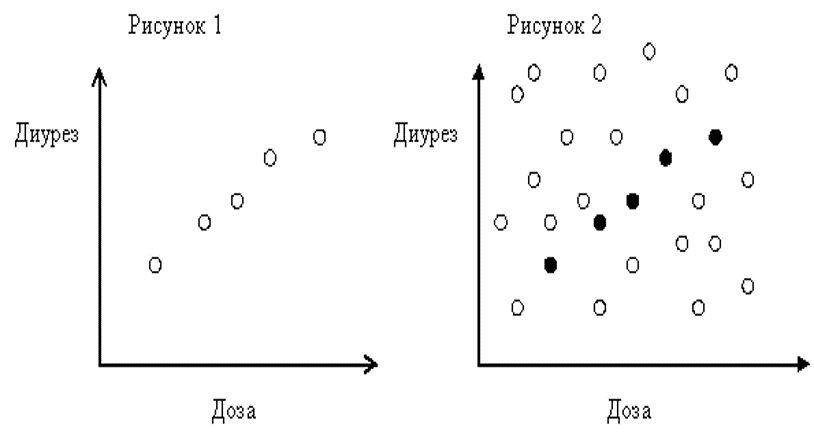
Описательная статистика
-
Распределение
-
Вариационный ряд
-
Генеральная совокупность
-
Выборка
-
Представительность выборки:
-
случайность выбора;
-
независимость результатов наблюдений;
-
правильное определение объема.
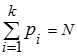
Табличное представление результатов
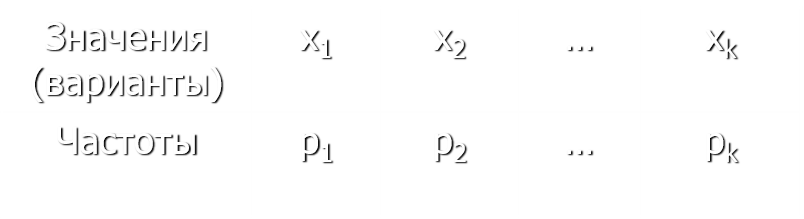
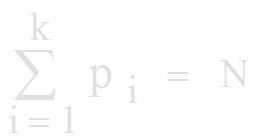
-
где N – объем выборки, k – количество вариант (k≤N).
Пример:
20 студентов получили следующие оценки по тесту:
61 62 63 63 69 72 72 76 76 77 78 78 81 83 85 85 85 86 93 97
Таблица частот

Гистограмма

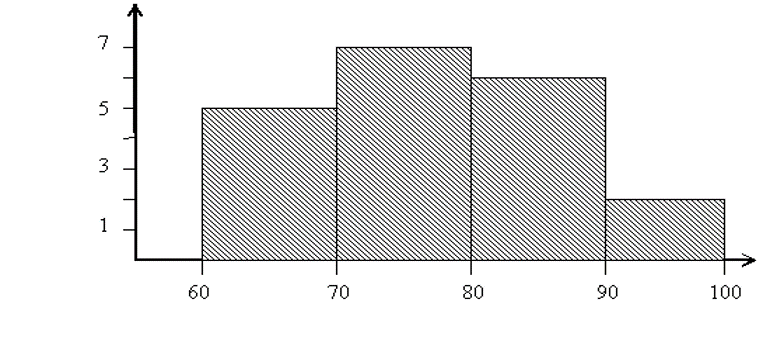
Параметры распределения
-
главная тенденция (среднее, мода, медиана)
-
разброс (дисперсия, стандартное отклонение, размах вариации, коэффициент вариации)
-
асимметрия
-
эксцесс
-
модальность
Асимметрия
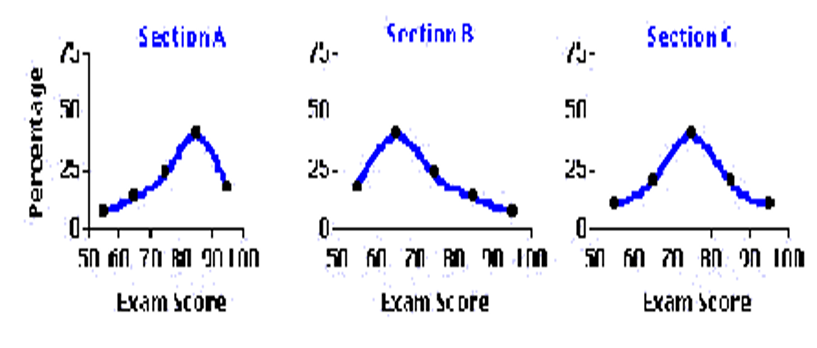
отрицательная положительная нулевая
асимметрия асимметрия асимметрия
Эксцесс, модальность
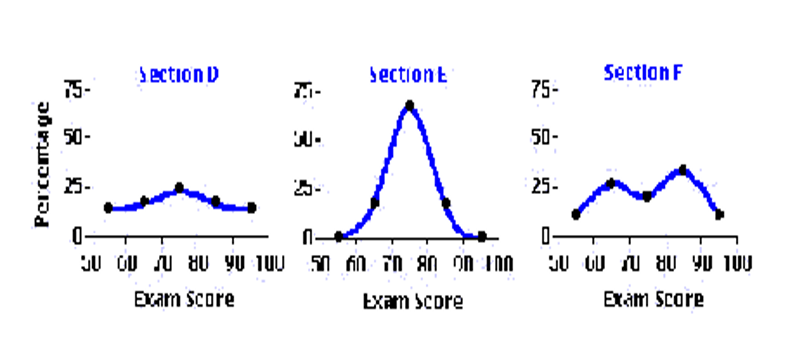
Отрицательный Положительный Бимодальное
эксцесс эксцесс распределение
Среднее значение
Сумма значений признака для всех элементов совокупности, деленная на число элементов совокупности.
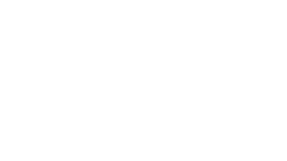
-
Медиана (Ме) – это значение признака, которое делит распределение пополам: половина значений будет больше медианы, половина – меньше.
-
Процентиль – значение признака, который делит распределение на соответствующие доли (25%, 75% и т.д.)
-
Мода (Мо) – это наиболее часто встречающееся значение признака, т.е. значение признака, наиболее характерное для данной совокупности.
Показатели разброса
-
Размах вариации – это разность между максимальным и минимальным значением признака.
-
Дисперсия - средний квадрат отклонения от среднего:
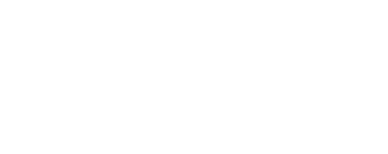
-
Стандартное (среднеквадратическое) отклонение:
-
Коэффициент вариации (в однородной совокупности не превышает 33%):
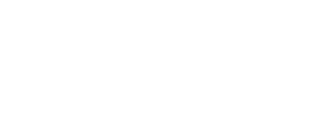
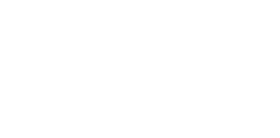
Нормальное (гауссово) распределение
-
Плотность распределения:
-
Полностью определяется:
-
средним значением μ (положение кривой распределения и место ее максимума);
-
стандартным отклонением σ (форма кривой).
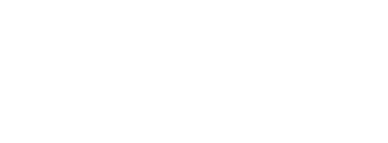
Правило «трех сигма»
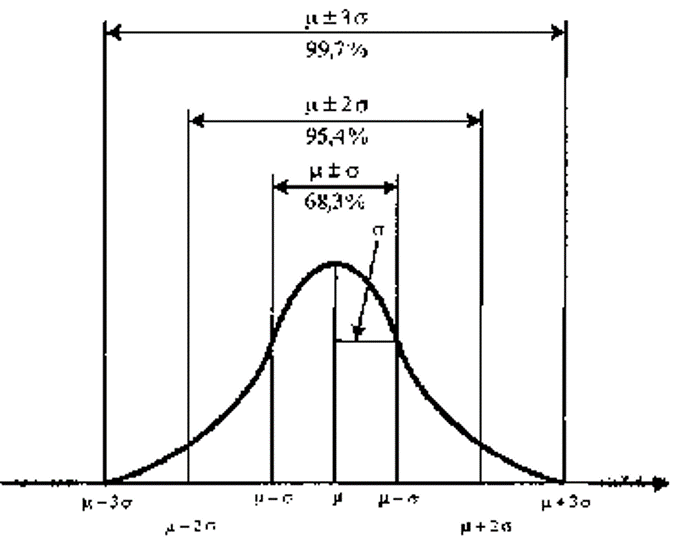
-
При отклонении распределения от нормального лучше использовать медиану, моду и процентили
-
Соответствие между процентилями и числом стандартных отклонений (для проверки распределения на нормальность:
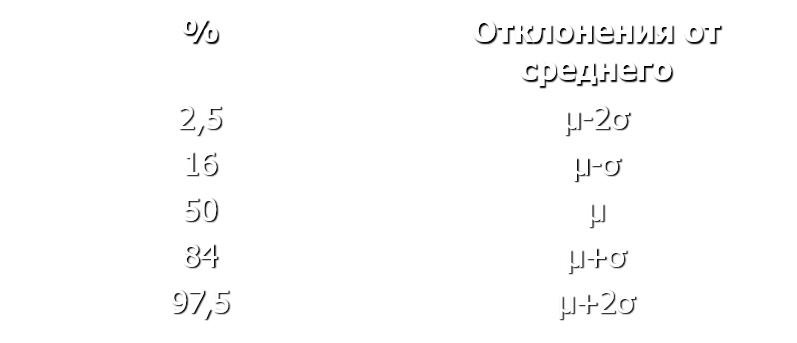
Расположение моды медианы и среднего в разных распределениях
Нормальное Положительное Отрицательное
распределение смещение смещение
Выборочные оценки параметров распределения
-
Выборочное среднее:
-
Выборочное стандартное отклонение:
-
Стандартная ошибка среднего:
Критерии значимости
-
Нулевая гипотеза (Н0): исследуемые факторы не оказывают никакого влияния на исследуемый параметр; между сравниваемыми группами нет различий
-
Альтернативная гипотеза (Н1): определяется формулировкой задачи
-
Критическая величина: получают из набора статистических таблиц
-
Проверку гипотез осуществляют на основании результатов выборки.
-
Если статистика критерия превышает критическую величину:
-
нулевая гипотеза отклоняется;
-
различия признаются статистически значимыми.
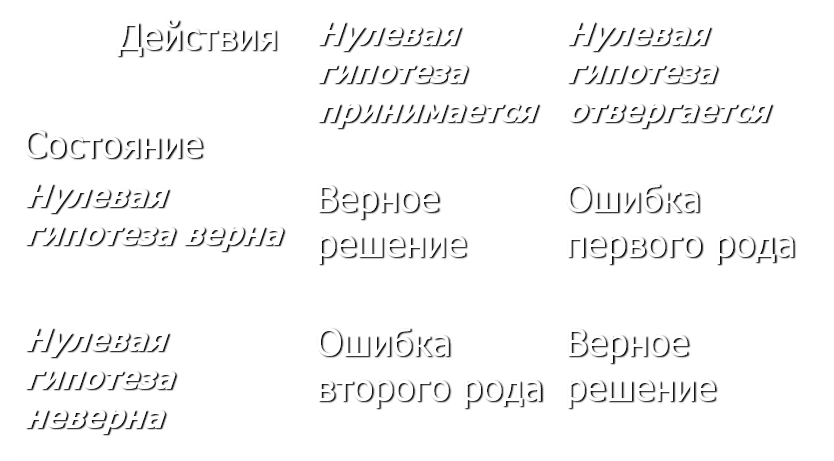
Сочетания объективного состояния гипотезы и субъективных действий:
-
Вероятность ошибки первого рода равна α - уровень значимости критерия
-
Максимальная приемлемая вероятность α=0,05
-
Вероятность ошибки второго рода равна β
-
Величина 1-β называется мощностью критерия