Лекция 2
Параметрические критерии
Критерий Стьюдента
-
Условия применения:
-
исходная совокупность имеет нормальное распределение;
-
выборки извлечены случайным и независимым образом.
Пример
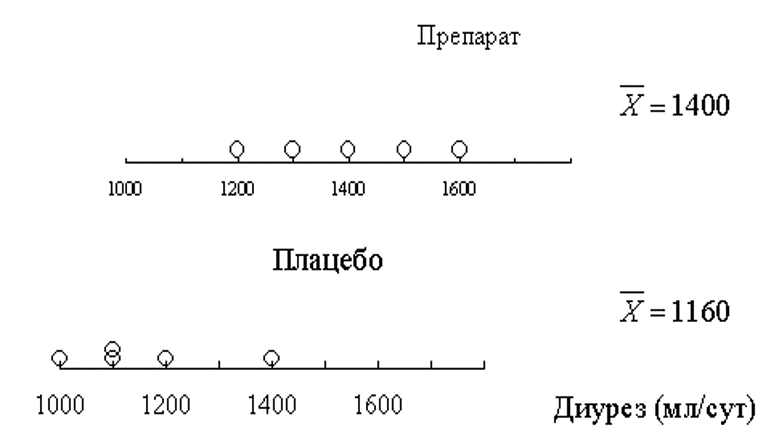
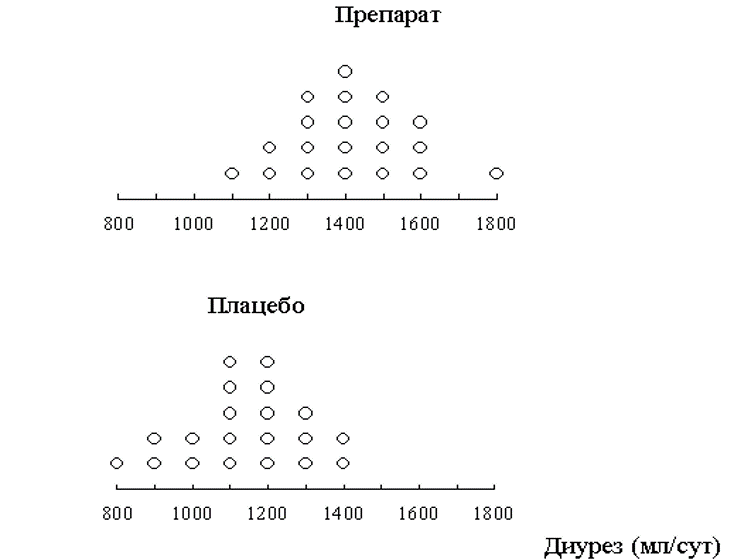
Расчет статистики критерия Стьюдента
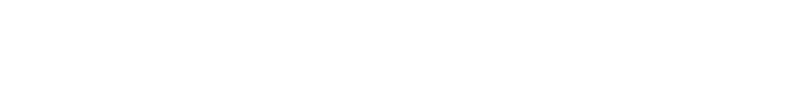
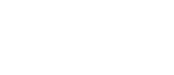
-
Разность средних:
-
Стандартная ошибка разности:
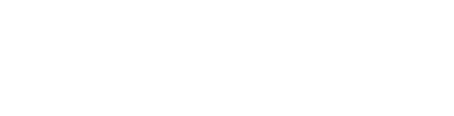
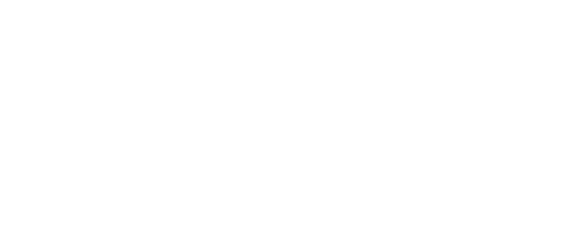
Число степеней свободы:
ν=2(n-1) (для выборок одинакового объема)
ν=n1+n2-2 (для выборок разного объема)
Объединенная оценка дисперсии
-
для выборок одинакового объема:
-
для выборок разного объема:
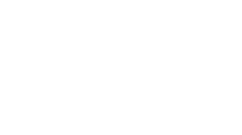
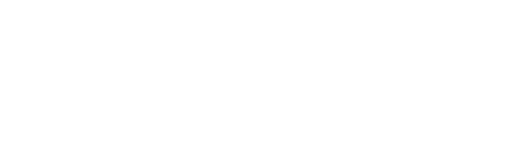
-
Двусторонний критерий:
-
средние в двух выборках не равны
-
Односторонний критерий:
-
отличия выявляются только в одну сторону
-
или
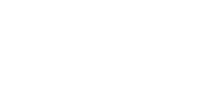
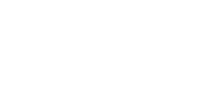
Процедура применения критерия Стьюдента:
-
вычисляем средние значения и выборочные дисперсии;
-
находим объединенную оценку дисперсии;
-
вычисляем значение t и сравниваем с критическим значением из таблицы в зависимости от числа степеней свободы и уровня значимости;
-
Если , то отвергаем нулевую гипотезу и утверждаем, что с уровнем значимости α существуют различия между двумя группами.
Пример
Средняя продолжительность госпитализации 36 больных пиелонефритом, получавших правильное (соответствующее официальным рекомендациям) лечение, составила 4,51 суток, а у 36 больных, получавших неправильное лечение – 6,28 суток. Стандартные отклонения для этих групп составили соответственно 1,98 суток и 2,54 суток. Можно ли считать эти различия случайными?
Нулевая гипотеза: группы не отличаются по продолжительности госпитализации (т.е. различия являются случайными).
Объединенная оценка дисперсии:
-
ν = 2(n–1) = 2 (36 – 1)= 70
-
для α = 0,01 и ν=70 tкрит=2,648 (по двустороннему критерию)
-
t>tкрит , значит различия в сроках госпитализации статистически значимы.
Критерий Стьюдента для множественных сравнений
-
Эффект множественных сравнений:
-
Вероятность ошибиться хотя бы в одном из попарных сравнений в общем случае равна:
-
Р=1–(1–0,05)k,
-
где k – число парных сравнений.
-
критерий Стьюдента может быть использован только для проверки гипотезы о различии средних в двух группах.
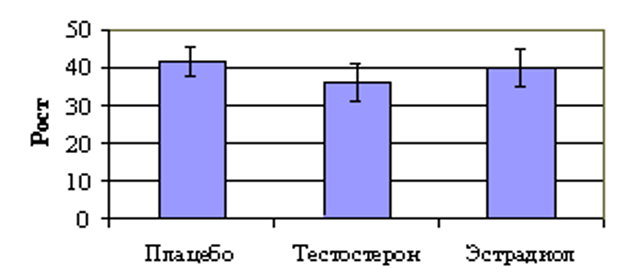
Пример Исследование влияния гормонов человека на рост марсиан
-
плацебо-тестостерон t=2,39;
-
плацебо - эстрадиол t=0,93;
-
тестостерон - эстрадиол t=1,34.
-
Число степеней свободы составляет 18, t0,05;18=2,101.
Поправка Бонферрони
-
Для обеспечения вероятности ошибки первого рода α, в каждом из сравнений необходимо принять уровень значимости α/k, где k – число попарных сравнений
-
Например: при трехкратном сравнении уровень значимости в каждом из сравнений должен быть 0,05/3≈0,017
-
При сравнении нескольких групп с контрольной уровень значимости в каждом из сравнений равен α/(m-1), где m – количество групп
Критерий Стьюдента для повторных измерений
-
Пример: гипотеза о том, что люди выше, когда они в обуви (A), чем когда они босиком (В).
-
Среднее значение в выборке А - 167,7 см (стандартное отклонение 12,03).
-
Среднее значение в выборке В – 163,7 см (стандартное отклонение 12,17).
-
Значение t = 0,89. Для α=0,05 и ν=28 критическое значение t равно 2,05.
?
-
Тест Стьюдента не в состоянии определить такой простой факт?
-
Разница между двумя группами вызвана простой случайностью?
Здесь только одна выборка D: разность между двумя измерениями
-
Среднее значение для D равно 3,93, стандартное отклонение 1,1
-
t=13,85; ν=n-1=14 – отвергаем нулевую гипотезу

Пример. Изучение суточного диуреза у 10 человек после приема препарата и у 10 после приема плацебо.

-
В первой группе среднее - 1330 мл, стандартное отклонение 353,7 мл, во второй – 1412 мл и 356,1 мл соответственно; t=0,52
-
Для разности среднее значение – 82, стандартное отклонение 97,84; t=2,65
Процедура применения критерия Стьюдента для повторных измерений
-
Условие применения: нормальное распределение разности между парами значений.
-
Вычисляем разность между значениями измерений для каждого субъекта исследования.
-
Находим среднее значение и стандартное отклонение для разности.
-
Вычисляем значение t и сравниваем с критическим значением из таблицы в зависимости от числа степеней свободы (ν=n-1) и уровня значимости.
-
Если , отвергаем нулевую гипотезу и утверждаем, что с уровнем значимости α существуют различия между двумя измерениями.
Дисперсионный анализ
-
Предназначен для сравнения двух и более групп;
-
каждая выборка независима от остальных выборок;
-
каждая выборка случайным образом извлечена из исследуемой совокупности;
-
совокупность нормально распределена;
-
дисперсии всех выборок не сильно отличаются друг от друга.
Дисперсионный анализ для групп одинаковой численности
Две оценки дисперсии совокупности
(k – количество групп, n – численность группы)
По выборочным По выборочным
дисперсиям: средним:
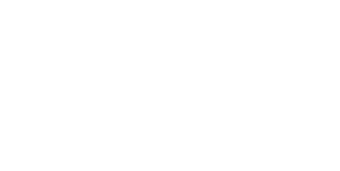
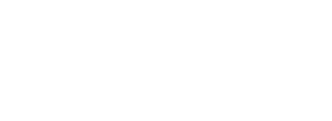
Критерий F
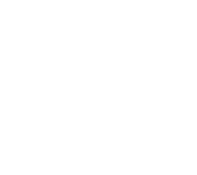
-
Межгрупповое число степеней свободы νмеж=k-1
-
Внутригрупповое число степеней свободы νвнутр=k(n-1)
-
Если рассчитанное F больше, чем табличное для соответствующего числа степеней свободы и уровня значимости, то нулевая гипотеза о равенстве выборочных средних отвергается.
Дисперсионный анализ для групп разной численности
Межгрупповая вариация
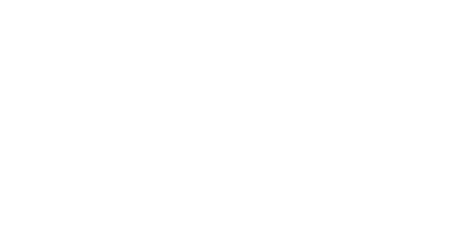
Внутригрупповая вариация
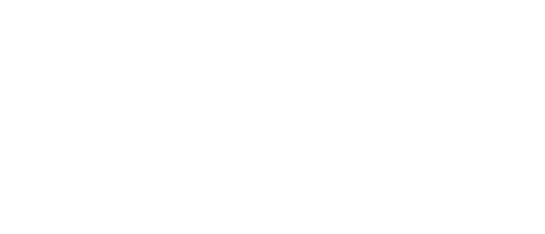
Критерий F
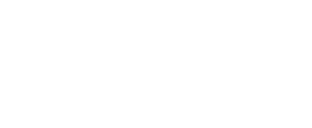
Процедура использования дисперсионного анализа
-
Вычисляем средние значения и дисперсии в каждой выборке;
-
Вычисляем внутригрупповую и межгрупповую вариации и число степеней свободы;
-
Вычисляем F;
-
Находим критическое значение F по таблице в зависимости от числа степеней свободы и уровня значимости;
-
Если рассчитанное F больше табличного, то отвергаем нулевую гипотезу о статистической значимости различий между группами.
Критерий Стьюдента с точки зрения дисперсионного анализа
-
Критерий Стьюдента является вариантом дисперсионного анализа в случае сравнения двух групп
-
F=t2
-
νмеж=k–1=2–1=1
-
νвнутр=k(n–1)=2(n–1)