Тепломассообмен 10
● Система дифференциальных уравнений конвективного теплообмена ● Условия однозначности
К дифференциальному уравнению теплопроводности в жидкости
![]()



![]()

![]()
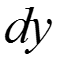
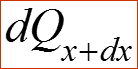
![]()
![]()

![]()
Методы математической физики
В математической физике изучают явление в бесконечно малом объеме dv за бесконечно малый промежуток времени что позволяет пренебречь величинами 2 порядка малости. Принимаются допущения: тело однородно и изотропно; физические свойства тела в малом объеме dv постоянны; внутренние источники теплоты отсутствуют. По аналогии с дифференциальным уравнением теплопровод- ности в твердом теле, которое было выведено ранее, можно получить дифференциальное уравнение теплопроводности в жидкости (уравнение энергии Фурье – Кирхгофа).
![]()
![]()
Уравнение теплового баланса
Уравнение теплового баланса: Q = Q1, (1) где Q – изменение внутренней энергии объема dv за время d ; (2) – изменение внутренней энергии объема dv за время ; Q1 – теплота, подведенная (3) конвекцией и теплопроводностью к объему dv за время . По оси х: (4)
![]()

![]()

![]()
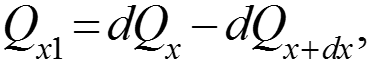
![]()
Ряд Тейлора
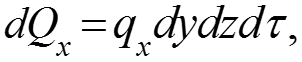
Теплота на входе вдоль оси х: (5) Теплота на выходе вдоль оси х: (6) Если функция в интервале dx непрерывна и дифференцируема, то ее можно разложить в ряд Тейлора: (7) где как величина 2 порядка малости.
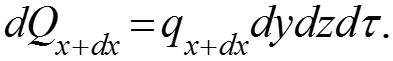
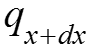

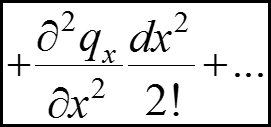
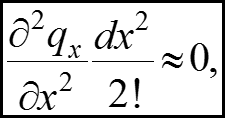
Теплота, подведенная теплопроводностью и конвекцией
Подставляя (5), (6), (7) в (4), имеем теплоту, подведенную вдоль оси х к бесконечно малому объему dv за бесконечно малый промежуток времени Аналогично (9) вдоль осей y и z: (10)
![]()
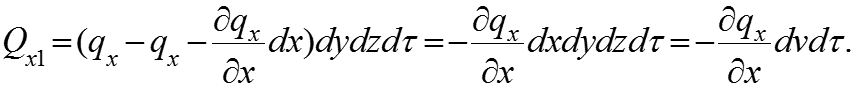
(8)
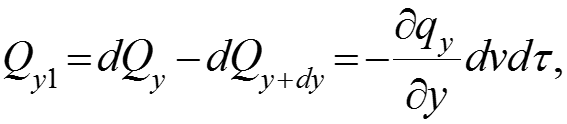
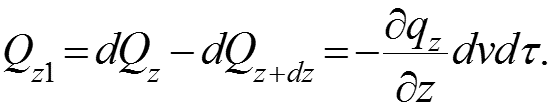
Дивергенция q
После подстановки (2), (3), (8), (9), (10) в (1) получаем: После сокращения на dv, имеем: (11) где
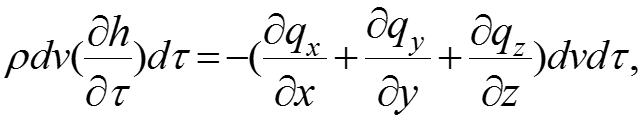
![]()
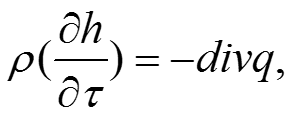
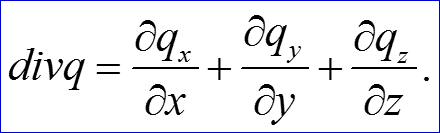
Теплота, подведенная к элементарному объему
Тогда теплота, подведенная к объему dv за время конвекцией и теплопроводностью: (12) где расход массы через единицу сечения в единицу времени, кг/(м2с). Аналогично вдоль оси y: ; и вдоль оси z: .
![]()
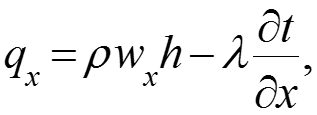
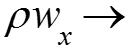
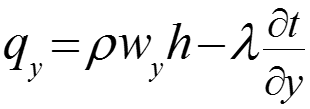
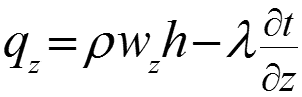
Производные
Возьмем производные по координатам х, y, z от тепловых потоков: (13) (14) (15)
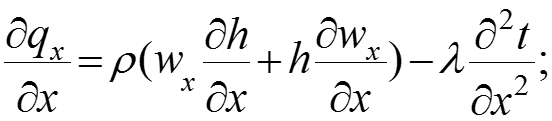
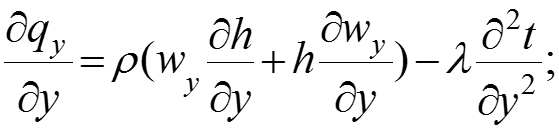
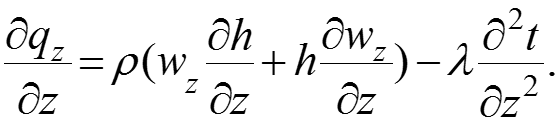
Общий вид дифференциального уравнения энергии Фурье-Кирхгофа
После подстановки (13), (14), (15) в (11) получим общий вид дифференциального уравнения энергии Фурье-Кирхгофа:
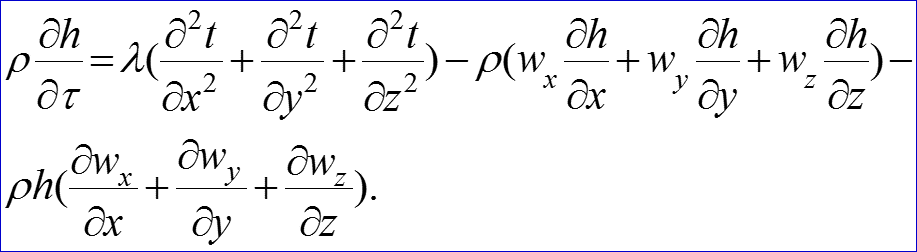
(16)
Дифференциальное уравнение сплошности
В уравнении (16) выражение (17) представляет собой дифференциальное уравнение сплошности (неразрывности) течения жидкости. Введем обозначение оператора Лапласа: . (18)
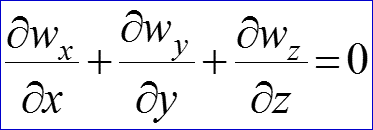

Развернутое выражение дифференциального уравнения энергии
С учетом выражений (17) и (18) уравнение энергии примет вид: (19) где энтальпия h = cpt, тогда развернутое уравнение энергии: (20)
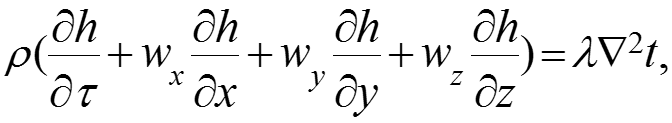

Субстанциональная производная
В уравнении (20) выражение в скобках представляет собой полную (субстанциональную) производную от температуры по времени и координатам: (21) где проекции скоростей жидкости на оси координат:

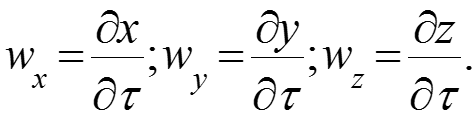
Дифференциальное уравнение энергии Фурье-Кирхгофа
После деления уравнения (20) на , с учетом (21) и обозначения коэффициента температуропроводности жидкости: получаем окончательное выражение дифференциального уравнения энергии: (22)

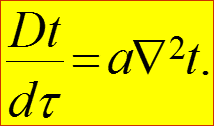
Частный случай дифференциального уравнения энергии
Частным случаем дифференциального уравнения энергии (22) для твердого тела является дифференциальное уравнение теплопроводности, которое было выведено ранее: .
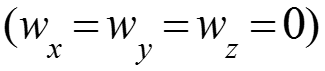

Дифференциальное уравнение движения жидкости Навье-Стокса
Вывод дифференциального уравнения движения жидкости Навье-Стокса сложен, поэтому оно приводится без вывода: (1) где оператор Гамильтона для давления: Стрелки в уравнении (1) отмечают векторные величины.
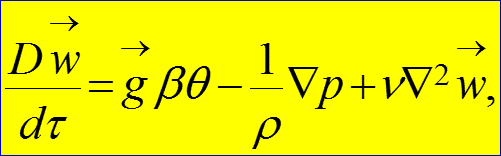
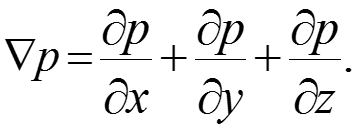
Продольное обтекание жидкостью вертикальной пластины
Невозмущенная жидкость
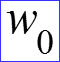
![]()
![]()
Эпюра скоростей
![]()
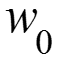
![]()
![]()
Эпюра температур
![]()
![]()
![]()
![]()
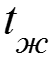
![]()
![]()
![]()
Проекции дифференциального уравнения движения на оси координат
При продольном обтекании вертикальной пластины, когда ось «х» направлена вниз, проекции ускорения на оси координат: gy = gz = 0, тогда gx = g = 9,81 м/с2 – ускорение свободного падения. В этом случае (1) проекции уравнения Навье-Стокса (1) (2) на оси координат:
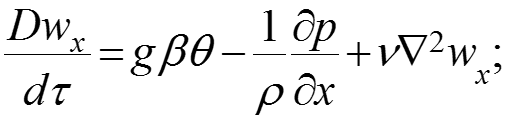
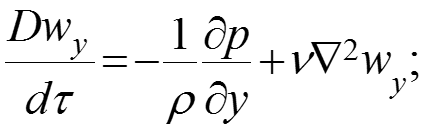
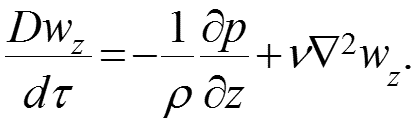
. (3)
Составляющие проекций уравнения движения на оси координат
В левых частях уравнений (2), (3), (4) находятся полные (субстанциональные) производные от скоростей по времени и координатам:
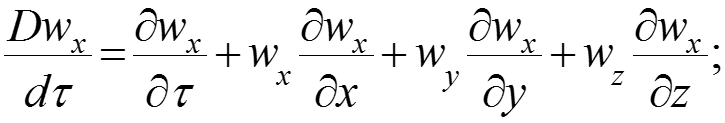
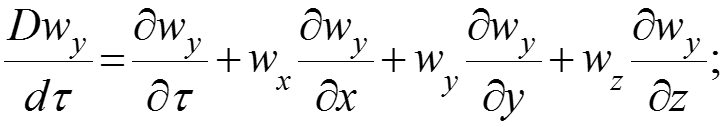
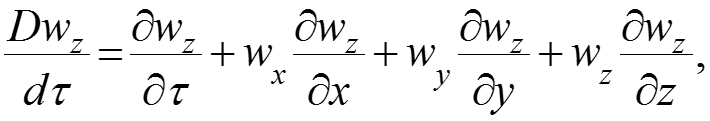
Операторы Лапласа и и уравнение неразрывности
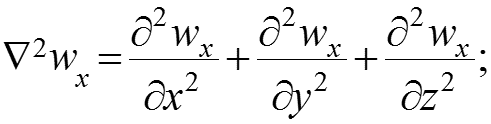
Введем обозначения операторов Лапласа: Дифференциальное уравнение сплошности (неразрывности): или в (5) векторной (6) форме:
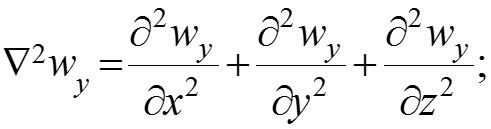

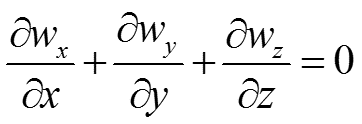

Система дифференциальных уравнений конвективного теплообмена
Итак, конвективный теплообмен описывается системой дифферен- циальных уравнений: Чтобы из бесконечного множества процессов, описываемых системой уравнений (7), выделить конкретный процесс, надо добавить условия однозначности.
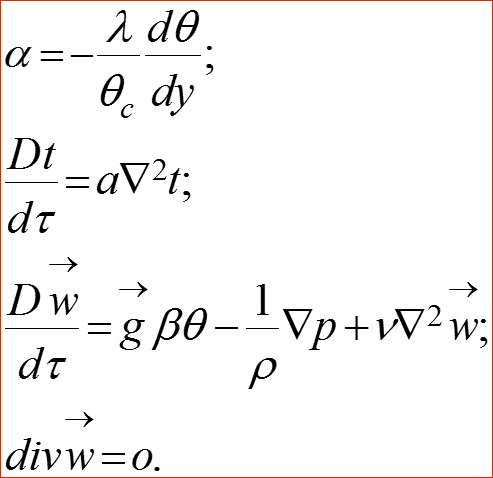
(7)
Условия однозначности
● Геометрические условия: вертикальная плоскость длиной ● Физические условия: величины постоянные, берутся при определяющей температуре. Чаще всего ей является средняя температура жидкости . ● Начальные условия: при ● Граничные условия I рода: при
![]()
![]()
![]()

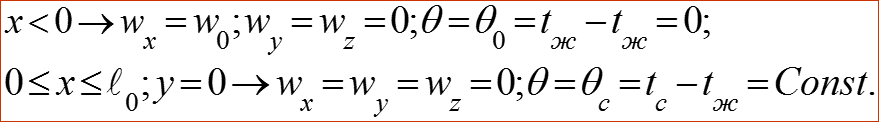
(8)
Три вида величин
В системе дифференциальных уравнений и условиях однозначности есть три вида величин: независимые переменные – постоянные величины – зависимые переменные – Общие решения системы уравнений (7) с граничными условиями
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.