Вынужденная конвекция. Условие геометрического подобия

Тепломассообмен 12

Вынужденная конвекция

Условие геометрического подобия

После проектирования и перед изготовлением энергетической установки ее работу проверяют на модели, потом делают опытный экземпляр. Чтобы можно было перенести результаты испытаний на модели на натурную установку, надо выдержать условия подобия: геометрические, физические, граничные. Для геометрического подобия модель должна быть точной копией натуры в масштабе .

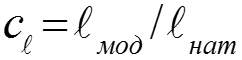
Условие физического подобия

Для физического подобия необходимо условие . Подобие граничных условий выдержать сложно, поэтому ограничиваются соблюдением условий подобия на входе жидкости в модель и натуру, то есть определяющие числа подобия на входе должны быть равными.

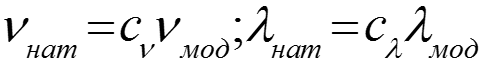
Условия моделирования процессов

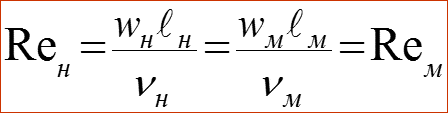
Значит скорость жидкости на входе в модель должна быть: Если жидкость одна и та же, то , то есть при . Необходимо также равенство чисел Прандтля Prм = Prн. Для разных жидкостей это трудно выдержать, например, Prвод = Prвоз при tвод = 150-300 °С, что соответствует давлению насыщения воды Pн>5 бар.

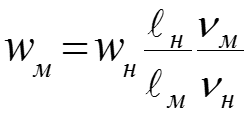
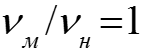
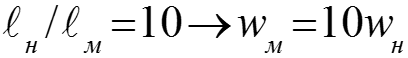
Приближенное моделирование процессов

Если учитывать еще и влияние температуры на физические свойства жидкости, то точное моделирование обеспечить сложно. Поэтому прибегают к методам приближенного моделирования, например, используют автомодельность (независимость) процесса от какого то критерия. Тогда его влияние на процесс не учитывается.

«Вырождение» числа Рейнольдса

Число Рейнольдса – это соотношение сил инерции и трения. Если одна из этих сил бесконечно велика или мала, то число Рейнольдса очень большое или очень малое, то есть происходит его «вырождение». Оно выпадает из числа определяющих критериев подобия.

«Вырождение» критерия Галилея

Например, при рассмотрении дифференциального уравнения движения Навье-Стокса мы считали жидкость несжимаемой. Из следует, что и в уравнении движения должен быть член но он был упрощен Если же не упрощать, то кроме числа Грасгофа появится еще критерий Галилея то есть при выводе уравнения движения мы считали его вырожденным.

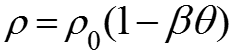
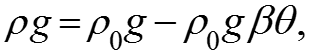
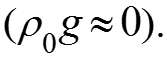
Локальное моделирование

Часто вместо точного используется локальное моделирование. Например, при поперечном обтекании трубного пучка ставится только одна рабочая трубка ( калориметр), остальные просто имитируют гидродинамику процесса. Это упрощает моделирование и дает достаточно точные результаты.

Обработка и обобщение результатов экспериментов

Во время эксперимента должны быть измерены все величины, входящие в числа подобия: тепловой поток, коэффициент теплоотдачи, температуры жидкости и стенки, скорость жидкости. При определении среднего по поверхности коэффициента теплоотдачи из уравнения подобия можно исключить координаты. Тогда зависимость примет вид: Nu = f(Re,Gr,Pr). (1)

Измерение средних температур стенки и жидкости

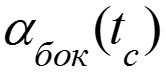
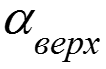
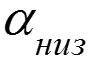
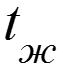
Определение средней скорости жидкости в трубе

Определение средней скорости

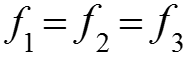
С помощью трубки Пито в равновеликих сечениях измеряются динамические напоры потока, по которым находятся скорости жидкости в этих сечениях . Тогда средняя скорость жидкости в трубе равна средне- арифметической: Для вынужденной конвекции число Грасгофа не является определяющим, то есть вместо уравнения (1) будет выражение Nu = f(Re,Pr). (2)

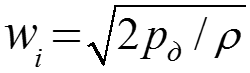
Уравнения подобия для вынужденной конвекции

Обычно это степенная зависимость (3) Для одной жидкости, без учета влияния температуры, можно считать то есть (4) или в логарифмических координатах: (5) Таким образом, выражение (5) представляет собой уравнение прямой линии (см. следующий слайд).

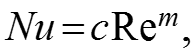
Экспериментальное определение постоянных «с» и «m»

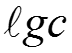
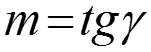
Продольное обтекание плоской поверхности

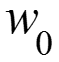
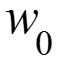
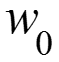
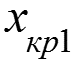
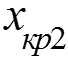
Критическое число Рейнольдса

1 – ламинарный пограничный слой; 2 – переходный режим; 3 – турбулентный пограничный слой; 4 – ламинарный подслой; 5 - невозмущенная жидкость. Обычно для простоты принимают Тогда критическое значение числа Рейнольдса для перехода от ламинарного пограничного слоя к турбулентному: (1)

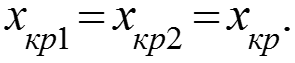
Толщина гидродинамического пограничного слоя

В ламинарном пограничном слое скорость жидкости изменяется по закону кубической параболы: (2) где толщина гидродинамического пограничного слоя: (3)

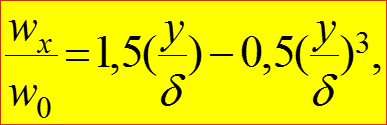
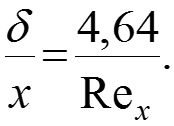
Соотношение между толщинами пограничных слоев

Внутри ламинарного пограничного слоя движение жидкости слоистое, перемешивания нет, поэтому теплота передается только теплопроводностью. В этом случае распределение температур в тепловом пограничном слое аналогично распределению скоростей в гидродинамическом пограничном слое: (4) где k – толщина теплового пограничного слоя: (5)

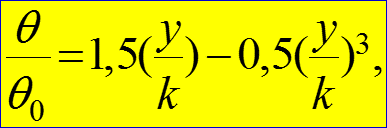
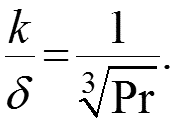
Толщина теплового пограничного слоя

Для газов Pr ≈ 1, поэтому k = δ. Подставив δ из (3) в (5), получим толщину теплового пограничного слоя: (6) При постоянной температуре плоскости локальный коэффициент теплоотдачи можно найти по уравнению подобия Михеева (7):

Уравнения подобия для теплоотдачи в ламинарном пограничном слое

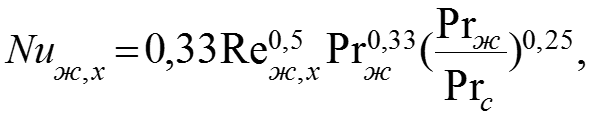
(7) где средняя температура жидкости; х – характерный линейный размер. Если температура поверхности переменная; обычно это степенная зависимость вида: (8) где А и m – постоянные, независимые от х.

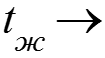
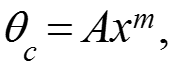
Уравнения подобия для теплоотдачи при переменной температуре стенки

Для этого случая справедливо критериальное уравнение: (9) Поправки на переменную температуру поверхности приведены на следующем слайде.

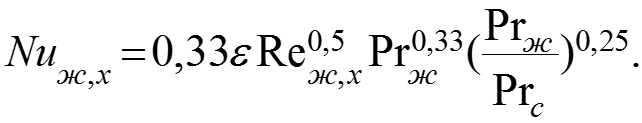
Поправки на переменную температуру стенки

К теплоотдаче от поверхности с начальным не обогреваемым участком

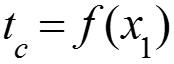
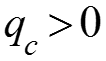
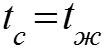
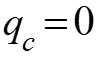
Теплоотдача от поверхности с начальным не обогреваемым участком