- перехода, поэтому процесс конденсации связан с теплообменом.
-
Различают пленочную конденсацию, когда конденсат образует
-
пленку на охлаждаемой поверхности, и капельную конденсацию,
-
когда на охлаждаемой поверхности образуются капли конденсата.
-
Коэффициент теплоотдачи выше при капельной конденсации,
-
Но в реальных теплоэнергетических установках чаще всего прихо-
-
дится иметь дело с пленочной конденсацией. Будем рассматри-
-
вать так называемую конденсацию чистого пара (т.е. без примеси
-
газов).
Конденсация пара на вертикальной стенке
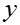

Пар
Кон-
ден-
сат

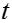



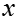
Допущения
-
Если в качестве определяющих взять среднюю скорость пара в
-
пленке, ее температуру и толщину пленки конденсата то для
-
неподвижного пара переход от ламинарного режима течения кон-
-
денсата к турбулентному происходит при критическом числе Рей-
-
нольдса Для упрощения принимаем следующие допу-
-
щения: 1) силы инерции в пленке конденсата малы по сравнению
-
с силами вязкости и тяжести; 2) учитывается только теплопровод-
-
ность и конвективный перенос поперек пленки; 3) трение на грани-
-
це пар – конденсат отсутствует; 4) температура на внешней повер-
-
хности пленки постоянна и равна температуре насыщения;
-
5) физические свойства конденсата в пленке постоянны (не зави-
-
сят от температуры); 6) плотность пара мала по сравнению с плот-
-
ностью конденсата.
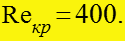
Математическое описание процесса
-
При ламинарном течении пленки конденсата перемешивания
-
нет, то есть конвекция отсутствует и теплота поперек пленки пере-
-
дается теплопроводностью. Рассматриваем стационарную задачу,
-
полагая, что высота стенки бесконечно велика, тогда процесс мож-
-
но описать системой дифференциальных уравнений энергии, дви-
-
жения, сплошности и граничными условиями:
-
при:
-
Впервые эту задачу решил Нуссельт в 1916 году и получил ура-
-
внение для среднего по поверхности коэффициента теплоотдачи.


Формула Нуссельта
-
Формула Нуссельта для конденсации неподвижного пара:
-
где константа с = 0,943, характерный линейный размер - вы-
-
сота поверхности для конденсации на вертикальной плоскости и
-
с = 0,728, - наружный диаметр трубки при конденсации на
-
горизонтальных трубах; r – скрытая теплота парообразования, Дж / кг; - плотность жидкости, ; g = 9,81 - ускорение
-
свободного падения; - коэффициент теплопроводности жид-
-
кости, Вт / мК; - коэффициент динамической вязкости жидкости,
-
- температуры насыщения и стенки,
-
Все физические свойства брать при температуре насыщения.
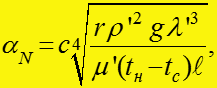
(1)


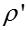
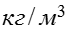
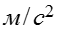
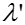
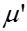
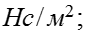
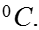
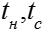
Уравнения теплоотдачи для ламинарного течения пленки конденсата
-
Формула Нуссельта дает погрешность в несколько процентов,
-
так как не учитывает зависимость физических свойств жидкости от
-
температуры и возрастание коэффициента теплоотдачи из-за вол-
-
нового течения пленки, вызванного трением на границе раздела
-
фаз. Лабунцов предложил ввести поправку на температуру в виде
-
и Капица – поправку на волновое течение
-
С учетом этих поправок средний коэффициент теплоотдачи:
-
Уравнения (1) и (2) можно представить в безразмерном виде,
-
если считать число Рейнольдса определяемым критерием подо-
-
бия
-
где - число подобия Архимеда.


(2)
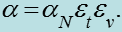

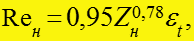
(3)

Теплоотдача при турбулентном течении пленки конденсата

-
Турбулентное течение пленки. При
-
течение в пленке становится турбулентным.
-
соответствует . Тогда критериальное уравнение
-
теплоотдачи при cмешанном течении пленки конденсата будет:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
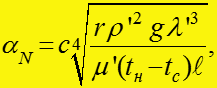
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()

