Тепломассообмен
Внутренняя задача
(практически:
![]()
![]()
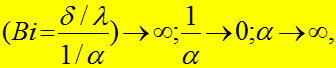
то есть очень интенсивное наружное охлаждение, поэтому температура поверхности пластины, погруженной в жидкость, сразу становится равной температуре жидкости. Распределение температур в пластине зависит от ее теплопроводности
![]()
и геометрических размеров
(внутренняя задача).
![]()
Внутренняя задача (а) Внешняя задача (б)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Внешняя задача
(практически:
![]()
![]()
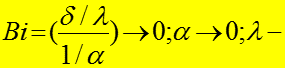
значительный.
Из-за высокого коэффициента теплопроводности пластины температуры в ней быстро выравниваются, а охлаждение слабое и все зависит от наружного коэффициента конвективной теплоотдачи
(внешняя задача).
![]()
![]()
Средний случай
![]()
Интенсивность охлаждения зависит и от внутреннего термического сопротивления и от внешнего -
![]()
![]()
Распределение температур в пластине для этого случая показано на следующем слайде. Из уравнения (13) следует, что для любого момента времени
![]()
Распределение температур имеет вид симметричной кривой с максимумом на оси пластины (Х=0). Касательные к кривым в точках проходят через точки +А и –А на расстоянии
![]()
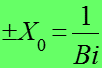
и тангенс угла наклона этих касательных:

(см. след. слайд).
![]()
Температурное поле в пластине
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Теплота, отданная пластиной при охлаждении
Теплота, отданная жидкости с обеих сторон пластины за время от до равна изменению ее внутренней энергии, Дж:
![]()
![]()
(20)
![]()
где объем пластины,
![]()
![]()
масса пластины, кг.
![]()
Тогда за любой промежуток времени от до
![]()
![]()
внутренняя энергия пластины изменится на, Дж:
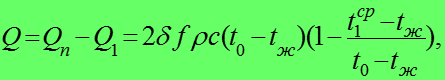
(21)
Средняя по толщине пластины безразмерная избыточная температура

(22)
где
средняя по
![]()
толщине пластины безразмерная избыточная температура в момент времени
В соответствии с «теоремой о среднем»
![]()
средняя безразмерная температура пластины найдется как:
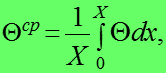
(23)
где
- по уравнению (13), тогда при можно
![]()
![]()
ограничиться только первым членом ряда, то есть:
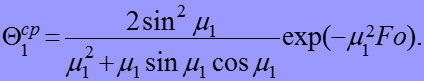
(24)
![]()
Охлаждение (нагревание) бесконечно длинного цилиндра
отдает теплоту окружающей жидкости:
![]()
при
![]()
![]()
Для бесконечного цилиндра .
При этих условиях
![]()
дифференциальное уравнение теплопроводности в полярных (цилиндрических) координатах:
Начальные и граничные условия:
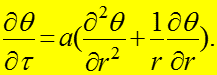

(1)
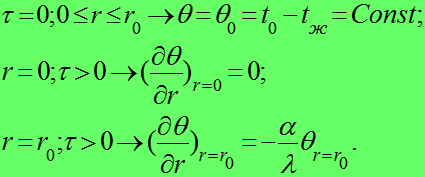
при:
(2)
Числа подобия для охлаждения (нагревания) цилиндра
(3)
![]()
где безразмерный радиус цилиндра;


число (критерий) Био, который;
представляет собой соотношение конвективной теплоотдачи снаружи и теплопроводности внутри цилиндра;

число Фурье (безразмерное время).
По аналогии с пластиной при
(практически при
![]()
![]()
степенные ряды становятся настолько быстро сходящимися, что можно ограничиться первым членом ряда
![]()
![]()
Безразмерные избыточные температуры
(4)
![]()
на поверхности цилиндра
(5)
![]()
Функции табулированы и приведены в
![]()
справочниках. По аналогии с бесконечной пластиной зависимости (4) и (5) в логарифмических координатах линейные и по ним можно найти:

или в безразмерном виде по графикам:
![]()
Теплота, отданная цилиндром окружающей жидкости
до
![]()
![]()
равна изменению внутренней энергии цилиндра, Дж:
(6)
![]()
а за время от до
(7)
![]()
![]()
![]()

где средняя по цилиндру безразмерная
При избыточная температура в момент времени
![]()
![]()
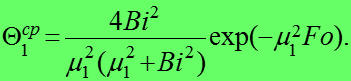
(8)
Аналогично есть решение и для охлаждения (нагревания) шара.
Регулярный режим охлаждения (нагревания) тел
было получено:
![]()
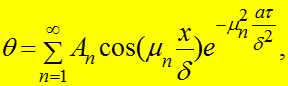
(1)
где константа для каждого члена ряда, которая
![]()
находится из начальных условий.

Множитель зависит только от координаты Х .
I – неупорядоченная стадия охлаждения

Комплекс является постоянным, положительным вещественным числом:
где
![]()
![]()
Тогда уравнение (1) запишется в виде:
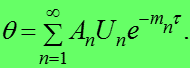
(2)
Уравнение (2) справедливо для тел разной геометрии, которая учитывается видом множителей
![]()
изменение
При малых значениях времени от до
![]()
![]()
температур зависит от начального распределения температур в теле. В этом случае поле температур будет определяться не только первым, но и последующими членами ряда (2) (I - неупорядоченная стадия процесса охлаждения).
II – я стадия охлаждения – регулярный режим
Но начиная с некоторого момента времени начальные условия
![]()
играют второстепенную роль , процесс определяется условиями охлаждения и физическими свойствами тела. Тогда температурное поле достаточно точно описывается первым членом ряда
(II – я стадия охлаждения – регулярный режим, для которого:
(3)
![]()
Логарифмируя (3) и опуская индексы, получим:
![]()
или
(4)
![]()
то есть в полулогарифмических координатах зависимость – прямолинейная.
Регулярный режим охлаждения
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
III стадия охлаждения – стационарный режим
При длительном охлаждении или
![]()
![]()
все точки тела принимают одинаковую температуру, равную температуре окружающей жидкости
(III стадия охлаждения -
![]()
стационарный режим).
Для регулярного режима после дифференцирования
уравнения (4) имеем:

(5)
то есть относительная скорость изменения температуры равняется константе «m», не зависящей от координат и времени.
m, 1/c – называется темп охлаждения.
Темп охлаждения

(6)
Зависимость темпа охлаждения от физических свойств тела, его геометрии, размеров и условий теплообмена на поверхности можно найти из теплового баланса.

(7)
Изменение внутренней энергии тела:
где средняя по объему избыточная температура.
![]()
Теплота (7) отдается от поверхности тела к жидкости:
Первая теорема Кондратьева
(8)
![]()
Здесь средняя по поверхности избыточная температура;
![]()
средний коэффициент теплоотдачи.
![]()
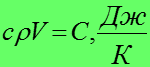
полная
Приравнивая (7) и (8) с учетом, что теплоемкость тела;
коэффициент неравномерности
![]()
распределения температуры в теле, имеем, 1/с:
то есть при темп охла-
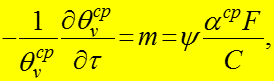
![]()
(9)
ждения однородного и изотропного тела (относительная скорость охлаждения) пропорционален коэффициенту теплоотдачи, поверхности тела и обратно пропор- ционален его теплоемкости
(первая теорема Кондратьева).
Диапазон изменения коэффициента
![]()
температуры в теле из (9):

(10)
Как же он зависит от числа Био?
А)
(практически
- внешняя задача
![]()
![]()
распределение температур не зависит от геометрических размеров тела и его физических свойств:
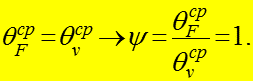
В)
(практически
- внутренняя задача
![]()
![]()
распределение температур зависит только от геометрических размеров тела и его физических свойств. Из-за высокого коэффи- циента теплоотдачи следовательно в общем
![]()
![]()
будет изменяться от до см.след.слайд!
![]()
![]()
Зависимость
![]()
![]()
![]()
![]()
![]()
Вторая теорема Кондратьева
темп охлаждения «m» тела становится
![]()
пропорциональным его коэффициенту температуропроводности
![]()
(вторая теорема Кондратьева):
(11)
![]()
Коэффициент пропорциональности «к» зависит только от
геометрии и размеров тела.

(12)
Для бесконечной пластины:
где половина толщины пластины, тогда с учетом того, что
![]()
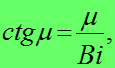
для бесконечной пластины

тогда при
Регулярные режимы I,II,III родов
(практически из (12) для
![]()
![]()
![]()


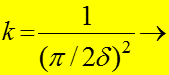
то есть откуда:
(13)
коэффициент пропорциональности для бесконечной пластины.
Есть также свои выражения для цилиндра и шара. На основе теории регулярного режима разработаны экспериментальные методы определения коэффициентов теплопроводности и температуропроводности.
При регулярный режим I рода;
при линейной
![]()
зависимости регулярный режим II рода;
при периоди-
![]()
ческой функции регулярный режим III рода,
![]()
где
- частота колебания;
- амплитуда колеб-я темп-ры жидк.
![]()
![]()
![]()
Лучистый теплообмен
технике, ядерной энергетике, металлургии, гелиотехнике и др.
Тепловое излучение – это передача внутренней энергии излучающего тела путем электромагнитных волн, которые характеризуются длиной волны
Но не все электромагнитные
![]()
волны относятся к тепловому излучению.
Тепловыми лучами являются те из них, которые при падении на поверхность превращаются в теплоту.
Таковыми являются видимое излучение (свет) с длиной волны и инфракрасное
![]()
![]()
Особенности лучистого теплообмена в разных средах
излучения, то есть испускают энергию всех длин волн от нуля до бесконечности. Но чистые металлы и газы характеризуются выборочным (селективным) излучением, то есть испускают энергию с прерывистым спектром.
В твердых и жидких телах лучистый теплообмен имеет
поверхностный характер, то есть в лучистом теплообмене участвуют лишь тонкие поверхностные слои.
Газы же имеют объемный характер лучистого теплообмена, то есть в нем принимают участие все частицы газа.
Тепловой баланс лучистого теплообмена
![]()
![]()
![]()
![]()
![]()
Тепловой баланс лучистого теплообмена в абсолютных единицах
они подчиняются законам оптики (угол падения равен углу отраже- ния), поэтому на предыдущем слайде лучистые тепловые потоки падения, отражения и пропускания соответствуют законам оптики
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.