Расчет нестационарного температурного поля однослойной вертикальной ограждающей конструкции здания методом конечных разностей при граничных условиях третьего рода

Министерство Образования Республики Беларусь

БЕЛОРУССКИЙ НАЦИОНАЛЬНАЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра “ Теплогазоснабжение и вентиляция”

Расчетно-графическая работа по тепломассообмену

РАСЧЕТ   НЕСТАЦИОНАРНОГО  ТЕМПЕРАТУРНОГО  ПОЛЯ  ОДНОСЛОЙНОЙ ВЕРТИКАЛЬНОЙ  ОГРАЖДАЮЩЕЙ  КОНСТРУКЦИИ  ЗДАНИЯ  МЕТОДОМ   КОНЕЧНЫХ РАЗНОСТЕЙ  ПРИ  ГРАНИЧНЫХ  УСЛОВИЯХ   ТРЕТЬЕГО   РОДА.

                               Выполнила: ст. гр.

                          Проверил: 

Минск- 2005.

Содержание.

1.Условие……………………………………………………………………….3

2.Физические основы расчёса………………………………………………...3

3.Методические указания……………………………………………………..9

4.Расчёты………………………………………………………………………11

РАСЧЕТ НЕСТАЦИОНАРНОГО ТЕМПЕРАТУРНОГО ПОЛЯ ОДНОСЛОЙНОЙ ВЕРТИКАЛЬНОЙ ОГРАЖДАЮЩЕЙ КОНСТРУКЦИИ ЗДАНИЯ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ ПРИ ГРАНИЧНЫХ УСЛОВИЯХ III РОДА.

1.Условие:

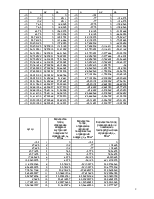
Плоская однородная однослойная стенка толщиной δ=40 мм  имеющая в начальный момент времени τ=0 одинаковую по сечению температуру  t₀= -10⁰С .С одной стороны нагревается средой , температура которой t_Ж1= 14⁰С и коэффициентом теплоотдачи α₁=8,5 Вт/(м²К), с другой стороны температура среды  t_Ж2= -24⁰С, коэффициент теплоотдачи α₂=11 Вт/(м²К).

Определить аналитическим и графическим методом температурное поле во времени, составить балансные графики теплоты во времени  с учётом теплоты, получённой от среды, температура которой t_Ж1, стенкой ,аккумулированной теплоты и теплоты, отданной среде, температура которой  t_Ж2.

Материал: ρ=1800 кг/м³

λ=0,93 Вт/(мК)

с=0,84 кДж/(кгК)

2.Физические основы расчета.

Расчет нестационарного температурного поля выполняется путем интегрирования дифференциального уравнения теплопроводности, являющегося частным случаем уравнения энергии. Последнее получено на основании закона сохранения энергии для элементарной массы и говорит о том, что разница между притоком и оттоком тепла, с учетом внутренних источников, расходуется на изменение энтальпии элементарной массы.

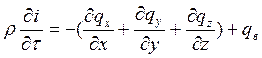                            (1)

или

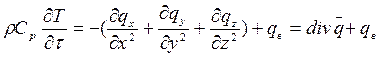             (1')

где   ρ— плотность, кг/м³;

С_p— теплоемкость при постоянном давлении, Дж/(кг*К)

τ— время, с

q_в— удельная мощность внутренних источников тепла, Вт/м³.

В общем случае тепловой поток слагается из двух составляющих:

q=q_λ+q_w                                                                               (2)

где q_λ — удельный тепловой поток за счет теплопроводности, Вт/м,

q_w — удельный тепловой поток за счет конвективного переноса, Вт/м²,

W_n— скорость среды в данном сечении, м/с;

λ— коэффициент теплопроводности, Вт/ (м*К).

При неподвижной среде q_w=O, уравнение (I) превращается в уравнение теплопроводности с внутренним источником тепла.

                                    (3)

или

                                                   (3')

Интегрирование уравнений (3) или (3') возможно лишь при наличии условий однозначности, заданных в виде функциональной зависимости от координат X, У, Z и времени τ. Совместное решение уравнения (3) с условиями однозначности позволит установить температурное поле по объему тела в любой момент времени. Однако математический аппарат, которым располагает современная наука, дает возможность решать только простейшие задачи распространения тепла с упрощенными условиями однозначности и преимущественно при одномерном тепловом потоке. Решение простейших задач и графики для вычисления температур хорошо представлены в различной литературе, но использование их не всегда представляется удобным из-за громоздкости выражений полученных решений. В таких случаях, так же как и для решения сложных задач, используют приближенные методы.

Одним из приближенных методов интегрирования дифференциальных уравнений является метод сеток или конечных разностей, который позволяет получить решение аналитически, графически или на ЭВМ.

Метод конечных разностей основан на замене производных разностными отношениями.

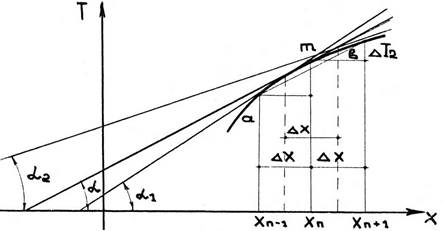
Как известно, первая производная представляет собой предел отношения приращения функции к приращению переменного ∆X при ∆X=0

Если в своем изменении аргумент не достиг 0, а равен какой-то конечной величине, то отношение приращения функции к приращению аргумента не будет производной; но чем ∆X будет меньше по величине, тем ближе отношение будет к значению производной. Поэтому, задавая значения ∆X заранее достаточно малыми, можно получить решения дифференциального уравнения с точностью, достаточной для инженерных расчетов при конечных приращениях аргумента и функции.

Рассмотрим метод конечных разностей применительно к простейшему случаю распространения тепла при одномерном тепловом потоке без внутренних источников тепла. В этом случае выражение (3) примет вид:

                                                         (4)

где a— коэффициент температуропроводности, м²/с.