Расчет нестационарного температурного поля однослойной вертикальной ограждающей конструкции здания методом конечных разностей при граничных условиях третьего рода, страница 2

Рис.1. К определению физического смысла первой и второй производной функции f(x)

Определим, как она изменится через промежуток времени ∆τ, т.е. момент τ^k⁺¹. Для этого разобьем кривую по координате X на отрезки, соответствующие слоям ∆X, настолько малые, чтобы удовлетворить требования к точности полученного результата. Обозначим через α угол, образованный касательной к кривой T^k=f(x) в точке х_п с положительным направлением оси абсцисс. Геометрический смысл первой производной представляет тангенс угла наклона касательной, в данном случае tgα. С физической точки зрения величина tgα характеризует скорость изменения данной функции, т.е. температуры в направлении X. Вторая же производная определяет интенсивность, изменения tgα в данной точке, а физически — ускорение, с которым изменяется данная функция, т.е. температура.

Точку пересечения оси слоя ∆X с кривой Т^k=f(x) обозначим через m, тогда границы слоя на рис.1 ограничены пунктирными линиями. Проведем касательные через точки пересечения пунктирных линий с кривой и найдем тангенсы углов наклона касательных в точках пересечения а и b. Заменим тангенсы касательных на их аналог, т.е. на тангенсы углов наклона секущих am и mb, что может быть с известным приближением оправдано при достаточно малых отрезках, Тогда конечно-разностный аналог второй производной представляет выражение:

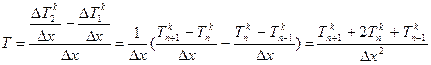
Аналогично можно показать, что для кривой первая производная будет равна:

Используя полученные выражения для первой и второй производных температур, запишем конечно-разностный аналог уравнения (4):

(5)

Решая (5) относительно T_n^k⁺¹, получим:

(6)

В уравнении (6) комплекс представляет конечно-разностный аналог критерия Фурье.

Математические разработки метода конечных разностей показали, что для возможности его реализации значение комплекса должно удовлетворять определенным условиям. То же можно показать путем сравнения приближенных данных, полученных методом конечных разностей и точными значениями, полученными на основании расчетных формул. Сравнивая, например, результаты, полученные для температур при нагревании полуограниченного тела при постоянных граничных условиях I рода по выражению:

(7)

с приближенными значениями, полученными методом сеток, можно сделать вывод, что не при любых значениях комплекса , получаются равноточные результаты. Существуют оптимальные его значения в окрестности , при которых можно получить результат с наибольшей точностью. Для инженерных же вычислений рекомендуется принимать величину . При этом результат вычислений менее точен, но зато упрощаются расчетные выражения, конечно-разностного метода. Погрешность же вычислений может быть сведена до минимума выбором достаточно малых значений ∆X

Если мы выберем интервал времени τ и толщину слоев ∆Х так, чтобы отношение , то выражение (6) примет вид:

(8)

Из него следует, что при конечно-разностном методе расчета температура n-слоя в последующий, К+1 момент времени равна средней арифметической температуре соседних слоев п+1 и п-1 в предыдущий К-тый момент времени. Эта температура может быть получена графически путем проведения отрезка прямой через точки, соответствующие температурам соседних слоев в момент времени К. Искомое значение температуры в К+1 момент времени n-слоя в точке пересечения этой прямой линии с ординатой n-слоя.

Так решается задача определения температур во времени в средних слоях любого рассматриваемого объема. Решение задачи для всего тела может быть выполнено путем ввода граничных условий.

Ввод граничных условий представляет наибольшие трудности при Решении задачи из-за наблюдающегося резкого изменения температур на границах тела в начальный момент времени. Поэтому методика ввода должна быть выбрана такой, при которой результат приближенного решения незначительно отличается от его значения при точном решении задачи. Несоблюдение этого условия приводит к грубым ошибкам.

1 2 3 4 5 6 7

Скачать файл